Производственная функция, определяющая взаимодействие факторов производства.

Производственная функция показывает функциональную связь между входными ресурсами, производственным процессом и итоговым выходом, практически решая задачу оптимизации «затраты-выпуск».

Если весь набор факторов укрупнено представить как затраты труда L и капитал К, производственная функция может быть выражена следующими образом:

Q = f(L, K)

Где Q — максимальный объем продукции, производимый при данном соотношении L и K и данной технологии.

Уравнение производственной функции данного типа показывает:

· объем выпуска зависит от количества двух групп факторов

· возможны комбинации К и L, среди которых имеется и оптимальный вариант их сочетания: (K, L) → max

· факторы можно замещать, найдя пределы замещения через соотношение отдачи цены каждого из них, получая при этом Q — const, то есть практически производственная функции дает возможность выбора рациональной технологии: трудоемкой или капиталоемкой.

График выражения функции типа Q = f(L, K) базируется на табличном ее выражении:

В данной таблице приведены данные максимального выпуска продукции при различных сочетаниях факторов производства: трудовых и капитальных затрат. Например, 85 единиц можно получить, используя две комбинации К и L (3K+1L, 1K+3L). Объем Q=120 единиц получаем, сочетая: 1K+5L, 2K+3L, 5K+1L.

Изокванта — линия равных объемов выпуска при различных сочетаниях факторов производства.

Изокванта — графическое выражение функции типа
Q = f(L, K), каждая точка которой показывает одинаковый объем и множество соотношений К и L.

Изокванта на базе данных комбинаций с Q = 120.

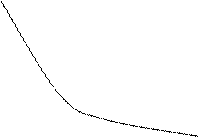
Y

5 С (5К+1L)

2 В (2К+3L)

А (1К+5L)

1 Q = 120

X