Декомпозиция элементов принципиальной схемы

1.1. Последовательный алгоритм декомпозиции

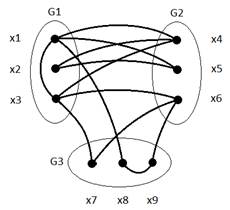
Задача: используя последовательный алгоритм распределения элементов выделить в графе G(X, U) три подграфа по три вершины в каждом, таким образом, чтобы общее число связей между подграфами было минимальным.

Исходные данные: граф G, разбитый произвольным образом на три подграфа G1, G2, G3. Каждый подграф содержит по три вершины.

На основе графа G сформируем матрицу смежности:

A(i, j) =

X1 X2 X3 X4 X5 X6 X7 X8 X9 X1                   X2                   X3                   X4                   X5                   X6                   X7                   X8                   X9                   p

Расчёты производятся по следующим формулам:

δ (xi)=p(xi)-2Σ aij, где δ (xi) – относительный вес вершины, равный приращению числа внешних рёбер формируемого подграфа, p(xi) – локальная степень вершины, aij – элемент A(I, j), где xj – вершины ранее включённые в G1.

Ход решения:

1) Выбираем вершину с минимальной степенью: p {x2, x5, x7, x8, x9} =2; поскольку кратные рёбра в данном графе отсутствуют, произвольно берём в качестве первого элемента подграфа G1 вершину x2: X(G1)={x2}.

2) Находим смежные вершины подграфа G1: Г(G1) = {x4, x5}; δ (x4) = 1, δ (x5) = 0; т.к. δ (x5) < δ (x4), добавляем вершину x5 к множеству вершин графа G1: X(G1) = {x2, x5}.

3) Находим смежные вершины G1: Г(G1) = {x1, x4}; δ (x1) = 2, δ (x4) = 1; т.к. δ (x4) < δ (x1), добавляем к G1 очередную вершину x4.

На этом формирование G1 закончено. Имеем: X(G1) = {x2, x5, x4}.

4) Из множества свободных вершин с наименьшей p {x7, x8, x9} произвольно, берём x7 в качестве первой вершины подграфа G2.

5) Находим смежные вершины X(G2): Г(G2) = {x3, x6}, δ (x3) = 2, δ (x6) = 1; т.к. δ (x6) < δ (x3), включаем в G2 вершину x6. X(G2) = {x7, x6}.

6) Находим смежные вершины G2: ГG2 = {x3, x9}, δ (x3) = 0, δ (x9) = 0. Предпочтение отдадим вершине в минимальной p. p(x9) < p(x3), добавим вершину x9 в подграф G2.

На этом формирование G2 закончено.

Имеем: X(G1) = {x6, x7, x9}.

7) В третий подграф G3 войдут все оставшиеся вершины:

Имеем: X(G2) = {x1, x3, x8}.

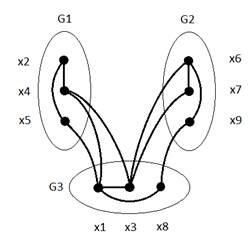
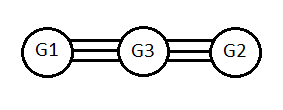
Число межмодульных связей: 6

при этом подграфы G1 и G2 не имеют непосредственных связей друг с другом.

1.2. Итерационный алгоритм декомпозиции

1. Задача: путём взаимной перестановки вершин, находящихся в разных подграфах G(X, U) добиться такого их распределения, чтобы общее число связей между подграфами было минимальным.

2. Исходные данные: граф G, разбитый произвольным образом на три подграфа G1, G2, G3. Каждый подграф содержит по три вершины.

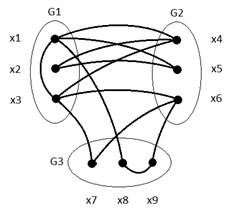
A(i, j) =

X1 X2 X3 X4 X5 X6 X7 X8 X9 X1                   X2                   X3                   X4                   X5                   X6                   X7                   X8                   X9

Расчёты производятся по следующим формулам:

Δ r_gh = (Σ a_gi - Σ a_gj) + (Σ a_hi – Σ a_hj) – 2a_gh, где

Δ r_gh – приращение числа рёбер при парном обмене вершин x_g X X_a и x_h X X_b,

Σ a_gi и Σ a_gj – число рёбер соединяющих вершину g со смежными вершинами, входящими в X_a и X\X_a соответственно.

Σ a_hi и Σ a_hj – число рёбер соединяющих вершину h со смежными вершинами, входящими в X_b и X\X_b соответственно.

a_gh – число рёбер, соединяющих вершины g и h.

Ход решения:

1. Для каждой g-ой строки матрицы A(I, j) подсчитаем (Σ a_gi - Σ a_gj) и запишем результат справа от матрицы.
2. Строим вторую матрицу той же размерности. В каждую её ячейку запишем значений приращения числа рёбер между подматрицами Δ r_gh при перестановке g-ой и h-ой вершин.
3. В полученной матрице приращений находим элемент с максимальным значением, которое характеризует на сколько уменьшится количество внешних связей между подграфами при перестановке вершин, отвечающих данным строке и столбцу.

X1 X2 X3         X1 X2 X3 X4 X5 X6 X7 X8 X9 1_2 1_3 2_3 X1                       - X2                       - X3                       - X4                     -   X5                     -   X6                     -   X7                   -     X8                   -   -1 X9                   - -1

X1 X2 X3   X1 X2 X3 X4 X5 X6 X7 X8 X9 X1               -2 -1 X2       3         -1 X3         3   -1   -1 X4               -1   X5               -1   X6                   X7                   X8                   X9

1. На первом шаге в матрице приращений имеются два максимальных значения, которые соответствуют двум возможным перестановкам: (2, 4) и (3, 5), каждая из которых уменьшит количество внешних рёбер на три.

X1 X2 X3         X1 X4 X3 X2 X5 X6 X7 X8 X9 1_2 1_3 2_3 X1                   -1 -1 - X4                   -1 -2 - X3                   -1 -1 - X2                     - -1 X5                     - -1 X6                     -   X7                   -     X8                   -   -1 X9                   - -1

X1 X2 X3   X1 X4 X3 X2 X5 X6 X7 X8 X9 X1       -1 -3     -3 -2 X4       -3 -1   -1 -2 -3 X3       -1 -1 -2 -2 -1 -2 X2               -2 -1 X5               -2 -1 X6             1 1   X7                   X8                   X9

1. Произведём перестановку строк и столбцов соответствующих вершинам 2 и 4.

1. На втором шаге в матрице приращений имеются два максимальных значения, которые соответствуют двум возможным перестановкам: (6, 7) и (6, 8), каждая из которых уменьшит количество внешних рёбер на единицу.
2. Произведём перестановку строк и столбцов соответствующих вершинам 6 и 7.
3. На третьем шаге матрица приращений не содержит положительных значений, следовательно, ни одна из последующих перестановок не приведёт к уменьшению число внешних рёбер.

1. Всего произведено две перестановки: (2, 4) и (6, 7).
2. Приведём полученный граф:

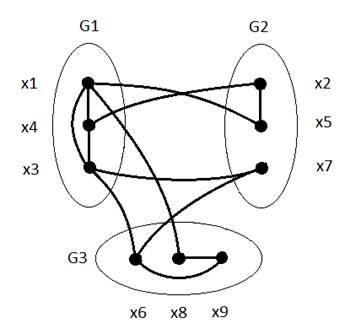
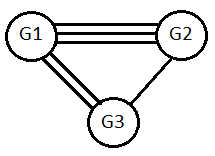
1. Применение алгоритма декомпозиции путём перестановки позволило сократить количество внешних рёбер с 10 до 6. Получили тот же результат, что и методом последовательной декомпозиции, однако в первом случае распределение связей более оптимально.