Работа 2. Оптимизация реактора идеального смешения методами нелинейного программирования

Цель работы: ознакомиться с методами нелинейного программирования. Научиться применять методы нелинейного программирования для решения задач оптимизации химико-технологических процессов.

Задание: решить задачу оптимизации реактора идеального смешения различными методами нелинейного программирования. Задача решается с помощью ЭВМ. При разработке программы использовать языки программирования Бэйсик, Паскаль по выбору студента. Для решения задачи использовать 4 метода:

1) метод наискорейшего спуска;

2) метод сканирования;

3) метод случайных направлений с обратным шагом;

4) метод “шагов по оврагу”.

Математическая формулировка задачи оптимизации часто может быть представлена как задача отыскания наибольшего или наименьшего значения функции нескольких переменных

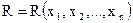(2.1)

где функция 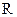является количественной оценкой представляющего интерес качества объекта оптимизации.

На независимые переменные 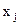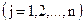в общем случае можно наложить ограничения в виде равенств:

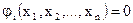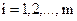, (2.2а)

или неравенств:

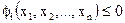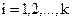, (2.2б)

или же тех и других одновременно.

Для случая, когда аналитический вид соотношений (2.1) и (2.2) известен и не слишком сложен и если, в особенности, число независимых переменных n невелико, всегда можно с бо́ льшим или меньшим успехом использовать для решения оптимальной задачи аналитические методы, по крайней мере для того, чтобы свести ее решение к решению системы конечных уравнений.

Особые трудности возникают тогда, когда соотношение (2.1), определяющее значение критерия оптимальности для заданной совокупности значений независимых переменных 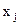, не может быть записано в явном виде. Наличие ограничений (2.2), которые могут быть заданы как трудновычислимые функции независимых переменных, еще более затрудняют отыскание оптимального решения и требует использования специальных приемов решения.

Задачи такого типа, т.е. с нелинейными и трудновычислимыми соотношениями, определяющими критерий оптимальности (2.1) и ограничения (2.2), являются предметом рассмотрения специального раздела математики – нелинейного программирования [1, 2, 5].

Как правило, решение задач нелинейного программирования могут быть найдены только численными методами, поэтому возникает необходимость применения вычислительной техники.

В большинстве своем методы нелинейного программирования могут быть охарактеризованы как многошаговые методы или методы последовательного улучшения начального решения.

Большинство методов нелинейного программирования используют идею движения в n-мерном пространстве в направлении оптимума. При этом из некоторого исходного или промежуточного состояния 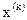осуществляется переход в следующее состояние 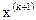изменением состояния 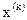на величину 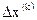, называемую шагом

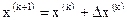. (2.3)

Очевидно, что для случая поиска минимума целевой функции 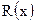должно выполняться условие

,

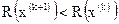иначе перевод в состояние 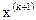нецелесообразен.

Значительное число методов нелинейного программирования в соответствии со способом определения шага 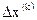можно отнести к одному из трех основных классов: