
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методика ознайомлення зі складеними арифметичними задачами.
|
|
Арифметичною задачею називають вимогу знайти числове значення деякої величини, якщо дано числові значення інших величин та існує залежність, що пов'язує ці величини як між собою, так і з шуканою величиною.
Розв'язування задачі — це процес перетворення її умови, що здійснюється на основі знань з тієї галузі, до якої належить задача, та певних загаль-нологічних правил. Цей процес складається з таких етапів: ознайомлення зі змістом задачі; аналіз задачі і складання плану розв'язування; виконання знайденого плану розв'язування; з'ясування, що здобутий результат задовольняє умову задачі (перевірка розв'язання); аналіз розв'язування (обґрунтування прийомів розв'язування, розгляд інших способів розв'язування).
Вказані етапи тією або іншою мірою характерні і для методики розв'язування задач у початкових класах. Однак здебільшого виділяють такі етапи: ознайомлення зі змістом задачі; відшукання способу розв'язування; розв'язування задачі; перевірка розв'язання і відповідь. Розгляньмо методику роботи на кожному з цих етапів.
Ознайомлення зі змістом задачі. Усвідомлення змісту задачі — необхідна умова її розв'язання. Учень не повинен приступати до розв'язування задачі, не зрозумівши її. Тому ознайомлення із задачею передбачає й опанування її змісту, і перевірку усвідомлення його дітьми.
Учень ознайомлюється із задачею зі слів учителя або самостійно. Ступінь самостійності дітей залежить від рівня їхньої підготовленості і мети розв'язування задачі. Приступаючи до розв'язування задачі, важливо сприйняти її загалом, а потім вже розбивати на окремі частини.
При фронтальному ознайомленні вчитель читає або переказує задачу двічі. Першого разу читають з метою ознайомлення зі змістом загалом.
Другого разу читають частинами і так, щоб кожна з них містила певну змістову " одиницю" тексту. Поділ задачі на частини здебільшого передбачає виділення її окремих числових даних. Під час другого читання нових задач доцільно на дошці виконувати їх короткий запис.
Читаючи задачу, вчитель паузами та інтонацією виділяє числові дані, слова, що визначають вибір дії, та запитання задачі. Емоційне забарвлення голосу допомагає учням уявити ту життєву ситуацію, про яку йдеться в задачі. Тому, слухаючи задачу, дітям не варто стежити очима за текстом підручника. Якщо в задачі трапляються маловідомі їм терміни, то їх слід пояснити заздалегідь.
Щоб перевірити, як учні усвідомлюють умову задачі, вчитель задає їм запитання (за змістом окремих частин) або пропонує переказати всю задачу. З метою активізації' контрольного повторення задачі варто іноді наперед ставити перед учнями те або інше завдання. Наприклад: " Послухайте задачу і повторіть вголос її запитання", " Прочитайте задачу самостійно і скажіть, що нам відомо про...". Розглянуті вимоги стосуються і самостійного читання задач учнями.
Підготовча робота до введення складених задач. На уроках ознайомлення зі складеними задачами важливо, щоб учні зрозуміли їхню основну відмінність від простих: ці задачі не можна розв'язати відразу, однією дією. Щоб відповісти на запитання задачі, спочатку знаходять число, якого немає в умові задачі. Розумінню цього сприяє підготовча робота, яка починається задовго до введення складених задач:
1. Розв'язування задач з недостатніми даними.
Задача. На клумбі росло 12 квіток. Декілька квіток зрізали для букета. Скільки квіток залишилося на клумбі?
Виконуючи такі вправи, учні дізнаються, що не завжди можна відразу дати відповідь на запитання задачі, бо може не вистачити числових даних. В наведеній задачі їх треба підібрати, а при розв'язуванні складених задач недостатні числа треба знайти, виконавши відповідну дію над даними у задачі числами. " 2. Вироблення вмінь розв'язувати прості задачі, які входять до складеної.
3. Постановка запитань до даної умови.
Завдання. Постав запитання до умови задачі і розв'яжи задачу.
Задача. На одній полиці було 4 книжки, а на іншій — на 2 книжки більше.
Якщо учень поставить запитання: " Скільки всього книжок на двох полицях? ", то вчитель з'ясовує, що треба знати для того, щоб відповісти на це запитання і чи відомо це з умови задачі. Вчитель підсумовує, що для відповіді на таке запитання необхідно виконати дві дії, тому для того, щоб отримати відповідь відразу, це запитання ставити не можна.
4. Розв'язування задач з двома запитаннями.
Задача. Катруся засушила 7 дубових листків, а кленових — на 2 менше.
а) Скільки кленових листків засушила Катруся?
б) Скільки всього листків засушила дівчинка?
Ознайомлення зі складеною задачею. Для ознайомлення учнів зі складеною задачею доцільно взяти таку, яка розв'язується різними діями першого
Методика викладання математики в початкових класах
ступеня. Варто розпочати із задачі, що складається з простих задач на знаходження суми й остачі.
Задача. Сашко приніс 6 морквин, а Оленка — 4 морквини. 8 морквин вони віддали кролям. Скільки морквин залишилося?
Розгляньмо два способи введення складеної задачі.
І спосіб. Учитель читає задачу, а хлопчик і дівчинка виконують відповідно ті дії, про які йдеться в умові. Повторюючи задачу, вчитель записує її коротко на дошці:
Принесли — 6 м. і 4 м. Віддали — 8 м. Залишилося —?
Потім за цим записом задачу аналізують.
Сашко приніс 6 морквин, а Оленка — 4 морквини. Про що можна дізнатися за цими даними? (Скільки всього морквин принесли Сашко й Оленка). Якою дією? (Дією додавання). Якщо буде відомо, скільки всього морквин принесли діти і скільки морквин вони віддали кролям, то про що можна дізнатися? Якою дією? (Учитель записує на дошці розв'язання, залучаючи дітей до його обгрунтування).
Це є звичайний розбір складеної задачі. Однак про складену задачу діти ще не чули. Вчитель їх просто підводить до того, що в цій задачі мають бути дві дії.
II спосіб. На столі стоїть кошик і лежать 6 та 4 морквини.
— Складемо і розв'яжемо задачу про морквини. Сашко приніс 6 морквин і поклав їх у кошик. (Учитель показує 6 морквин і кладе їх у кошик). Оленка принесла 4 морквини і поклала їх у кошик. (Учитель інсценує). 8 морквин діти віддали кролям. (Учитель виймає з кошика 8 морквин). Отже, що нам відомо? Скільки морквин приніс Сашко? (6). Скільки морквин принесла Оленка? (4). Скільки морквин діти віддали кролям? (8). А що нам невідомо? (Вчитель заглядає в кошик). Скільки морквин залишилося в кошику? Це є запитання задачі. Ми склали задачу. Запишемо її коротко і повторимо зміст задачі.
Потім учитель дає час подумати над її розв'язуванням і пропонує сказати, яку отримано відповідь. Як правило, учні швидко розв'язують задачу. Після цього бесіда продовжується.
— Правильно, у кошику залишилось 2 морквини. Як ви дізналися про це? (Від числа 10 відняли 8). Звідки взялося число 10? В умові ж його не було. (До числа 6 додали 4).
Отже, ми спочатку до числа 6 додали 4. Про що дізналися цією дією? (Скільки всього морквин поклали в кошик). Що робили потім? (Від числа 10 відняли 8. Отримали 2, тобто знайшли, скільки морквин залишилось у кошику). Щоб розв'язати цю задачу, ми виконали не одну, а дві дії. Причому ми не тільки дібрали дії, а й визначили порядок їх виконання, тобто склали план розв'язування. Запишемо розв'язання: 1)6 + 4= 10(м.); 2) 10-8 = 2 (м.). 250
Учитель спочатку з'ясовує, про що дізналися в першій дії, а тоді — в другій дії.
Тут ознайомлення зі складеною задачею відбувається так само, як і ознайомлення з простою задачею. Потребу у виконанні двох дій і складанні плану розв'язування учні " відкривають" самі. У цьому й полягає перевага другого способу.
Розвиток уявлень учнів про структуру задачі. У процесі розв'язування простих задач та ознайомлення зі складеною задачею діти отримують деякі уявлення про структуру задачі. Подальший розвиток цього уявлення відбувається під час розв'язування різних видів складених задач.
Учителі пропонують деякі спеціальні запитання і завдання, проте вони здебільшого зводяться до вимоги розчленувати задачу на умову й запитання: повторення умови задачі, її запитання; читання задачі і виділення в ній запитання; читання умови задачі про себе, а вголос — тільки запитання; визначення, що в задачі відомо, а що невідомо.
Щоб звернути увагу на основну відмінність складеної задачі від простої, ставлять, наприклад, такі запитання: Чи можна розв'язати задачу однією дією? Чому не можна розв'язати задачу однією дією? Яку маємо задачу — просту чи складену?
Такі запитання корисні, але вони не охоплюють усіх компонентів поняття " задача". Роботу в цьому напрямку потрібно урізноманітнити.
Розгляньмо питання про кількість числових даних.
Учні швидко усвідомлюють, що в арифметичній задачі має бути не менше, ніж два числа. Проте іноді вони забувають про це і намагаються розв'язати задачу тільки з одним числовим даним. З цією метою доцільно також розглядати задачі з недостатньою кількістю даних.
Задача 1. У дівчинки було 20 коп. Вона купила олівець. Скільки грошей залишилося у дівчинки?
Задача 2. На першому полі збирали пшеницю 7 комбайнів, на другому — комбайнів було більше, ніж на першому. Скільки всього комбайнів збирали пшеницю?
Учитель ознайомлює дітей із задачею, а потім запитує: " Чи можна розв'язати цю задачу? Чому її не можна розв'язати? Що треба ще знати, щоб знайти відповідь? Як треба доповнити задачу? ".
Задача може містити і два числа, але вони не перебувають у тому відношенні, яке передбачає запитання.
Задача. На прогулянку в ліс пішло 2 хлопчики. Один з них знайшов 5 грибів, а інший — менше. Скільки грибів знайшли хлопчики разом?
У роботі над деякими задачами можна вказати прийоми, за допомогою яких з'ясовують, що числові дані задачі перебувають у певних зв'язках, а їх вибір визначається запитаннями. Для задач, пов'язаних різницевим або кратним відношенням, ці прийоми зводяться до постановки запитання: що в задачі сказано про залежність між числами? Учні відповідають: " У задачі сказано, що друге число на 3 менше, ніж перше". До задач з пропорційними величинами ставлять узагальнені запитання: " Як за ціною і кількістю знайти вартість? "; " Про що можна дізнатись, якщо відомі шлях і швидкість? " та ін.
Певне значення для розвитку уявлень дітей про структуру задачі має " будова запитання". При цьому виділяють дві групи задач. Перша група — умова і запитання роздільні, тобто запитання виділено в окреме речення і не містить числових даних. Друга група — це задачі, в яких умова і запитання розділені не повністю, у запитанні є числові дані. Варто виконати кілька завдань на перебудову задачі, щоб запитання не містило числових даних.
Задача. У магазині було 2 рулони тканини: 40 м і 60 м. Скільки метрів тканини залишилось, якщо за день було продано 90 м?
Про що йдеться в задачі? (Про тканину). Скільки рулонів і по скільки метрів тканини у кожному? (Два рулони: 40 м і 60 м). Що відомо ще про тканину? (За день продали 90 м тканини). Що треба знайти? (Скільки метрів тканини залишилося).
Після розв'язання задачі вчитель пропонує учням прочитати запитання задачі і сказати, яка його частина належить до умови, а яка — до запитання.
У підручниках для початкових класів переважна більшість задач містить запитання зі словом " скільки", решта задач містить запитання з такими словами та виразами: " Чому дорівнює...? ", " Знайти...", " Обчислити...". Кількість цих задач з кожним наступним роком зростає, але за змістом вони належать до практичних задач. Це є однією з причин того, що вимогу задачі учні розуміють як речення, яке починається зі слова " скільки".
Щоб запобігти такому стереотипу, слід іноді перебудовувати запитання. Наприклад, замість " Скільки літрів бензину залишилося? " запитуємо: " Знайти остачу бензину", " Чому дорівнює остача бензину? ". Узагальнювала ним словом тут є " остача". Запитання " Скільки грошей учень заплатив за всю покупку? " можна перебудувати так: " Обчисліть вартість усієї покупки учня".
Запитання без слова " скільки" пропонує вчитель, а перебудоване запитання, що містить слово " скільки", формулюють учні.
Для розвитку уявлень дітей про структуру задачі дуже корисно використовувати вправи на перетворення та складання задач. Для простих задач основними вправами є добір запитання до умови або добір умови до запитання. З переходом до задачі на дві дії учням пропонують такі завдання: змінити в задачі умову або запитання так, щоб вона розв'язувалась двома діями, або, навпаки, перетворити складену задачу на просту.
У 3 класі запроваджується складання обернених задач.
При складанні обернених задач на 2 — 3 дії варто користуватися коротким записом задачі. Після того, як задачу розв'язано, вчитель закреслює одне з даних, на його місці ставить знак запитання, а на місці знака запитання записує знайдене шукане. За цим зміненим записом діти складають обернену задачу.
До інших творчих завдань належать: складання задач заданим розв'язком або за малюнком; порівняння задач; перетворення даної задачі на споріднену (в них величини пов'язані однаковою залежністю).
Розв'язування даної задачі та складання задачі, оберненої до неї, пов'язано з необхідністю ще раз розглянути залежності між величинами, але під іншим кутом зору. Це сприяє глибшому усвідомленню не тільки залежності між величинами і способу розв'язування задачі, а й її структури. 252
Прийоми розвитку уявлень учнів про процес розв'язування задач. Розвиток уявлень учнів про " технологію" розв'язування задач і формування вмінь розв'язувати задачі становлять фактично єдиний процес. Проте серед прийомів, спрямованих на забезпечення цього процесу, можна виділити такі, які більше стосуються його першої частини. Це розв'язування складених задач за даним планом, графічне зображення повного аналізу і плану розв'язування.
Розв'язування задач за даним планом слід розглядати і як спеціальне завдання, і як методичний прийом, завдяки чому забезпечується усвідомлення учнів у необхідності складати план, а також розкривається " технологія" розв'язування складеної задачі, її структура.
У 2-4 класах бажано розв'язати за даним планом хоча б одну задачу на тиждень.
Повний аналіз і його графічне зображення.
Задача. Купили 40 кг помідорів. Восьму частину маси усіх помідорів залишили для їжі, а решту — зас'олили порівну в 7 банок. Скільки кілограмів помідорів поклали в кожну банку?
Що треба знати, щоб відповісти на запитання задачі? (Треба знати, скільки банок було і скільки кілограмів помідорів засолили). Скільки банок було — відомо, а скільки кілограмів помідорів засолили — невідомо. Що треба знати, щоб знайти, скільки всього засолили помідорів? (Треба знати, скільки кілограмів помідорів купили і скільки залишили для їжі). Скільки кілограмів помідорів купили — відомо, а скільки залишили для їжі — невідомо. Що треба знати, щоб знайти, скільки кілограмів помідорів залишили для їжі? (Треба знати, скільки всього кілограмів помідорів купили і яку частину їх залишили для їжі. Обидві величини відомі).
Повний аналіз задачі графічно зображено на мал. 125.
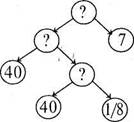
Мол. 125 Мал. 126
Кружечки зі знаком запитання позначають головне і проміжні запитання задачі. Від кожного з них проведено дві стрілки. В кінці стрілок у кружечках записують числа (відомі або невідомі), необхідні для знаходження відповіді на запитання.
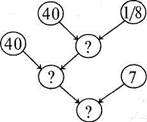
Зауважимо, що при відшуканні способу розв'язування від числових даних до запитання графічне зображення буде мати такий вигляд, як показано на малюнку (мал. 126). Відповідно до проведеного аналізу план розв'язування задачі буде такий:
План розв'язування
1) Скільки кілограмів помідорів залишилося для їжі?
2) Скільки кілограмів помідорів засолили в банках?
3) Скільки кілограмів помідорів поклали в кожну банку?
Способом повного аналізу задачі з його графічним зображенням доцільно розв'язати три-чотири задачі в 3-4 класах. Вся робота виконується під керівництвом учителя. Для самостійної роботи молодшим школярам такі завдання не пропонують.
Розгляньмо початкове ознайомлення учнів зі способом повного аналізу задачі з його графічним зображенням (мал. 127).
Задача. Посадили 6 саджанців яблунь і 2 ряди саджанців груш по 12 саджанців кожен. Скільки саджанців дерев посадили?
Бесіда. Проведемо відшукання способу розв'язування задачі. Що запитується в задачі? (Скільки дерев посадили?). Позначимо запитання відповідним знаком і візьмемо його в кружечок (мал. 127). Що треба знати, щоб знайти кількість саджанців дерев? (Треба знати, скільки посадили саджанців яблунь і груш окремо).
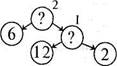
Мал. 127
Учитель проводить від цього кружечка дві стрілки і до кожної стрілки креслить по кружечку, а потім запитує:
— Чи знаємо скільки саджанців яблунь посадили? (6). Запишемо це у лівому кружечку. Чи відомо, скільки саджанців груш посадили? (Ні). Поставимо в правому кружечку знак запитання. Що треба знати, щоб знайти, скільки саджанців груш посадили? (Скільки рядів груш посадили і по скільки саджанців груш садили в ряду).
Учитель від правого кружечка проводить дві стрілки і креслить два кружечки.
— Чи знаємо, скільки рядів саджанців груш? (2). Скільки саджанців груш садили в ряд? (12). Запишемо в кружечки числа 12 і 2. Тепер можна скласти план розв'язування задачі. Спочатку дізнаємося, скільки саджанців груш посадили в 2 ряди. Це перше запитання (учитель ставить цифру 1 біля відповідного кружечка). Потім дізнаємося, скільки всього дерев посадили. Це друге й останнє запитання задачі. Отже, щоб розв'язати складену задачу, потрібно її розкласти на прості задачі і до кожної знайти відповідь.