апреля 2012 года

Томский государственный университет

Областная олимпиада по математике

апреля 2012 года

(Первый курс)

1. Существуют ли матрицы A и B размера 3´ 3 такие, что det(A + B) > |det(A)| + |det(B)|? (Через det(A) обозначен определитель матрицы A.)

Решение. Нетрудно подобрать пример, для которого требуемое неравенство будет выполнено; например, можно взять и .

2. Верно ли, что число делится на 35 при каждом натуральном n? Ответ обоснуйте.

Решение. Запишем

. Методом математической индукции можно доказать, что делится на 5, делится на 7 и, значит, делится на 35 при каждом натуральном n. (Делимость соответствующих выражений на 5 и 7 можно установить также перебором различных остатков от деления числа n на 5 и 7.)

3. Найдите все основания логарифма, при которых существуют числа, равные своему логарифму.

Решение. Должно выполняться равенство , то есть . Выясним, какие значения может принимать функция при :

.

Равенство справедливо при , т.е. имеется одна критическая точка: . Знаки производной: при , при . Значит, в точке функция имеет максимум . Это значение является наибольшим значением функции на множестве , так как

,

т.е. эскиз графика имеет следующий вид:

Таким образом, множество значений функции есть . Именно при таких основаниях логарифма (т.е. ) существует число, равное своему логарифму.

Ответ: .

4. Равносторонние треугольники со сторонами 1, 3, 5, … выстроены в ряд так, что их основания расположены на одной прямой и вплотную примыкают друг к другу. Докажите, что все вершины треугольников, противолежащие основаниям, лежат на некоторой параболе.

Решение. Введём на плоскости прямоугольную систему координат, выбрав за ось Ox прямую, на которой расположены основания равносторонних треугольников, а ось Oy направим так, чтобы она проходила через вершину первого треугольника, противолежащую основанию. Вершина n -го треугольника, противолежащая основанию, будет находиться в точке с координатами . Исключая n, найдём соотношение между координатами вершин. Оно имеет вид , а это уравнение параболы.

5. Решите уравнение .

Решение. Данное уравнение есть уравнение вида

,

где . Если есть корень уравнения , то есть , то является и корнем уравнения .

Решаем 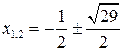. Таким образом, многочлен

делится без остатка на

. После деления получаем . Последние два корня находятся из уравнения ; .

6. Найти непрерывную на функцию такую, что .

Решение. Запишем , где — некоторое число. Согласно условию имеем =

.

Далее, .

Итак, получили функцию 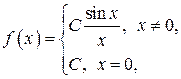непрерывную на .

7. Доказать, что если m — положительное целое число, то .

Решение. Воспользуемся тригонометрическим тождеством

т.е.

Положим ; преобразуем первый интеграл к виду

Первое слагаемое в правой части равно 0. Полагая последовательно , мы после m -кратного повторения аналогичного преобразования сведём исходный интеграл к , что и требовалось.