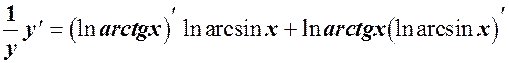До задачі 3.

Вказівки до розв’язування задач

Типового варіанту

До задачі 1

Варіант 0.

Число x = -1 - корінь чисельника і знаменника. Щоб усунути невизначеність необхідно чисельник і знаменник розкласти на множники. Для квадратного тричлена відомо, що

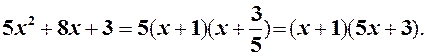
Многочлен ділиться на різницю

Тому маємо

Визначити старші члени в чисельнику та знаменнику. Відп.:

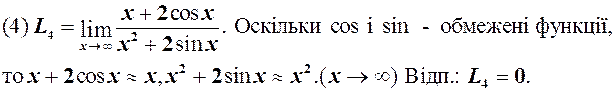
Маємо невизначеність

Перетворивши за допомогою тотожності Далі необхідно користати- ся еквівалентними Відп.:

До задачі 2

Розв’язання. Функція 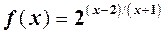не існує в точці x ₀ = - 1. Легко з’ясувати, що (x - 2)/(x + 1) — додатня н. в. при а при — від’ємна н. в. Тому

Оскільки f (x) неперервна (при x < -1 і при x > -1) і , то Ескіз графіка див. на рис.

До задачі 3.

Варіант 0.

Розв’язання. Похідною алгебраїчної суми функцій є алгебраїчна сума похідних, тобто:

Використовуючи правило диференціювання добутку двох функцій та формули знаходимо:

Після скорочення і розкриття дужок остаточно отримуємо:

2.

Розв’язання. За правилом диференціювання маємо:

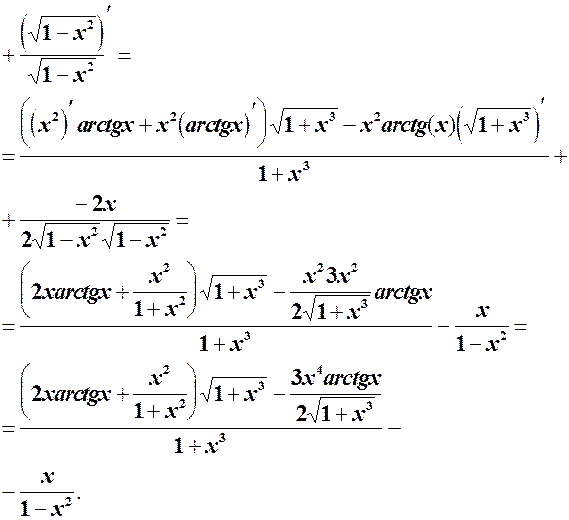
3.

Розв’язання. Для знаходження похідної скористуємось правилом логарифмічного диференціювання.

Спочатку прологарифмуємо функцію за натуральним логарифмом:

Тому що ln y - складна функція, то