Закон больших чисел

Пусть 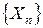- последовательность попарно независимых одинаково распределенных СВ, имеющих конечные математические ожидания 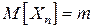и дисперсии 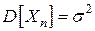, 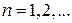Тогда при 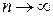среднее арифметическое 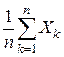сходится по вероятности к математическому ожиданию 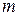, т.е. 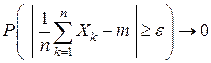при .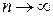

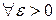Док-во. Обозначим 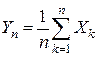, тогда по свойствам математического ожидания ( 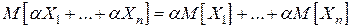для любых СВ) получим, что .

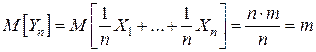Для попарно независимых СВ применим свойство сложения дисперсий (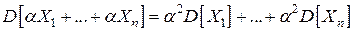) и получим, что

.

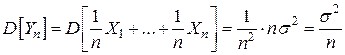В силу неравенства Чебышева

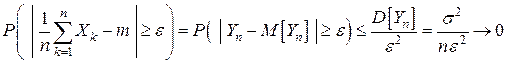при .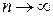

Эта теорема служит обоснованием «правила среднего арифметического» в теории измерений, в соответствии с которым за приближенное значение измеряемой величины 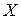следует принять среднее арифметическое ее измерений 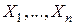. Получаемая при этом точность приближения равна 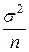, что в 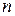раз выше, чем при использовании одного измерения.