Закон больших чисел.

Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика А.Н.Колмогорова, совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.

Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.

Лемма Чебышева. Если случайная величина принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного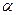

. (1)

Отсюда

(1₀)

Неравенство Чебышева. Если случайная величина имеет конечную дисперсию и математическое ожидание 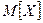, то для положительного 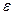справедливо неравенство

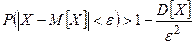(2)

Отсюда

(2₀)

Теорема Чебышева. Если - последовательность независимых случайных величин с математическими ожиданиями и дисперсиями 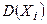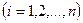, ограниченными одной и той же постоянной , то для любого положительного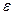

.

При доказательстве теоремы Чебышева получаем оценку

(3)

Следствие 1.( Теорема Чебышева для одинаково распределенных случайных величин). Если в условии теоремы Чебышева случайные величины имеют одно и то же математическое ожидание , то

.

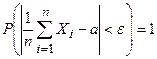Из (3) получаем оценку

(4)

Следствие 2. (Теорема Бернулли). Если в каждом из 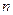независимых испытаний вероятность появления события постоянна, то при для сколь угодно малого положительного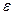

,

где - относительная частота появления события .

При доказательстве теоремы Бернулли получаем оценку

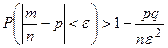(5)

Пример 1. При стрельбе по мишени, представляющей собой круг радиуса 30 см, средняя величина отклонения от центра мишени равна 6 см. Пользуясь леммой Чебышева, оценим вероятность поражения мишени при одном выстреле.

Решение. Мишень будет поражена, если произойдет событие . Средняя величина отклонения от центра мишени равна 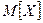. Тогда по формуле (1) получим следующую оценку:

.

Пример 2. Изготовлена партия деталей. Среднее значение детали равно 50 см, а среднее квадратическое отклонение равно 0, 2 см. Оценим снизу вероятность того, что длина наудачу взятой детали окажется не менее 49, 5 см и не более 50, 5 см.

Решение. Случайная величина - длина детали – имеет конечную дисперсию 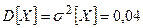и математическое ожидание . Следовательно, для оценки снизу вероятности рассматриваемого события применим неравенство Чебышева (2). Из неравенства следует , значит .

Тогда

.

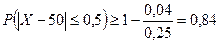Пример 3. Дисперсия каждой из 1000 независимых случайных величин равна 4. Оценим вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий по абсолютной величине не превысит 0, 2.

Решение. К последовательности рассматриваемых случайных величин можно применить теорему Чебышева, так как: 1) величины независимы, 2) дисперсии ограничены: 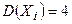, 3) математические ожидания существует. Искомую оценку получим, используя неравенство (3), где , , :

.

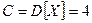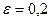Пример 4. Математическое ожидание числа очков, выпавших при подбрасывании игрального кубика, равно 3, 5, а дисперсия равна . Игральный кубик подбрасывается 350 раз. Оценим вероятность того, что среднее арифметическое числа выпавших очков отклонится от математического ожидания по абсолютной величине не более чем на 0, 2.

Решение. Случайная величина - число очков, выпавших на верхней грани игрального кубика. Эти случайные величины: 1) независимы; 2) имеют ограниченные дисперсии, 3) имеют одно и то же математическое ожидание. Искомую оценку получим, используя неравенство (4), где :

.

Пример 5. Оценим вероятность того, что в результате подбрасывания игральной кости в течение 320 раз относительная частота появления на верхней грани пяти очков отклонится от вероятности этого события (по абсолютной величине) не более чем на 0, 03.

Решение. Рассматриваемые испытания удовлетворяют схеме Бернулли: 1) испытания независимы, 2) каждое испытание имеет два исхода (на верхней грани появилось 5 очков, на верхней грани не появилось 5 очков), 3) вероятность появления 5 очков в каждом испытании постоянна и равна . Следовательно, для оценки события , где - относительная частота появления 5 очков, можно применить неравенство (5), где :

.