Краткая теория исследуемого явления. Рассмотрим наложение двух монохроматических волн, излучаемых источниками S1 и S2.

Рассмотрим наложение двух монохроматических волн, излучаемых источниками S ₁ и S ₂.

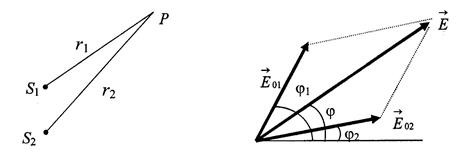
Рис. 1

Пусть значения вектора напряженности электрического поля световых волн, излучаемых источниками S ₁ и S ₂, равны

где E ₀₁, E ₀₂ – амплитуды; ω – частота; φ ₀₁, φ ₀₂ – начальные фазы колебаний;

– волновое число; r ₁, r ₂ – расстояния от источников света до точки, в которой происходит наложение лучей.

По принципу суперпозиции результирующее колебание в точке P определяется уравнением

Для нахождения амплитуды и фазы результирующей волны воспользуемся методом векторных диаграмм (рис. 1). Разность фаз двух волн

Δ φ = φ ₂ – φ ₁ = k (r ₂ – r ₁) + φ ₀₂ – φ ₀₁.

Будем считать начальные фазы волн одинаковыми.

Когерентные волны ослабляют друг друга, если разность фаз между ними равна

Δ φ = (2 m + 1)π, (m = 0, ±1, ±2,...).

Тогда можно записать равенство

cos φ ₂ = cos((2 m + 1)π + φ ₁) = –cos φ ₁.

Поэтому

E = (E ₀₁ – E ₀₂)cos·φ ₁.

Когерентные волны усиливают друг друга, если разность фаз между ними равна

Δ φ = 2 m π (m = 0, ±1, ±2,...).

Тогда

cos φ ₂ = cos2 (m π + φ ₁) = cosφ ₁,

E = (E ₀₁ + E ₀₂)cosφ ₁.

Определим, при каком условии происходит усиление когерентных волн. Выразим разность фаз через волновое число и геометрическую разность хода лучей (r ₁ – r ₂).

Усиление колебаний происходит при условии

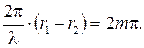
Для усиления волны оптическая разность хода лучей D должна быть равна

. (1)