
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Синхронизация генераторов, метод Хохлова
|
|
Явление затягивания частоты проявляется и во взаимной синхронизации частот двух связанных генераторов (рис. 74).
 Рис. 74. Схема двух связанных генераторов.
Рис. 74. Схема двух связанных генераторов.
|
В случае двух связанных генераторов с сильно различающимися парциальными частотами генераторы работают практически независимо, и каждый генератор генерирует свою собственную независимую моду со своей нормальной частотой близкой к парциальной. Вблизи синхронизма парциальных частот имеет место взаимная синхронизация генераторов. В полосе синхронизации в системе существуют колебания лишь одной частоты, амплитуда и фаза которых зависят от расстройки парциальных частот и от соотношения мощностей генераторов.
Колебания в связанных генераторах описываются системой приближенных уравнений

| (7.41) |
Здесь n 1 и n 2 - парциальные частоты контуров;  ;
; 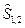 - колебательные характеристики первого и второго генераторов; a 1, a 2 - коэффициенты связи генераторов:
- колебательные характеристики первого и второго генераторов; a 1, a 2 - коэффициенты связи генераторов:
 ,
,  .
.
Будем искать синхронные решения (когда колебания установились с одной частотой), а решать будем с помощью метода ММА, тогда положим
 , ,  , ,
| (7.42) |
где w 0 = (n 1 + n 2)/2. Считая, что a и d малые параметры, запишем укороченные уравнения (3.20) в виде

| (7.43) |
где обозначено F = j - y - разность фаз колебаний генераторов; D1 = w 0 - n 1, D2 = w 0 - n 2 - расстройки генераторов;
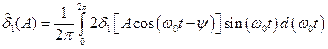 ,
,  .
.
Вычтем из четвёртого уравнения системы (7.43) второе, тогда получим, что разность фаз F удовлетворяет уравнению:
 , ,
| (7.44) |
где D = D2 - D1 = n 1 - n 2 - расстройка контуров.
Уравнение (7.44) совместно с первым и третьим уравнениями системы (7.43) образует замкнутую систему нелинейных ДУ. Для непосредственного решения эта система достаточно сложна, поэтому будем решать её методом вторичного упрощения укороченных уравнений (методом Хохлова). Для этого следует в полученной системе укороченных уравнений выделить свой малый параметр. Будем считать, что коэффициент связи генераторов достаточно мал, так что
 ,
,  .
.
В этом случае, вторые слагаемые в системе уравнении (7.43), содержащие a 1 или a 2 малы по сравнению с другими слагаемыми.
Таким образом, будем искать решение системы уравнений (7.43) с помощью разложения в ряд по малому параметру m и ограничиваясь линейными слагаемыми:
 , , 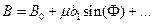 , ,
| (7.45) |
где A 0, B 0 - амплитуды колебаний в несвязанных генераторах при m = 0. Из (7.43) и определения m можно просто получить следующие условия:  . Тогда можно записать
. Тогда можно записать
 ,
,  .
.
Отсюда
 , ,  . .
| (7.46) |
В режиме синхронных колебаний система должна генерировать одну частоту w:
 .
.
Эту частоту можно найти из второго и четвёртого уравнения системы (7.43):
 . .
| (7.47) |
В синхронном и стационарном режиме разность фаз генераторов F - постоянная величина, тогда из уравнения (7.44) следует, что
 . .
| (7.48) |
Подставляя это выражение в формулы (7.45), (7.46) и (7.47), можно найти амплитуду и частоту синхронных колебаний при заданной расстройки контуров D. Естественно, что в (7.48) cos(F) по модулю не должен быть больше единицы, тогда в правой части (7.48) числитель по модулю не может стать больше знаменателя. Поэтому нетрудно видеть, что существует критическая величина расстройки D С, при которой становится невозможным синхронный режим (ширина полосы синхронного режима):
 . .
| (7.49) |
Нетрудно видеть, что если один генератор гораздо мощнее другого, то, в соответствии с формулами (7.45) и (7.46), амплитуда более мощного генератора при изменении расстройки почти не меняется. Таким образом, в данном случае мощный генератор затягивает на себя и генерирует частоту близкую к своей парциальной частоте, а маломощный генератор подстраивается под сильного соседа.
Явление затягивания используется для синхронизации генераторов, в частности, в лазерах при синхронизации мод.