
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поятие степени с рациональным показателем
|
|
Понятие корня степени N
Корнем степени n из действительного числа a, где n - натуральное число, называется такое действительное число x, n -ая степень которого равна a.
Корень степени n из числа a обозначается символом  . Согласно этому определению
. Согласно этому определению  .
.
Поятие степени с рациональным показателем
Степень с натуральным показателем: пусть а - действительное число, а n - натуральное число, большее единицы, n -й степенью числа а называют произведение n множителей, каждый из которых равен а, т.е.  . Число а - основание степени, n - показатель степени. Степень с нулевым показателем: полагают по определению, если
. Число а - основание степени, n - показатель степени. Степень с нулевым показателем: полагают по определению, если  , то
, то  . Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если
. Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если  и n - натуральное число, то
и n - натуральное число, то 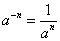 . Степень с дробным показателем: полагают по определению, если
. Степень с дробным показателем: полагают по определению, если 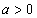 и n - натуральное число, m - целое число, то
и n - натуральное число, m - целое число, то 
2. https://ru.wikipedia.org/wiki/%D0%9B%D0%BE%D0%B3%D0%B0%D1%80%D0%B8%D1%84%D0%BC
3. Натуральный и десятичный логарифмы. Десятичным называется логарифм, основание которого равно 10. Обозначается lg b, т.е. lg b=log10 b. Натуральным называется логарифм, основание которого равно e. Обозначается ln b, т.е. ln b=loge b.
4. Из определения логарифма следует основное логарифмическое тождество[7]:

Следствие: из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений. В самом деле, если  , то
, то  , откуда, согласно основному тождеству:
, откуда, согласно основному тождеству: 
Основы тригонометрии
1.
| ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА. |
| До сих пор, говоря о тригонометрических функциях, мы считали, что аргументами этих функций являются углы или дуги. Теперь мы хотим ввести в рассмотрение тригонометрические функции числового аргумента. Такое желание вполне естественно. Когда мы говорим, например, о квадратной функции у = а х 2, то под х понимаем просто число. Это число может характеризовать время в свободном падении тел (S= gt2/2 ), сопротивление электрической цепи в законе Джоуля — Ленца (Q = IR2) и т. д. Почему же в таком случае, говоря, например, о функции у = tg x, мы под х должны понимать обязательно угол? |
| Определение. Синусом числа х называется число, равное синусу угла в х радианов. Косинусом числа х называется число, равное косинусу угла в х радианов. |
| Аналогично определяются и другие тригонометрические функции числового аргумента х. |
.
Если даны числовое множество X и правило f, позволяющее поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y = f (x) с областью определения X: y = f (x), D (f) = X.
Значения переменных, на которых задается функция y = f (x), называют допустимыми значениями переменных.
Значения переменных, при которых алгебраическое выражение P имеет смысл, называют допустимыми значениями переменных. Множество всех допустимых значений переменных называют областью допустимых значений переменных D (P).
2. https://www.habit.ru/33/165.html
Функция y = f(x) называется четной, если для любого x из области определения функции выполняется равенство
f(-x) = f(x).
Функция y = f(x) называется нечетной, если для любого x из области определения функции выполняется равенство
f(-x) = - f(x).
3. угол равный 1 радиану или, что то же самое, дуга окружности, длина которой равна радиусу этой окружности. Кроме радианной меры угла существует также градусная мера угла, которой является угол в 1 градус.
Радиан - от латинского слова radius - спица в колесе, луч. Если продумать еще раз определение угла в 1 радиан, то становится понятно, что в качестве единицы измерения в данном случае используется радиус окружности.
Формула. через пи пи= 180 гр или пи= 3, 14
|