
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка несущей способности внецентренно-сжатого внешнего простенка в осях 1-В-Г
|
|
Определение нагрузок
Выполним сбор нагрузок на простенок. Нагрузки представлены в таблицах 2.1… 3.3. Город Новосибирск находится в IV снеговом районе.
Нагрузки от совмещенной крыши приведены в таблице 2.1, от междуэтажного перекрытия – в таблице 2.2. Временные нагрузки, коэффициенты надежности по нагрузке приняты по [6].
Таблица 3.1 – Нагрузки на покрытие
| Наименование нагрузки | Нормативная нагрузка, кПа | gf | Расчетная нагрузка, кПа |
| 1.Слой изопласта марки «К» с крупнозернистой посыпкой δ =5 мм, ρ =1800 кг/м3 | 0, 09 | 1, 2 | 0, 108 |
| 2.Слой изопласта подкладочного марки «П» δ =5 мм, ρ =600 кг/м3 | 0, 03 | 1, 2 | 0, 036 |
| 3. Цементно-песчаная стяжка М-100, d=30 мм, r=1800кг/м3 | 0, 54 | 1, 3 | 0, 702 |
| 4.Керамзитобетон марки В3.5, d=200 мм, r=1400 кг/м3 | 2, 8 | 1, 3 | 3, 64 |
| 5. Железобетонная плита покрытия d=220мм | 1, 1 | 3, 3 | |
| Постоянная | 6, 46 | 7, 786 | |
| 6. Временная | 1, 678 | (0, 7)-1 | 2, 4 |
| Полная | 8, 138 | 10, 186 |
Таблица 3.2 – Нагрузки наперекрытие технического этажа
| Наименование нагрузки | Нормативная нагрузка, кПа | gf | Расчетная нагрузка, кПа |
| 1. Цементно-песчаная стяжка М-100, d=30 мм, r=1800кг/м3 | 0, 54 | 1, 3 | 0, 702 |
| 3. Утеплитель ROCKWOOLРУФ БАТТС Н, d=150 мм, r=110кг/м3 | 0, 165 | 1, 3 | 0, 2145 |
| 4. 1 слой рубероида на битумной мастике d=3 мм, r=600 кг/м3 | 0, 018 | 1, 3 | 0, 0234 |
| 5. Железобетонная плита покрытия d=220мм | 1, 1 | 3, 3 | |
| Постоянная | 3, 723 | 4, 24 | |
| 6. Временная | 0, 7 | 1, 3 | 0, 91 |
| Полная | 4, 423 | 5, 15 |
Таблица 3.3 – Нагрузки на перекрытие
| Наименование нагрузки | Нормативная нагрузка, кПа | Коэффициент надежности по нагрузке γ f | Расчетная нагрузка, кПа |
| 1.Теплоизоляционный линолеум δ =5мм, ρ =1400кг/м³ | 0, 07 | 1, 2 | 0, 084 |
| 2.Цементно-песчанная стяжка δ =30мм, ρ =1800 кг/м³ | 0, 54 | 1, 3 | 0, 702 |
| 3.Железобетонная плита перекрытия δ =220мм, ρ =2500 кг/м³ | 1, 1 | 3, 3 | |
| Постоянная | 3, 61 | 4, 086 | |
| 4.Временная | 1, 5 | 1, 3 | 1, 95 |
| Полная | 5, 11 | 6, 036 |

не читаемо. Сделай разрыв средних этажей и увеличь масштаб
Рисунок 3.1 – Поперечный разрез простенка
Проверка несущей способности внецентренно-сжатого внешнего простенка в осях 1-В-Г
Расчет элементов неармированных каменных конструкций при внецентренном сжатии производится по формуле:
N≤ mgφ RAс ω, (2.1)
где N – расчетная продольная сила, определяется по формуле 2.4;
mg – коэффициент, учитывающий влияние длительной нагрузки;
φ – коэффициент продольного изгиба, определяется по формуле 2.7;
R – расчетное сопротивление сжатию кладки, находится по таблице 2 [7];
Ас – площадь сжатой части сечения элемента, находится по формуле 2.9;
ω – коэффициент, учитывающий неравномерности в сжатой зоне, определяется по таблице 19 [7];
Расчет проводится для кирпича М125, раствор М100. Толщина стены с 1-2 этажей – 640 мм, а 3-10 этажей – 510 мм, высота – 300 см, приняты по проекту.
 =3, 47*3, 47=12, 04 м2.
=3, 47*3, 47=12, 04 м2.
Рисунок 3.2 – Грузовая площадь простенка
Определение ветровой нагрузки: оформление по гост
Расчет выполнен по нормам проектирования " СНиП 2.01.07-85* с изменением №2"
| Исходные данные | |
| Ветровой район | III |
| Нормативное значение ветрового давления | 0, 373 кН/м2 |
| Тип местности | B - городские территории, лесные массивы и другие местности, равномерно покрытые препятствиями высотой более 10 м |
| Тип сооружения | Вертикальные и отклоняющиеся от вертикальных не более чем на 15° поверхности |

| Параметры | |||
| Поверхность | Наветренная поверхность | ||
| Шаг сканирования | 3 м | ||
| Коэффициент надежности по нагрузке gf | 1, 4 | ||
| H | 33, 77 | м | |

| Высота (м) | Нормативное значение (кН/м2) | Расчетное значение (кН/м2) |
| 0, 149 | 0, 209 | |
| 0, 149 | 0, 209 | |
| 0, 158 | 0, 221 | |
| 0, 185 | 0, 259 | |
| 0, 209 | 0, 292 | |
| 0, 228 | 0, 319 | |
| 0, 245 | 0, 343 | |
| 0, 261 | 0, 365 | |
| 0, 275 | 0, 385 | |
| 0, 288 | 0, 404 | |
| 0, 301 | 0, 421 | |
| 0, 313 | 0, 438 | |
| 33, 77 | 0, 315 | 0, 442 |
Определим площадь стены Астрассчитываемого простенка:
 = bпр∙ (hзд-0, 8)-bок∙ hок∙ n=3, 47•(33, 77-0, 8)–0, 5•1, 51•2, 11•10-
= bпр∙ (hзд-0, 8)-bок∙ hок∙ n=3, 47•(33, 77-0, 8)–0, 5•1, 51•2, 11•10-
-0, 5•1, 51•1, 21•10=89, 34м2
Площадь стены на один этаж:
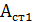 = bпр∙ (hзд-0, 8)-bок∙ hок∙ n=3, 47•3–0, 5•1, 51•2, 11-0, 5•1, 51•1, 21=7, 9м2
= bпр∙ (hзд-0, 8)-bок∙ hок∙ n=3, 47•3–0, 5•1, 51•2, 11-0, 5•1, 51•1, 21=7, 9м2
Рассчитаем полную нагрузку на простенокпервого этажа по формуле:
N=(qкрАгр+qт.э.Агр+qперАгр(n-1)+Астδ стγ кирп+Астδ утеплγ утепл
+Астδ обл.кирпγ обл.кирп)0, 95 (3.4)
 – нагрузка от совмещенной крыши, кН/м;
– нагрузка от совмещенной крыши, кН/м;
 – грузовая площадь, м2;
– грузовая площадь, м2;
qт.э - нагрузка от технического этажа, кН/м;
 – нагрузка от междуэтажного перекрытия, кН/м;
– нагрузка от междуэтажного перекрытия, кН/м;
n – количество этажей;
 – площадь стены, м2;
– площадь стены, м2;
 – толщина стены, м;
– толщина стены, м;
 – объемный вес кирпича, кН/м3;
– объемный вес кирпича, кН/м3;
0, 95 – коэффициент уровня ответственности.
N=(qкрАгр+qт.э.Агр+qперАгр(n-1)+Астδ стγ кирп)0, 9=(10, 186•12, 04+5, 15•12, 04+ +6, 036•12, 04•9+(15, 8•0.64•18+73, 54•0, 51•18)0.95= 1611кН
Рассчитаем полную нагрузку на простеноквторого этажа:
N2=(qкрАгр+qт.э.Агр+qперАгр7+Астδ стγ кирп+Астδ утеплγ утепл+ +Астδ обл.кирпγ обл.кирп)0, 9=(10, 186•12, 04+5, 15•12, 04+6, 036•12, 04•8+(7, 9•0.64•18+ +73, 54•0, 51•18))0.95=1455, 5кН
Рассчитаем полную нагрузку на простеноктретьего этажа:
N3=1300 кН
Рассчитаем полную нагрузку на простенокчетвертого этажа:
N4=1162 кН
Рассчитаем полную нагрузку на простенокпятого этажа:
N5=1024 кН
Рассчитаем полную нагрузку на простенокшестого этажа:
N6=886 кН
Рассчитаем полную нагрузку на простенокседьмого этажа:
N7=748 кН
Рассчитаем полную нагрузку на простеноквосьмого этажа:
N8=610 кН
Рассчитаем полную нагрузку на простенокдевятого этажа:
N9=472 кН
Рассчитаем полную нагрузку на простенокдесятого этажа:
N10=334 кН
Проверяю несущую способность простенка на 1-ом этаже
Для упрощения расчета разрешено рассматривать стену в пределах одного этажа как шарнирно опертую балку на двух опорах с расчетной длиной l0равной высоте этажа Н (см. рисунок 3.3)
Рисунок 3.3 – К расчету простенка
Величина изгибающего момента от этажа на уровне низа перекрытия 1-го этажа.
P=qперАгр=6, 036∙ 12, 04=72, 67 кН, (3.5)
Мэ=Р(t/2-1/3c)=72, 67(0, 64/2-1/3∙ 0, 12)=20.34кНм (3.6)
А момент на уровне низа перемычки (в расчетном сечении)
М=Мэ(Н-h1)/H=20.34(3-0.32)/3=18.17кНм, (3.7)
МW=Wm∙ 0.32=2.0461∙ 1.18=2.414кНм,
Мп=М + МW=18, 17+2.414=20, 584кНм
Наиболее опасным местом в простенке, которое и необходимо рассчитывать, является сечение, расположенное по низу перемычки, так как в этом сечении кроме продольной силы действует изгибающий момент М, который определяется от воздействия реакций перекрытия и ветровой нагрузки (рисунок3.4), расположенного непосредственно над рассчитываемым сечением 1-1.
Рисунок 3.4 – Нагрузка от перекрытия на стену
Из рисунка 3.4 видно, что давление от перекрытия на стену принимается действующим неравномерно: по внутренней грани стены максимальным и равным нулю у конца плиты перекрытия (в сечении получается треугольник). При таком распределении давления равнодействующая напряжений Р прикладывается в центре тяжести треугольника на расстоянии (t/2-1/3c) от центра тяжести стены.
В целом на расчетное сечение действуют продольная сила N и изгибающий момент Мп или, что равнозначно, продольная сила прикладывается с эксцентриситетом е0=М/N3=20, 584/1611=0.0127м. (3.8)
Несущая способность внецентренно сжатых элементов без поперечного армирования проверяется по формуле
N≤ mgφ RAс ω,
Расчетное сопротивление кладки из кирпича R находится по таблице 2 [7]. Для кирпича марки 125 и раствора марки 100: R=2, 0 МПа.
При h > 30см по [7] коэффициент mg =1.
Коэффициент продольного изгиба φ находится по формуле:
 , (3.9)
, (3.9)
где φ – коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый для расчетной высоты элемента l0 , по таблице 18 [7];
φ с – коэффициент продольного изгиба для сжатой части сечения, определяемый для фактической высоты элемента Н, по таблице 18 [7].
Гибкость элемента λ определяем по формуле:
 , (3.10)
, (3.10)
где l 0 – расчетная высота (длина) элемента;
δ ст–толщина стены.
 .
.
Гибкость сжатой части прямоугольного сечения λ с определяется по формуле:
λ c=  , (3.11)
, (3.11)
где l 0 – расчетная высота (длина) элемента, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, определяемая по формуле:
hc= δ ст -2e, (3.12)
где δ ст – толщина стены, м;
е – эксцентриситет, м.
 =δ ст–2е=0, 51 – 2·0, 0127=0, 4846 (м).
=δ ст–2е=0, 51 – 2·0, 0127=0, 4846 (м).
 .
.
По интерполяции по таблице 18 [7] находим коэффициенты φ и φ с:
φ =0, 98+(1–0, 98)  0, 9988
0, 9988
φ с=0, 95+(0, 98–0, 95)  0, 952
0, 952

Площадь сечения элемента находится по формуле:
Ас=bпрhс, (3.13)
гдеbпр– ширина простенка, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, м.
Ас=1, 81·0, 4846=0, 877 (м2)
Коэффициент ω для прямоугольного сечения вычисляют по формуле:
 (3.14)
(3.14)
где е – эксцентриситет, м;
δ ст – толщина стены, м.
ω = 1 + 0, 0127 / 0, 51 =1, 024
1, 024  – условие выполняется.
– условие выполняется.
Проверяем по формуле 2.1:
N =1611 < mgφ RAс ω = 1·0, 975·2000·0, 877·1, 024=1751 (кН)
Условие выполняется.
kз=1751/1611=1, 086
Проверяю несущую способность простенка на 2-ом этаже
Для упрощения расчета разрешено рассматривать стену в пределах одного этажа как шарнирно опертую балку на двух опорах с расчетной длиной l0равной высоте этажа Н (см. рисунок 2.5)
Рисунок 3.5 – К расчету простенка
Величина изгибающего момента от этажа на уровне низа перекрытия 2-го этажа.
P=qперАгр=6, 036∙ 12, 04=72, 67 кН,
Мэ=Р(t/2-1/3c)=72, 67(0, 64/2-1/3∙ 0, 12)=20.34кНм
А момент на уровне низа перемычки (в расчетном сечении)
М=Мэ(Н-h1)/H=20.34(3-0.32)/3=18.17кНм,
МW=Wm∙ 0.32=2.0461∙ 1.18=2.414кНм,
Мп=М + МW=18.17+2.414=19, 584кНм
Наиболее опасным местом в простенке, которое и необходимо рассчитывать, является сечение, расположенное по низу перемычки, так как в этом сечении кроме продольной силы действует изгибающий момент М, который определяется от воздействия реакций перекрытия и ветровой нагрузки (рисунок3.6), расположенного непосредственно над рассчитываемым сечением 1-1.
Рисунок 3.6 – Нагрузка от перекрытия на стену
Из рисунка 3.6 видно, что давление от перекрытия на стену принимается действующим неравномерно: по внутренней грани стены максимальным и равным нулю у конца плиты перекрытия (в сечении получается треугольник). При таком распределении давления равнодействующая напряжений Р прикладывается в центре тяжести треугольника на расстоянии (t/2-1/3c) от центра тяжести стены.
В целом на расчетное сечение действуют продольная сила N и изгибающий момент Мп или, что равнозначно, продольная сила прикладывается с эксцентриситетом е0=М/N3=19, 584/1455.5=0.0134м. (3.8)
Несущая способность внецентренно сжатых элементов без поперечного армирования проверяется по формуле
N≤ mgφ RAс ω,
Расчетное сопротивление кладки из кирпича R находится по таблице 2 [7]. Для кирпича марки 125 и раствора марки 100: R=2.0 МПа.
При h > 30см по [7] коэффициент mg =1.
Коэффициент продольного изгиба φ находится по формуле:
 , (3.9)
, (3.9)
где φ – коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый для расчетной высоты элемента l0 , по таблице 18 [7];
φ с – коэффициент продольного изгиба для сжатой части сечения, определяемый для фактической высоты элемента Н, по таблице 18 [7].
Гибкость элемента λ определяем по формуле:
 , (3.10)
, (3.10)
где l 0 – расчетная высота (длина) элемента;
δ ст–толщина стены.
 .
.
Гибкость сжатой части прямоугольного сечения λ с определяется по формуле:
λ c=  , (3.11)
, (3.11)
где l 0 – расчетная высота (длина) элемента, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, определяемая по формуле:
hc= δ ст -2e, (3.12)
где δ ст – толщина стены, м;
е – эксцентриситет, м.
 =δ ст–2е=0, 51 – 2·0, 0134=0, 4832 (м).
=δ ст–2е=0, 51 – 2·0, 0134=0, 4832 (м).
 .
.
По интерполяции по таблице 18 [7] находим коэффициенты φ и φ с:
φ =0, 98+(1–0, 98)  0, 9988
0, 9988
φ с=0, 95+(0, 98–0, 95)  0, 956
0, 956

Площадь сечения элемента находится по формуле:
Ас=bпрhс, (3.13)
гдеbпр– ширина простенка, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, м.
Ас=1, 81·0, 4832=0, 874 (м2)
Коэффициент ω для прямоугольного сечения вычисляют по формуле:
 (3.14)
(3.14)
где е – эксцентриситет, м;
δ ст – толщина стены, м.
ω = 1 + 0, 0134 / 0, 51 =1, 026
1, 026  – условие выполняется.
– условие выполняется.
Проверяем по формуле 2.1:
N =1455.5< mgφ RAс ω = 1·0, 975·2000·0, 874·1, 026=1748, 6 (кН)
Условие выполняется.
kз=1748, 6/1455, 51=1, 2
Проверяю несущую способность простенка на 3-eм этаже
Для упрощения расчета разрешено рассматривать стену в пределах одного этажа как шарнирно опертую балку на двух опорах с расчетной длиной l0равной высоте этажа Н (см. рисунок 3.7)
Рисунок 3.7 – К расчету простенка
Величина изгибающего момента от этажа на уровне низа перекрытия 3-го этажа.
P=qперАгр=6, 036∙ 12, 04=72, 67 кН,
Мэ=Р(t/2-1/3c)=72, 67(0, 51/2-1/3∙ 0, 12)=15.62кНм
А момент на уровне низа перемычки (в расчетном сечении)
М=Мэ(Н-h1)/H=15.62(3-0.32)/3=13.9кНм,
МW=Wm∙ 0.32=2.0461∙ 1.18=2.414кНм,
Мп=М + МW=13.9+2.414=16, 314кНм
Наиболее опасным местом в простенке, которое и необходимо рассчитывать, является сечение, расположенное по низу перемычки, так как в этом сечении кроме продольной силы действует изгибающий момент М, который определяется от воздействия реакций перекрытия и ветровой нагрузки (рисунок3.8), расположенного непосредственно над рассчитываемым сечением 1-1.
Рисунок 3.8 – Нагрузка от перекрытия на стену
Из рисунка 3.8 видно, что давление от перекрытия на стену принимается действующим неравномерно: по внутренней грани стены максимальным и равным нулю у конца плиты перекрытия (в сечении получается треугольник). При таком распределении давления равнодействующая напряжений Р прикладывается в центре тяжести треугольника на расстоянии (t/2-1/3c) от центра тяжести стены.
В целом на расчетное сечение действуют продольная сила N и изгибающий момент Мп или, что равнозначно, продольная сила прикладывается с эксцентриситетом е0=М/N3=16, 314/1300=0.0125м. (3.8)
Несущая способность внецентренно сжатых элементов без поперечного армирования проверяется по формуле
N≤ mgφ RAс ω,
Расчетное сопротивление кладки из кирпича R находится по таблице 2 [7]. Для кирпича марки 125 и раствора марки 100: R=2.0 МПа.
При h > 30см по [7] коэффициент mg =1.
Коэффициент продольного изгиба φ находится по формуле:
 , (3.9)
, (3.9)
где φ – коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый для расчетной высоты элемента l0 , по таблице 18 [7];
φ с – коэффициент продольного изгиба для сжатой части сечения, определяемый для фактической высоты элемента Н, по таблице 18 [7].
Гибкость элемента λ определяем по формуле:
 , (3.10)
, (3.10)
где l 0 – расчетная высота (длина) элемента;
δ ст–толщина стены.
 .
.
Гибкость сжатой части прямоугольного сечения λ с определяется по формуле:
λ c=  , (3.11)
, (3.11)
где l 0 – расчетная высота (длина) элемента, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, определяемая по формуле:
hc= δ ст -2e, (3.12)
где δ ст – толщина стены, м;
е – эксцентриситет, м.
 =δ ст–2е=0, 51 – 2·0, 0125=0, 485 (м).
=δ ст–2е=0, 51 – 2·0, 0125=0, 485 (м).
 .
.
По интерполяции по таблице 18 [7] находим коэффициенты φ и φ с:
φ =0, 98+(1–0, 98)  0, 9988
0, 9988
φ с=0, 95+(0, 98–0, 95)  0, 955
0, 955

Площадь сечения элемента находится по формуле:
Ас=bпрhс, (3.13)
гдеbпр– ширина простенка, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, м.
Ас=1, 81·0, 485=0, 877 (м2)
Коэффициент ω для прямоугольного сечения вычисляют по формуле:
 (3.14)
(3.14)
где е – эксцентриситет, м;
δ ст – толщина стены, м.
ω = 1 + 0, 0125 / 0, 51 =1, 024
1, 024  – условие выполняется.
– условие выполняется.
Проверяем по формуле 2.1:
N =1300< mgφ RAс ω = 1·0, 9769·2000·0, 877·1, 024=1754, 6 (кН)
Условие выполняется.
kз=1754, 6/1300=1, 35
Проверяю несущую способность простенка на 4-oм этаже
Для упрощения расчета разрешено рассматривать стену в пределах одного этажа как шарнирно опертую балку на двух опорах с расчетной длиной l0равной высоте этажа Н (см. рисунок 3.10)
Рисунок 3.10 – К расчету простенка
Величина изгибающего момента от этажа на уровне низа перекрытия 4-го этажа.
P=qперАгр=6, 036∙ 12, 04=72, 67 кН,
Мэ=Р(t/2-1/3c)=72, 67(0, 51/2-1/3∙ 0, 12)=15.62кНм
А момент на уровне низа перемычки (в расчетном сечении)
М=Мэ(Н-h1)/H=15.62(3-0.32)/3=13.9кНм,
МW=Wm∙ 0.32=2.22∙ 0.62=1.3764кНм,
Мп=М + МW=13.9+1.3764=15, 27кНм
Наиболее опасным местом в простенке, которое и необходимо рассчитывать, является сечение, расположенное по низу перемычки, так как в этом сечении кроме продольной силы действует изгибающий момент М, который определяется от воздействия реакций перекрытия и ветровой нагрузки (рисунок3.11), расположенного непосредственно над рассчитываемым сечением 1-1.
Рисунок 3.11 – Нагрузка от перекрытия на стену
Из рисунка 3.11 видно, что давление от перекрытия на стену принимается действующим неравномерно: по внутренней грани стены максимальным и равным нулю у конца плиты перекрытия (в сечении получается треугольник). При таком распределении давления равнодействующая напряжений Р прикладывается в центре тяжести треугольника на расстоянии (t/2-1/3c) от центра тяжести стены.
В целом на расчетное сечение действуют продольная сила N и изгибающий момент Мп или, что равнозначно, продольная сила прикладывается с эксцентриситетом е0=М/N3=15, 27/1162=0.0131м. (3.8)
Несущая способность внецентренно сжатых элементов без поперечного армирования проверяется по формуле
N≤ mgφ RAс ω,
Расчетное сопротивление кладки из кирпича R находится по таблице 2 [7]. Для кирпича марки 125 и раствора марки 100: R=2.0 МПа.
При h > 30см по [7] коэффициент mg =1.
Коэффициент продольного изгиба φ находится по формуле:
 , (3.9)
, (3.9)
где φ – коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый для расчетной высоты элемента l0 , по таблице 18 [7];
φ с – коэффициент продольного изгиба для сжатой части сечения, определяемый для фактической высоты элемента Н, по таблице 18 [7].
Гибкость элемента λ определяем по формуле:
 , (3.10)
, (3.10)
где l 0 – расчетная высота (длина) элемента;
δ ст–толщина стены.
 .
.
Гибкость сжатой части прямоугольного сечения λ с определяется по формуле:
λ c=  , (3.11)
, (3.11)
где l 0 – расчетная высота (длина) элемента, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, определяемая по формуле:
hc= δ ст -2e, (3.12)
где δ ст – толщина стены, м;
е – эксцентриситет, м.
 =δ ст–2е=0, 51 – 2·0, 0131=0, 484 (м).
=δ ст–2е=0, 51 – 2·0, 0131=0, 484 (м).
 .
.
По интерполяции по таблице 18 [7] находим коэффициенты φ и φ с:
φ =0, 98+(1–0, 98)  0, 9988
0, 9988
φ с=0, 95+(0, 98–0, 95)  0, 9522
0, 9522

Площадь сечения элемента находится по формуле:
Ас=bпрhс, (3.13)
гдеbпр– ширина простенка, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, м.
Ас=1, 81·0, 484=0, 876 (м2)
Коэффициент ω для прямоугольного сечения вычисляют по формуле:
 (3.14)
(3.14)
где е – эксцентриситет, м;
δ ст – толщина стены, м.
ω = 1 + 0, 0131 / 0, 51 =1, 025
1, 02  – условие выполняется.
– условие выполняется.
Проверяем по формуле 2.1:
N =1162< mgφ RAс ω = 1·0, 975·2000·0, 876·1, 025=1750 (кН)
Условие выполняется.
kз=1750/1162=1, 5
Проверяю несущую способность простенка на 5-oм этаже
Для упрощения расчета разрешено рассматривать стену в пределах одного этажа как шарнирно опертую балку на двух опорах с расчетной длиной l0равной высоте этажа Н (см. рисунок 3.12)
Рисунок 3.12 – К расчету простенка
Величина изгибающего момента от этажа на уровне низа перекрытия 5-го этажа.
P=qперАгр=6, 036∙ 12, 04=72, 67 кН,
Мэ=Р(t/2-1/3c)=72, 67(0, 51/2-1/3∙ 0, 12)=15.62кНм
А момент на уровне низа перемычки (в расчетном сечении)
М=Мэ(Н-h1)/H=15.62(3-0.32)/3=13.9кНм,
МW=Wm∙ 0.32=2.45∙ 0.62=1.52кНм,
Мп=М + МW=13.9+1.52=15, 42кНм
Наиболее опасным местом в простенке, которое и необходимо рассчитывать, является сечение, расположенное по низу перемычки, так как в этом сечении кроме продольной силы действует изгибающий момент М, который определяется от воздействия реакций перекрытия и ветровой нагрузки (рисунок3.13), расположенного непосредственно над рассчитываемым сечением 1-1.
Рисунок 3.13 – Нагрузка от перекрытия на стену
Из рисунка 3, 13 видно, что давление от перекрытия на стену принимается действующим неравномерно: по внутренней грани стены максимальным и равным нулю у конца плиты перекрытия (в сечении получается треугольник). При таком распределении давления равнодействующая напряжений Р прикладывается в центре тяжести треугольника на расстоянии (t/2-1/3c) от центра тяжести стены.
В целом на расчетное сечение действуют продольная сила N и изгибающий момент Мп или, что равнозначно, продольная сила прикладывается с эксцентриситетом е0=М/N3=15, 42/1024=0.015м. (3.8)
Несущая способность внецентренно сжатых элементов без поперечного армирования проверяется по формуле
N≤ mgφ RAс ω,
Расчетное сопротивление кладки из кирпича R находится по таблице 2 [7]. Для кирпича марки 125 и раствора марки 100: R=2.0 МПа.
При h > 30см по [7] коэффициент mg =1.
Коэффициент продольного изгиба φ находится по формуле:
 , (3.9)
, (3.9)
где φ – коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый для расчетной высоты элемента l0 , по таблице 18 [7];
φ с – коэффициент продольного изгиба для сжатой части сечения, определяемый для фактической высоты элемента Н, по таблице 18 [7].
Гибкость элемента λ определяем по формуле:
 , (3.10)
, (3.10)
где l 0 – расчетная высота (длина) элемента;
δ ст–толщина стены.
 .
.
Гибкость сжатой части прямоугольного сечения λ с определяется по формуле:
λ c=  , (3.11)
, (3.11)
где l 0 – расчетная высота (длина) элемента, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, определяемая по формуле:
hc= δ ст -2e, (3.12)
где δ ст – толщина стены, м;
е – эксцентриситет, м.
 =δ ст–2е=0, 51 – 2·0, 015=0, 48 (м).
=δ ст–2е=0, 51 – 2·0, 015=0, 48 (м).
 .
.
По интерполяции по таблице 18 [7] находим коэффициенты φ и φ с:
φ =0, 98+(1–0, 98)  0, 9988
0, 9988
φ с=0, 95+(0, 98–0, 95)  0, 953
0, 953

Площадь сечения элемента находится по формуле:
Ас=bпрhс, (2.13)
гдеbпр– ширина простенка, м;
hc – высота сжатой части поперечного сечения в плоскости действия изгибающего момента, м.
Ас=1, 81·0, 48=0, 8688 (м2)
Коэффициент ω для прямоугольного сечения вычисляют по формуле:
 (2.14)
(2.14)
где е – эксцентриситет, м;
δ ст – толщина стены, м.
ω = 1 + 0, 015 / 0, 51 =1, 03
1, 03  – условие выполняется.
– условие выполняется.
Проверяем по формуле 2.1:
N =1024< mgφ RAс ω = 1·0, 976·2000·0, 8688·1, 03=1746 (кН)
Условие выполняется.
kз=1746/1024=1, 7
| Этаж | Kз |
| 1, 086 | |
| 1, 2 | |
| 1, 35 | |
| 1, 5 | |
| 1, 7 |
Вывод: Наиболее нагруженный простенок находится на первом этаже.
|