
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Б) в прямоугольной диметрии
|
|
Окружности в аксонометрии изображаются в виде эллипсов. Каждый эллипс характеризуется большой и малой осью. Для прямоугольной изометрии большая ось равна 1, 22d, малая ось – 0, 71d. (рис. 31). Для прямоугольной диметрии большая ось эллипса равна 1, 06 d проецируемой окружности, малые оси 0, 35d и 0, 95d соответственно (рис. 33). На практике принято эллипсы заменять овалами, что значительно упрощает построения (рис. 32).


|
Рис. 31. Положение эллипсов в прямоугольной изометрии
2.3.1 Построение эллипса в прямоугольной изометрии
Построение овала, приближенно замещающего изометрическую проекцию окружности, рассмотрим на примере рис. 32.
1. Определяем размеры большой и малой оси эллипса. АВ = 1, 22d. CD = 0, 71d.
2. Через точку О проводим две взаимно перпендикулярные прямые, на которых отложим соответственно размеры большой и малой осей.

Рис. 32. Построение эллипса
3. Из точки О радиусами равными ОА и ОС строим окружности и определяем точки О1; О2; О3; О4 которые являются центрами сопряжения дуг овала.
4. Затем описываем дуги из центров О1 и О2 радиусом R1 = O1C и R2 =O2D, а из центров О3 и О4 – дуги радиусом R2 = O3A и R2 =O4B.
2.3.2 Построение эллипсов в прямоугольной диметрии в плоскости П1 и П3
Построение эллипсов приближенно замещающего проекцию окружности, в прямоугольной диметрии, лежащей в плоскости П1 и П3 рассмотрим на рис. 33.
1. Определяем размеры большой и малой оси: АВ = 1, 06d, CD = 0, 35d.
2. Через точку О проводим две взаимно перпендикулярные прямые размером большой и малой оси. (рис. 33 а)
3. Точки О1 и О2 – являются центрами больших дуг овала, точки О3 и О4, центрами малых дуг.
4. Из точки О1 и О2 радиусами равными R1 =O1C и O2D проводим дуги окружностей, из точки О3 и О4 - R2 = O3A и O4B – замыкающие дуги.

| 
|
Рис. 33. а, б – Построение эллипсов в прямоугольной диметрии, в плоскости П1 и П3
2.3.3 Построение эллипса в прямоугольной диметрии в плоскости П2
1. Определяем размеры большой и малой осей АВ = 1, 06d, CD = 0, 95d.
2. Через точку О проводим аксонометрические оси ox, oy, oz.
3. В точке О перпендикулярно оси oy проводим прямую, и отложим на ней величину равную АВ, малая ось эллипса совпадает с oy.
4. На осях ox и oz от точки О отложим отрезки равные величине радиуса окружности и получим точки M, N, E, F, которые являются точками сопряжения дуг овала (OM=ON=OE=OF=R=d/2).
5. Из точек M и N проводим прямые, перпендикулярные оси oz, которые пересекаясь с осью oy и АВ дают точки О1, О2, О3, О4 – центры дуг овала (рис. 34 а).
6. Из точек О2 и О4 – радиусом R1=O2M описываем дуги, и из точек О1 и О3 – радиусом R2=O3N (рис 34 б).
Направление осей эллипсов зависит от положения проецируемой окружности: большая ось – всегда перпендикулярна той аксонометрической оси, которой нет в плоскости заданной окружности, а малая ось совпадает с направлением этой оси. (рис. 35)
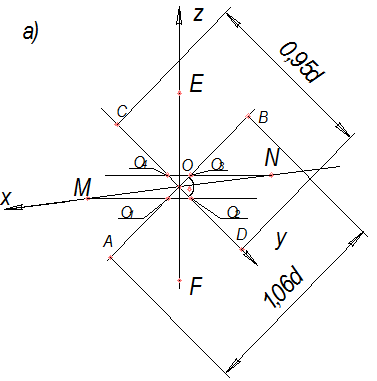

Рис. 34. а, б – Построение эллипса в прямоугольной диметрии, в плоскости П2
    
|

Рис. 35. Положение эллипсов в прямоугольной диметрии
 y y
y y