
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вывод формулы Шеннона
|
|
К. Шеннон, используя подход Р. Хартли, обратил внимание на то, что при передаче словесных сообщений частота (вероятность) использования различных букв алфавита не одинакова: некоторые буквы используются очень часто, другие - редко.
Рассмотрим алфавит Am состоящий из m символов. Обозначим через pi вероятность (частоту) появления i-ого символа в любой позиции передаваемого сообщения, состоящего из n символов. Один i – ый символ
алфавита несёт количество информации равное -Log2(pi). Перед логарифмом стоит «минус» потому, что количество информации величина неотрицательная, а Log2(x) < 0 при 0< x< 1.
На месте каждого символа в сообщении может стоять любой символ алфавита Am; количество информации, приходящееся на один символ сообщения, равно среднему значению информации по всем символам алфавита Am:
 (3.1) i =1
(3.1) i =1
Общее количество информации, содержащееся в сообщении из n символов
равно:
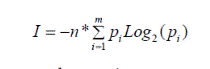 (3.2)
(3.2)
Если все символы алфавита Am появляются с равной вероятностью,
то все pi = p. Так как Σ рi = 1, то p = 1/m.).
 =
=
Вывод: формула Шеннона (3.2) в случае, когда все символы алфавита равновероятны, переходит в формулу Хартли (2.2).
В общем случае количество энтропии H произвольной системы X (случайной величины), которая может находиться в m различных состояниях x1, x2, … xm c вероятностями p1, p2, … pm, вычисленное по формуле Шеннона, равно
 (3.3)
(3.3)
Напомним, что p1+ p2+ … +pm = 1. Если все pi одинаковы, то все состояния системы X равновероятны; в этом случае pi = 1/m, и формула
(3.3) переходит в формулу Хартли (2.5): H(X) = Log2(m).
Замечание. Количество энтропии системы (случайной величины) Х не зависит от того, в каких конкретно состояниях x1, x2, … xm может находиться система, но зависит от числа m этих состояний и от
вероятностей p1, p2, … pm, с которыми система может находиться в этих состояниях. Это означает, что две системы, у которых число состояний одинаково, а вероятности этих состояний p1, p2, … pm равны (с точностью до порядка перечисления), имеют равные энтропии.