
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Итерационные циклы
|
|
Для вычислений с заранее неизвестным количеством повторений итераций обычно используются операторы while и do while, однако C++ позволяет использовать для этих целей и оператор for.
Циклический процесс, выполняющийся до достижения некоторого условия, называется итерационным. Учитывая неизвестность конечного числа шагов итерационного алгоритма, необходимо предусмотреть вариант зацикливания и сформулировать корректное условие для выхода из цикла. В самом простом случае, а также на этапе отладки алгоритма, достаточно поставить лимит числа шагов с выдачей сообщения в случае его исчерпания.
В итерационных алгоритмах заданная погрешность используется для проверки модуля разности найденного приближенного и точного значений. В случае, когда точное значение неизвестно, допустимо оценивать разность между соседними итерациями.
Значащими цифрами числа называются все цифры в его десятичной записи, кроме крайних левых и крайних правых нулей.
При решении задач, как правило, нет необходимости хранить промежуточные итерации – достаточно получения окончательного результата и (в итерационных алгоритмах) числа шагов, проделанных для достижения условия – для оценки скорости сходимости алгоритма.
Часто в задачах для вычисления очередного слагаемого удобно рекуррентно использовать предыдущее слагаемое, а не организовывать дополнительный (внутренний) цикл.
Рассмотрим пример использования итерационных циклов. Возьмем ту же задачу, что и для вложенных циклов, но несколько модифицируем ее.
Составить программу вычисления значения функции
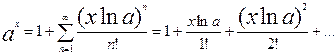
с погрешностью e = 10-3 и напечатать для контроля значения функции, определяемые выражениями в правой и левой частях равенства.
Сколько итераций надо выполнить, чтобы для заданной погрешности e было справедливо соотношение  ?
?
Решение. Вычисление факториала можно организовать рекуррентно, т.е. умножая каждый раз некоторую переменную на значение счетчика n. Вычисление рекуррентных значений можно осуществить на основе следующей формулы:

Поэтому нет необходимости вычислять факториал каждый раз заново, достаточно домножить предыдущее значение на значение переменной n.
Аналогичным образом можно вычислить и операцию возведения в степень (значение (x*log(a))n в примере). Для этого используется формула:

Здесь тоже нет необходимости вычислять степень числа каждый раз заново, достаточно домножить предыдущее значение на x.
#include " stdafx.h"
#include < iostream>
#include < iomanip>
#include < math.h>
using namespace std;
void main ()
{
const float eps = 0.001f;
float a, x, xn = 1, y, y0;
unsigned int n = 1, nf = 1;
cout < < " Input a, x: " < < endl;
cin > > a > > x;
y = 1;
Do
{
nf *= n;
xn *= x * log ( a );
y0 = y;
y += xn / nf;
n ++;
}
while ( abs ( y - y0 ) > eps );
y0 = pow ( a, x );
cout < < " Result of iterative calculation: " < < setw ( 9 ) < < \
setprecision ( 5 ) < < y < < endl;
cout < < " Result of direct calculation: " < < setw ( 9 ) < < \
setprecision ( 5 ) < < y0 < < endl;
cout < < " Number of iterations: " < < setw ( 5 ) < < n < < endl;
}
Рассмотрим переменные и порядок вычисления данного примера.
Назначение переменных a и x понятно из формулы.
eps - заданная погрешность вычисления.
nf – переменная для хранения факториала.
xn – переменная для хранения (x*log(a))n.
y – переменная для хранения текущего значения функции.
y0 – переменная для хранения значения функции на предыдущем шаге.
В начале мы вводим значения a и x с клавиатуры.
Объявляем необходимые переменные. При этом задаем начальные значения для счетчика итераций n и хранения значения nf и xn.
Затем присваиваем начальное значение для текущего значения функции y (первое слагаемое ряда равное 1).
Далее организуем цикл с постусловием. В начале цикла обновим значение факториала для n-ого шага nf. и значение (x*log(a))n - xn. Затем сохраняем значение y в переменную y0. Вычислим новое значение функции путем добавления нового слагаемого из формулы и увеличим значение счетчика итераций.
Признаком окончания цикла будет служить условие из задания, т.е. модуль разности между текущим значением функции и значением на предыдущем шаге должны быть меньше заданной погрешности вычисления.
Далее, по завершению цикла, вычисляем значение функции через стандартные функции языка C++ и выводим полученные значения на экран, отформатировав вывод при помощи манипуляторов потокового ввода-вывода. Также покажем количество итераций, потребовавшихся для достижения требуемой точности.
Замечание. Поскольку значение факториала растет чрезвычайно быстро (12! = 479 001 600, а 13! = 6 227 020 800), значения свыше 12! уже не помещаются в переменную типа int. Поэтому результаты с количеством итераций больше 12 будут содержать значительные погрешности. Это происходит из-за явления оборачивания, суть которого можно кратко выразить такими соотношениями:
0xFFFF + 0x0001 = 0x0000
0x0000 – 0x0001 = 0xFFFF
Т.е если последовательно увеличивать содержимое какой-либо целочисленной беззнаковой переменной, то, достигнув верхнего возможного предела, число превысит эту границу, станет равным нулю и продолжит нарастать в области малых положительных чисел (1, 2, 3, и т.д.). Точно так же, если последовательно уменьшать некоторое число, то оно, достигнув нуля, перейдет в область больших положительных.
Это же касается и чисел со знаком: достигнув верхнего положительного предела, число превысит эту границу, станет равным минимальному отрицательному числу, а если последовательно уменьшать некоторое отрицательное число, то оно, достигнув минимального значения, оно перейдет в область больших положительных.
Увидеть явление оборачивания можно на следующем примере.
#include " stdafx.h"
#include < iostream>
#include < iomanip>
#include < math.h>
using namespace std;
void main ()
{
unsigned int n = 0;
signed int m = 2147483647;
cout < < n < < endl;
n --;
cout < < n < < endl;
n ++;
cout < < n < < endl;
cout < < endl;
cout < < m < < endl;
m ++;
cout < < m < < endl;
m --;
cout < < m < < endl;
}
Результаты работы:
-2147483648
Контрольные вопросы
1. Каково предназначение итерационных циклов? Каким образом их можно реализовать?
2. Каково предназначение арифметических циклов? Каким образом их можно реализовать?
3. Каково предназначение вложенных циклов? Каким образом их можно реализовать?
4. Перечислите виды операторов цикла и опишите их работу.
5. Опишите возможности ввода-вывода данных с помощью библиотеки потокового ввода вывода iostream.h.
6. Опишите известные вам манипуляторы ввода-вывода.
7. Как осуществляется ввод при помощи стандартной библиотеки stdio.h?
8. Какие модификаторы и спецификаторы поддерживает функция printf.
9. Что такое явление оборачивания, и каковы его возможные последствия.