Последовательное отсечение многоугольника — алгоритм Сазерленда — Ходжмена

Основная идея алгоритма Сазерленда — Ходжмена состоит в том, что отсечь многоугольник относительно одной прямой или плоскости очень легко. В этом алгоритме исходный и каждый из промежуточных многоугольников отсекается последовательно относительно одной прямой. Порядок отсечения многоугольника разными сторонами окна непринципиален.

Результатом работы алгоритма является список вершин многоугольника, у которого все вершины лежат по видимую сторону от очередной отсекающей плоскости. Поскольку каждая сторона многоугольника отсекается независимо от других, то достаточно рассмотреть только возможные ситуации расположения одного отрезка относительно одной отсекающей плоскости. Будем рассматривать каждую точку Р из списка вершин многоугольника, за исключением первой, как конечную точку ребра, начальной точкой S которого является вершина, предшествующая Р в этом списке. Тогда возможны только четыре ситуации взаимного расположения ребра и отсекающей плоскости (ОП) (рис. 17).

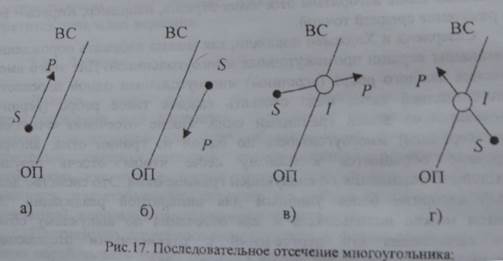
ВС -- видимая сторона

Результатом каждого сопоставления ребра многоугольника с отсекающей плоскостью будет занесение в список вершин результирующего усеченного многоугольника нуля, одной или двух вершин. Если рассматриваемое ребро полностью видимо, то результатом будет вершина Р. Заносить в результат начальную вершину S в этом случае нс надо, так как если вершины рассматриваются поочередно, то S уже была конечной точкой предыдущего ребра и поэтому уже попала в результат (рис. 17, а). Если же ребро полностью невидимо, то результат не изменяется (рис. 17, 6).

Если ребро многоугольника видимо неполностью, то оно может или входить или выходить из области видимости отсекающей плоскости. Если ребро выходит из области видимости, то надо определить и занести в результат точку пересечения ребра и отсекающей плоскости (рис. 17, в). Если же ребро входит в область видимости (рис. 17, г), то следует поступить точно так же. Поскольку в последнем случае конечная вершина Р ребра видима, то она также должна попасть в результат.

Для первой вершины многоугольника необходимо определить только факт её видимости. Если вершина видима, то она попадает в результат и становится начальной точкой S. Если же вершина невидима, она тоже становится начальной точкой, но в результат не попадает.

Определение видимости точки эквивалентно определению той стороны границы отсекающей плоскости, по которую лежит эта точка. Можно воспользоваться ранее рассмотренным алгоритмом, который сводится к. определению знака скалярного произведения вектора нормали на вектор, начинающийся в произвольной точке на прямой или плоскости и заканчивающийся в пробной точке. Ребро многоугольника будет полностью видимым, если оба его конца видимы, и полностью невидимым, если оба они не видны. Если же один конец ребра видим, а другой невидим, то ребро пересекается с отсекающей плоскостью и нужно вычислять точку пересечения. Для этого можно использовать любые изложенные выше алгоритмы отсечения отрезка, например, Кируса - Бека или разбиение средней точкой.

Сазерленд и Ходжмен показали, как можно избежать порождения и запоминания вершин промежуточных многоугольников. Для этого вместо отсечения каждого ребра (вершины) многоугольника одной плоскостью, ограничивающей окно, надо отсекать каждое такое ребро (вершину) последовательно всеми границами окна. После отсечения очередного ребра (вершины) многоугольника по одной из границ окна, алгоритм рекурсивно обращается к самому себе, чтобы отсечь результат предыдущего обращения по следующей границе окна. Это свойство делает данный алгоритм более удобным для аппаратной реализации. Этот алгоритм можно использовать и для отсечения по выпуклому объёму путём вычисления его пересечений с трёхмерными отсекающими плоскостями при помощи алгоритма Кируса - Бека.