
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение разверток поверхностей тел
|
|
Для изготовления кожухов машин, ограждений станков, вентиляционных устройств, трубопроводов необходимо из листового материала вырезать их развертки.
Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью чертежа всех граней многогранника в последовательности их расположения на многограннике.
Чтобы построить развертку поверхности многогранника, нужно определить натуральную величину граней и вычертить на плоскости последовательно все грани. Истинные размеры ребер граней, если они спроецированы не в натуральную величину, находят способами вращения или перемены плоскостей проекций (проецированием на дополнительную плоскость), приведенными в предыдущем параграфе.
Рассмотрим построение разверток поверхности некоторых простейших тел.
Развертка поверхности прямой призмы представляет собой плоскую фигуру, составленную из боковых граней - прямоугольников и двух равных между собой многоугольников оснований. Для примера взята правильная прямая шестиугольная призма (рис. 176, а). Все боковые грани призмы - прямоугольники, равные между собой по ширине а и высоте Н; основания призмы - правильные шестиугольники со стороной, равной а. Так как истинные размеры граней нам известны, нетрудно выполнить построение развертки. Для этого на горизонтальной прямой последовательно откладывают шесть отрезков, равных стороне основания шестиугольника, т. е. 6а. Из полученных точек восставляют перпендикуляры, равные высоте призмы Н, и через конечные точки перпендикуляров проводят вторую горизонтальную прямую. Полученный прямоугольник (Н х 6а) является разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуры оснований - два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сгиба - штрихпунктирной с двумя точками.
Подобным образом можно построить развертки прямых призм с любой фигурой в основании.
Развертка поверхности правильной пирамиды представляет собой плоскую фигуру, составленную из боковых граней - равнобедренных или равносторонних треугольников и правильного многоугольника основания. Для примера взята правильная четырехугольная пирамида (рис. 176, б). Решение задачи осложняется тем, что неизвестна величина боковых граней пирамиды, так как ребра граней не параллельны ни одной из плоскостей проекций. Поэтому построение начинают с определения истинной величины наклонного ребра SA. Определив способом вращения (см. рис. 173, в) истинную длину наклонного ребра SA, равную s'a`1 (рис. 176, б), из произвольной точки О, как из центра, проводят дугу радиусом s'a`1. На дуге откладывают четыре отрезка, равные стороне основания пирамиды, которое спроецировано на чертеже в истинную величину. Найденные точки соединяют прямыми с точкой О. Получив развертку боковой поверхности, к основанию одного из треугольников пристраивают квадрат, равный основанию пирамиды.
Развертка поверхности прямого кругового конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. 176, в). Построение выполняют следующим образом. Проводят осевую линию и из точки, взятой на ней, как из центра, радиусом Rh равным образующей конуса sfd, очерчивают дугу окружности. В данном примере образующая, подсчитанная по теореме Пифагора, равна приблизительно
38 мм (L = √ l52 + 352 = √ l450 ≈ % 38 мм). Затем подсчитывают угол сектора по формуле

где R - радиус окружности основания конуса; L - длина образующей боковой поверхности конуса.
В данном примере α = 360°⋅ 15/38 ≈ 142, 2°.
Этот угол строят симметрично относительно осевой линии с вершиной в точке s. К полученному сектору пристраивают круг с центром на осевой линии и диаметром, равным диаметру основания конуса.
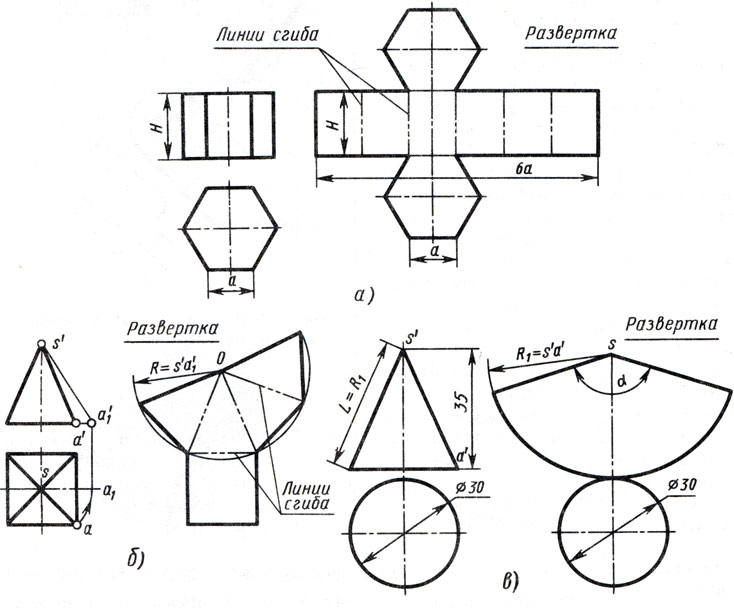
Рис. 176. Чертеж разверток поверхностей геометрических тел