
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель эллипсоида
|
|
Рисунок 3.5 – Преобразование отражения относительно плоскости XOY
3.2.5 Преобразования сдвига
На рис. 3.6 приведен пример сдвига вдоль оси ОХ.
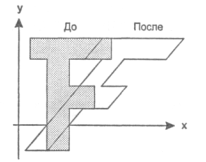
Рисунок 3.6 – Двумерный сдвиг относительно оси OХ
В этом случае координата у каждой точки остается неизменной, а каждая координата х перемещается на величину, которая линейно возрастает с ростом у. Трехмерный сдвиг описывается следующей матрицей:
 (3.9)
(3.9)
Здесь Shx, Shy, Shz – параметры сдвига вдоль осей OX, OY, OZ соответственно.
3.3 Проецирование. Виды проецирования
Несоответствие между пространственными объектами и плоскими изображениями устраняется путем введения проекций, которые отображают объекты на картинной двумерной проекционной плоскости.
Проецированием называется процесс получения изображения объекта на проецирующей (картинной) плоскости путем помещения всех точек объекта на эту плоскость. Для получения нормального изображения необходимо, чтобы над каждой точкой объекта выполнялось одинаковое преобразование. В общем случае различают два типа проецирования: параллельное и центральное (см. рис. 3.7). Каждый из этих двух типов имеет свои подтипы.

Рисунок 3.7 – Параллельное (слева) и центральное проецирование
3.3.1 Параллельное ортографическое проецирование
Параллельное проецирование на картинную плоскость проводится пучком параллельных прямых, проходящих под определённым углом к картинной плоскости. В случае ортографического проецирования в качестве картинной плоскости выступает одна из координатных плоскостей, а пучок параллельных прямых перпендикулярен ей. Математически параллельное ортографическое проецирование выражается в обнулении координаты точки, соответствующей оси, перпендикулярной проецирующей плоскости. Матрица ортографического проецирования получается из единичной матрицы путем обнуления соответствующего диагонального элемента. Так, матрицы проецирования на плоскости ХOY, YOZ, ХOZ будут следующими:
 (3.10)
(3.10)
 (3.11)
(3.11)
 (3.12)
(3.12)

Рисунок 3.8 – Параллельное проецирование
3.3.2 Параллельное косоугольное проецирование
Косоугольная проекция формируется параллельными проекторами с центром, лежащим в бесконечности, и расположенными под косым углом к плоскости проекции. Общая схема проекции изображена на рисунке 3.9.

Рисунок 3.9 – Параллельное косоугольное проецирование
Особый интерес представляет косоугольные проекции кавалье (свободная). Проекция кавалье получается, когда угол между проекторами и плоскостью проекции составляет 45°. В этой проекции коэффициенты искажения для всех трех главных направлений одинаковы. Результат этой проекции выглядит неестественно утолщенным. Матрица проекции кабине на плоскость XOY имеет следующий вид:
 (3.13)
(3.13)
Здесь ƒ — длина спроецированного единичного вектора на оси z, т.е. коэффициент искажения, а α — угол между горизонталью и спроецированной осью z.
На рисунке 3.10 изображена свободная проекция куба.


Рисунок 3.10 – свободная проекция куба
3.3.2 Изометрическое проецирование
Изометрия является разновидностью аксонометрического проецирования. Изометрией называется такое параллельное проецирование, при котором вектор нормали картинной плоскости (плоскости проецирования) попарно образуют одинаковые углы с ортами координатных осей (рисунок 3.11).

Рисунок 3.11 – Пример изометрического проецирования
Плоскость проецирования пересекает координатные оси в точках dx, dy, dz и задается нормальным вектором N (перпендикулярен плоскости проецирования). Путем параллельного проецирования точка А проецируется в точку А' на плоскость (dx, dy, dz).
По определению изометрического проецирования, вектор N должен образовывать попарно равные углы с ортами координатных осей. Это возможно лишь в случае, когда угол наклона равен 45°. Координаты ортонормированного вектора N(Nx, Ny, Nz) вычисляются следующим образом:
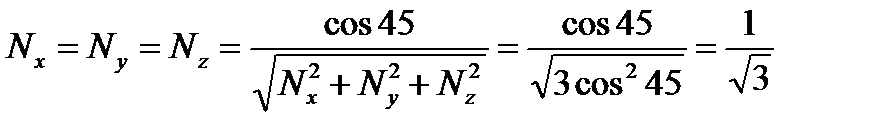 . (3.2)
. (3.2)
3.3.3 Диметрическая проекция
Диметрическая проекция - это аксонометрическая проекция, у которой коэффициенты искажения по двум осям имеют равные значения, а искажение по третьей оси может принимать иное значение.
В целях упрощения построений, как и в изометрических проекциях, приведенный коэффициент искажения по осям x и z принимают равным 1; по оси y коэффициент искажения равен 0, 5. По осям x и z или параллельно им все размеры откладывают в натуральную величину, по оси y размеры уменьшают вдвое. Расположение осей Ox и Oy в диметрической проекции показано на рис. 3.12.

Рисунок 3.12 - Расположение осей Ox и Oy в диметрической проекции показано
Коэффициент искажения по оси y равен 0.47, а по осям x и z - 0.94.
Диметрическую проекцию, как правило, без искажения по осям x и z и с коэффициентом искажения 0.5 по оси y.
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы.
Если димметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1, 06 диаметра окружности, а малая ось эллипса 1 - 0.95, эллипсов 2 и 3 - 0.35 диаметра окружности.
Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 - 0.9, эллипсов 2 и 3 - 0, 33 диаметра окружности.
3.4 Модели представления объектов
Существует два основных способа представления трехмерных объектов на экране. Первая из моделей - каркасная (проволочная) отображает основные линии, составляющие объект. Проволочная модель реализуется достаточно просто: она задается множеством точек (вершин) объекта и множеством ребер. Каждое ребро представляет собой объединение двух вершин, содержащихся в множестве. Таким образом, при отрисовке на экране виден каркас объекта. Второй вид модели применяется гораздо чаще, она является более практичной, суть ее заключается в задании треугольных граней объекта. Каждая грань определяется как треугольник. Такая модель называется полигональной. Полигональная модель удобна тем, что позволяет применить множество алгоритмов закраски, сортировки, отсечения невидимых граней.
3.5 Управление камерой
3.5.1. Мировая и локальная системы координат
Мировая система координат – общая система координат, заданная началом координат и тремя ортонормированными векторами.
Локальная система координат (система координат связанная с самим объектом) вводит свою точку отсчета и направление координатных осей. В мировой системе координат можно описать бесконечное множество локальных систем координат (например, для каждого объекта).
3.5.2 Модель камеры
Совокупность объектов мировой системы координат определяют сцену. К объектам сцены относятся как трехмерные объекты, так и камеры, задающие видовые операции. Камера управляет проецированием. Каждая камера задается следующими параметрами:
- положение в мировой системе координат;
- направление камеры (главная оптическая ось);
- угол зрения камеры;
- угол поворота относительно главной оптической оси.
Камера показана на рисунке 3.10.
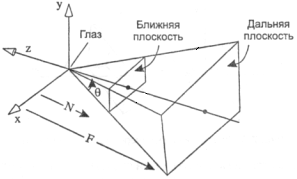
Рисунок 3.10 – Камера
Величина Ө - угол зрения камеры, N — это расстояние от глаза до ближней плоскости, a F — расстояние от глаза до дальней плоскости. N и F должны быть положительными.
3.5.3 Типичные преобразования камер
Камера представляет собой обычный объект, заданный в локальной системе координат и определяет перспективные или параллельные проекции. Точка проецирования называется фокусом. В локальной системе координат эта точка находится на главной оптической оси.
Типичные операции управления камерой:
а) зуммирование – изменение угла зрения или расстояния до центральной точки. При зуммировании камера остается на месте. Матрица зуммирования может быть получена путем умножения матриц двух последовательных преобразований: перспективного преобразования и проецирования на плоскость OXZ;
б) панорамирование – камера поворачивается влево вправо. Матрица панорамирования совпадает с матрицей поворота вокруг оси OZ;
в) вертикальное панорамирование – поворот вверх-вниз. Матрица вертикального панорамирования совпадает с матрицей поворота вокруг оси OX;
г) вращение камеры вокруг главной оптической оси. Матрица вращения вокруг главной оптической оси совпадает с матрицей поворота вокруг оси ординат OY’ локальной системы координат. Поворот аналогичен повороту вокруг оси ординат OZ;
д) перенос влево-вправо и вверх-вниз относительно главной оптической оси.
е) наезд и откат камеры – перемещение камеры вдоль главной оптической оси. В этом случае изменяется положение камеры в мировой системе координат;
3.6 Методы удаления невидимых граней
При использовании полигональной модели возникает проблема отрисовки невидимых граней. Проблема заключается в порядке вывода на экран граней объекта. Для решения данной задачи используется несколько подходов.
3.6.1 Алгоритм z-буфера
Одним из самых простых алгоритмов удаления невидимых граней и поверхностей является метод z-буфера (буфера глубины), где для каждого пикселя находится грань, ближайшая к нему вдоль направления проектирования.
Для вывода на картинную плоскость произвольной грани она переводится в растровое представление на картинной плоскости и затем для каждого пикселя этой грани находится его глубина. В случае если эта глубина меньше значения глубины, хранящегося в z-буфере, пиксель рисуется и его глубина заносится в z-буфер.
Грань рисуется последовательно строка за строкой; для нахождения значений используется линейная интерполяция.
Фактически метод z-буфера осуществляет поразрядную сортировку по x и y, а затем сортировку по z, требуя всего одного сравнения для каждого пикселя каждой грани.
Метод z-буфера работает исключительно в пространстве картинной плоскости и не требует никакой предварительной обработки данных. Порядок, в котором грани выводятся на экран, не играет никакой роли.
3.6.2 Алгоритм художника
Пусть имеется некий набор граней (т.е. объект), который требуется нарисовать. Отсортируем грани по удаленности от камеры и отрисуем все грани, начиная с самых удаленных. Довольно распространенная характеристика удаленности для грани ABC - это среднее значение z, mid_z = (A.z+B.z+C.z)/3. Таким образом, суть алгоритма достаточно проста. Однако существует несколько проблем – в некоторых случаях алгоритм вообще не может дать правильного результата, - в каком порядке грани не рисуй, получится неправильно.
3.7 Закраска граней
Основным преимуществом полигональных моделей является возможность закраски каждой из граней объекта в соответствии с её освещенностью. Интенсивность освещенности произвольной точки пространства вычисляется по формуле:
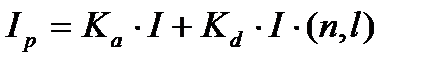 , (3.3)
, (3.3)
где Ip - интенсивность освещенности в точке,
Ка- коэффициент отражения;
Kd- коэффициент рассеивания;
I- интенсивность источника света;
n- единичная нормаль к грани, содержащей точку;
l- единичный вектор от точки к источнику света.
Каждый подход предусматривает определённый уровень реалистичности изображения. С повышением реалистичности изображения скорость алгоритма падает. Ниже будет рассмотрен один метод затенения объектов: плоское затенение.
Это простейший способ затенения. Для произвольной точки грани вычисляется интенсивность по формуле (3.3) и считается, что для всех точек грани интенсивность одинакова. В качестве точки для вычисления интенсивности не желательно брать граничные точки грани. Изображение носит явный полигональный характер.
4 ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ
4.1 Геометрическая модель куба
Куб задаётся единственным параметром w –длина ребра и состоит из восьми вершин: A11, A12, A13, A14 – вершины нижнего основания и A21, A22, A23, A24 – вершины верхнего основания. Пусть начало локальной системы координат куба совпадает с его геометрическим центром. Тогда координаты его вершин будут вычисляться следующим образом:
A11=(-w/2, -w/2, -w/2);
A12=(-w/2, -w/2, w/2);
A13=(w/2, -w/2, w/2);
A14=(w/2, -w/2, -w/2);
A21=(-w/2, w/2, -w/2);
A22=(-w/2, w/2, w/2);
A23=(w/2, w/2, w/2);
A24=(w/2, w/2, -w/2);
Геометрическая модель куба представлена на рисунке 4.1.
| X |
| Z |
| A11 |
| Y |
| A12 |
| A13 |
| A14 |
| A11 |
| A12 |
| A13 |
| A14 |
Рисунок 4.1 – Геометрическая модель куба
4.2 Геометрическая модель сферы
В графической базе данных сфера представляется тройкой вида (r, m, n), где r – радиус сферы, m – количество разбиений на вертикальной полуокружности при построении 0-го меридиана (тот на котором расположены точки на рисунке), n – количество разбиений на горизонтальной окружности при построении каждой из параллелей. Центр локальной системы координат связывается с геометрическим центром сферы. Изображение сферы приведено на рисунке 4.2.

Рисунок 4.2 - Геометрическая модель сферы
Для построения сферы необходимо проделать следующие шаги.
1. Построить точку с координатами (0, 0, r) в локальной системе координат сферы.
2. Построить 0-вой меридиан. Каждая i-я точка 0-го меридиана получается из предыдущей методом вращения вокруг оси Х. Угол поворота точки при построении 0-го меридиана определяется как π /m. Координата следующей точки определяется по формуле:
Pi=Pi-1*ПоворотOX(π /m). (4.1)
Параллели получаются вращением 0-го меридиана вокруг оси OZ на угол 2π /n. Каждый следующий меридиан получается из предыдущего по формуле:
Mi=Mi-1*ПоворотOZ(π /n). (4.2)
4.3 Геометрическая модель полусферы
Для построения геометрической модели полусферы, необходимо учесть 3 параметра: количество разбиений по ширине (m), количество разбиений по высоте (n) и радиус сферы (r). Пусть основание полусферы лежит в плоскости XOZ, а часть полусферы без основания – со стороны положительного направления оси OY.
Для аппроксимации полусферы, необходимо построить n ломаных, состоящих из m точек.
Первая точка первой ломаной имеет координаты a11(0, r, 0), координаты остальных m-1 точек будем находить по формуле:
Aij+1=Aij*ПоворотOZ(-180/(m-1)). (4.3)
Координаты точек i-ой ломаной будем вычислять по формуле:
Ai+1j=Aij*ПоворотOY(-180/(n-1)). (4.4)
Геометрическая модель полусферы приведена на рисунке 4.3.
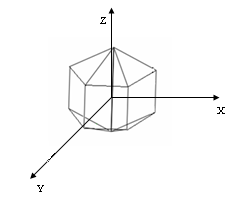
Рисунок 4.3 – Геометрическая модель полусферы
4.4 Геометрическая модель треугольной косоугольной призмы
Данный объект задаётся тремя параметрами: высота, радиус окружности, в которую вписано основание, смещение верхнего основания относительно нижнего вдоль оси OX. Обозначим эти параметры соответственно буквами h, r и s.
Пусть центр нижнего основания совпадает с началом локальной системы координат, а часть призмы без основания находится со стороны положительного направления оси OZ. Первая точка нижнего основания имеет координаты A11=(0, r, 0). Тогда координаты остальных точек нижнего снования будем находить по следующей формуле:
A1i+1= A1i*ПоворотOZ(360/3), (4.5)
а координаты точек нижнего основания – по формуле:
A2i+1= A2i*ПоворотOZ(360/3)*Перемещение(s, 0, h). (4.6)
Вид геометрической модели треугольной косоугольной призмы приведен на рисунке 4.4.
| x |
| z |
| y |
| A1i |
| A2i |
Рисунок 4.4 – Геометрическая модель треугольной косоугольной призмы
4.5 Геометрическая модель призмы с треугольным основанием
Данный объект задаётся двумя параметрами: высота и радиус окружности, в которую вписано основание. Обозначим эти параметры соответственно буквами h и r.
Пусть центр нижнего основания совпадает с началом локальной системы координат, а часть призмы без основания находится со стороны положительного направления оси OZ. Первая точка нижнего основания имеет координаты A11=(0, r, 0). Тогда координаты остальных точек нижнего снования будем находить по следующей формуле:
A1i+1= A1i*ПоворотOZ(360/3), (4.7)
а координаты точек верхнего основания – по формуле:
A2i+1= A2i*ПоворотOZ(360/3)*Перемещение(0, 0, h). (4.8)
Вид геометрической модели призмы с треугольным основанием приведен на рисунке 4.5.
| z |
| x |
| y |
| A1i |
| A2i |
Рисунок 4.5 – Геометрическая модель призмы с треугольным основанием
Модель эллипсоида
Эллипсоид в графической базе данных задается следующими параметрами:
- r – радиус эллипсоида;
- h – половина высоты эллипсоида;
- n – количество разбиений на вертикальной полуокружности,
- m – количество разбиений на горизонтальной полуокружности.
Рассмотрим построение геометрической модели эллипсоида с помощью меридиан и параллелей, центр локальной системы координат свяжем с геометрическим центром эллипсоида, оси которой направлены произвольно. Построение геометрической модели представлено на рисунке 4.6.
| z |
| β |
| α |
| x |
| y |
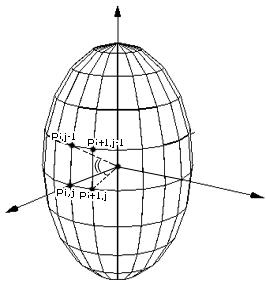
Рисунок 4.6 – Модель эллипсоида
Построение эллипсоида начинаем с построения точки с координатами Р00(0, 0, r). Затем строится нулевой меридиан (кривая разбивается на n точек) по формуле:
| (4.9) |
 ,
,
где 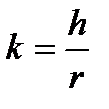 - коэффициент растяжения;
- коэффициент растяжения;
 - угол поворота.
- угол поворота.
Построенная ломаная, точки P0, 0…Pn, 0 - нулевой меридиан.
Построение параллелей производится путем вращения нулевого меридиана вокруг оси Z на угол α = 2π /m.
Следовательно, в графической базе данных модель эллипсоида можно задать с помощью формулы (4.10):
Эллипсоид(r, h, n, m) (4.10)
где r – радиус эллипсоида, h – высота половыны эллипсоида, n - количество меридиан, m - количество параллелей.
4.7 Геометрическая модель косоугольного конуса
Косоугольный конус задаётся четырьмя параметрами: высота, радиус основания, смещение вершины конуса относительно центра основания вдоль оси OX, количество разбиений основания. Обозначим эти параметры соответственно буквами h, r, s и n.
Пусть центр основания совпадает с началом локальной системы координат, а часть конуса без основания находится со стороны положительного направления оси OZ. Первая точка основания имеет координаты A1=(0, r, 0). Тогда координаты остальных точек снования будем находить по следующей формуле:
Ai+1= Ai*ПоворотOZ(360/n), (4.11)
а координаты вершины конуса будут равны (s, 0, h).
Вид геометрической модели косоугольного конуса приведен на рисунке 4.6.
| X |
| Z |
| Y |
| Ai |
Рисунок 4.6 – Вид геометрической модели косоугольного конуса
4.8 Геометрическая модель пирамиды с пятиугольным основанием
Пирамида с пятиугольным основанием задаётся двумя параметрами: высота и радиус окружности, в которую вписано основание. Обозначим эти параметры соответственно буквами h и r.
Пусть центр основания совпадает с началом локальной системы координат, а часть пирамиды без основания находится со стороны положительного направления оси OZ. Первая точка основания имеет координаты A1=(0, r, 0). Тогда координаты остальных точек снования будем находить по следующей формуле:
Ai+1= Ai*ПоворотOZ(360/5), (4.12)
а координаты вершины конуса будут равны (0, 0, h).
Вид геометрической модели пирамиды с пятиугольным основанием приведен на рисунке 4.7.
| X |
| Z |
| Y |
| Ai |
| (0, 0, h) |
Рисунок 4.7 – Вид геометрической модели пирамиды с пятиугольным основанием
4.9 Геометрическая модель усечённой пирамиды с трёугольным основанием
Данный объект задаётся тремя параметрами: высота, радиус окружности, в которую вписано нижнее основание и радиус окружности, в которую вписано верхнее основание. Обозначим эти параметры соответственно буквами h, r1 и r2.
Пусть центр нижнего основания совпадает с началом локальной системы координат, а часть пирамиды без этого основания находится со стороны положительного направления оси OZ. Первая точка нижнего основания имеет координаты A11=(0, r1, 0), а первая точка верхнего основания A21=(0, r2, h). Тогда координаты остальных точек нижнего снования будем находить по следующей формуле:
A1i+1= A1i*ПоворотOZ(360/3), (4.13)
а координаты точек верхнего основания – по формуле:
A2i+1= A2i*ПоворотOZ(360/3). (4.14)
Вид геометрической модели усеченной пирамиды с треугольным основанием приведен на рисунке 4.8.
| z |
| x |
| y |
| A2i |
| A1i |
Рисунок 4.8 – Геометрическая модель усечённой пирамиды с трёугольным основанием
4.10 Моделирование икосаэдра
Для построения икосаэдра (рис. 4.9) используется цилиндр радиуса R, ось Z которого совпадает с осью цилиндра, а основание находится друг от друга на расстоянии ± h/2.

Рисунок 4.9 Построение икосаэдра
Каждое из окружностей оснований разбивается на 5 равных сегментов, и точки окружности последовательно соединяются между собой. Вращаясь против часовой стрелки на угол φ = 2*π /5, выбираются точки на первой и на второй окружности соответственно.
На высоте:  выбираются вершины P'0 и P''0 и соединяются с вершинами в основании (верхнего и нижнего соответственно).
выбираются вершины P'0 и P''0 и соединяются с вершинами в основании (верхнего и нижнего соответственно).
Остальные вершины получаются с помощью матрицы поворота:
P’i= P’i-1*Поворот(2*π /5) (4.1)
P" i= P”i-1*Поворот(2* π /5) (4.2)
Модель построенного икосаэдра изображена на рисунке 4.10.

Рисунок 4.10 – Модель икосаэдра
4.11 Геометрическая модель додекаэдра
Построение додекаэдра осуществляется при помощи икосаэдра.
Ниже приведены краткие шаги данной операции.
1. Построение икосаэдра;
2. Определение геометрических центров каждой из граней;
3. Соединение геометрических центров.
Для построения икосаэдра используется цилиндр единичного радиуса R, ось которого совпадает с осью OZ, и основание находится соответственно на высоте 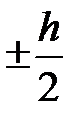 . Каждая из окружностей разбивается на 5 равных сегментов, и точки на окружности последовательно соединяются между собой.
. Каждая из окружностей разбивается на 5 равных сегментов, и точки на окружности последовательно соединяются между собой.
Двигаясь против часовой стрелки с шагом α =2π /n, выбираются точки то на одной, то на другой окружности. Далее происходит попарно соединение точек. На высоте  берется окончательная вершина.
берется окончательная вершина.
В графической базе данных додекаэдр можно представить в виде:
Додекаэдр(W), (4.15)
где w – длина стороны.
На рисунке 4.11 изображена геометрическая модель додекаэдра.
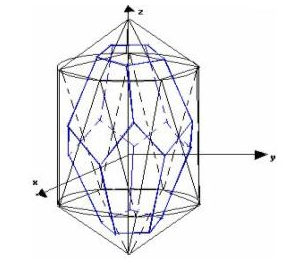
Рисунок 4.11 – Геометрическая модель додекаэдра
5 ПОШАГОВОЕ ПОСТРОЕНИЕ МОДЕЛИ СЛОЖНОГО ОБЪЕКТА
5.1 Декомпозиция сложного объекта
Моделью сложного трехмерного объекта, согласно заданию, является модель робота-краба, которая состоит из таких базовых примитивов как: эллипсоид, икосаэдр, призма с треугольным основанием, сфера, косоугольный цилиндр, усеченная пирамида с треугольным основанием, полусфера, косоугольная призма с треугольным основанием.
Модель робота-краба состоит из лап (призма с треугольным основанием, икосаэдр, усеченная пирамида с треугольным основанием), лап (косоугольный цилиндр) с клещнями (косоугольная призма с теугольным основанием), глаз (сфера), тело (полусфера, элипсоид).
5.2 Параметрические модели примитивов
Лапа состоит из следующих примитивов:
- призма с треугольным основанием Prizm3(r1, h1);
- икосаэдр Iko(r2);
- усеченная пирамида с треугольным основанием Piramid3(r3, r4, h2,).
Лапа с клещами состоит из следующих примитивов:
- косоугольный цилиндр Cyl(r5, h3, n1, m1)*M(сдвига);
- косоугольная призма с теугольным основанием KosPr(r6, h4)* *M(сдвига).
Глаз состоит из следующих примитивов:
- сфера Sphere (r7, n2, m2).
Тело состоит из следующих примитивов:
- полусфера Halfsphere(r8, n3, m3)*M(отсечения);
- элипсоид Elips(r9, n4, m4)*M(сжатия),
где r(i) – радиус, h(i) – высота, n(i), m(i) - число разбиения, М – матрица.
n1=n2=n3=n
m1=m2=m3=m
Запишем значения параметром фигур через r7:
h1=20*r7;
h2=r7;
h3=18*r7
h4=4*r7
r1=1.5*r7;
r2=r7;
r3=r7;
r4=2*r7;
r5=1.5*r7;
r6=1.5*r7;
r8=9*r7
r9=12*r7;
5.3 Пошаговое построение сложного объекта
Строим тело:
- Стоим элипосид:
Строим сферу радиусом 12*r7, умножаем на матрицу сжатия М(0.8, 1, 0.25), получаем элипсоид (рисунок 5.1).
| X |
| Y |
| Z |

Рисунок 5.1 – Эллипсоид
Строим полусферу:
- cтроим сферу радиусом 9*r7. Отсекаем пол сферу по оси –OZ.
Полученная фигура будет телом (рисунок 5.2).
| -X |
| Y |
| Z |

Рисунок 5.2- Тело
Строим глаза:
1 глаз:
- cтроим сферу радиусом r7. Переносим на (4*r7, 3*r7, 8*r7);
2 глаз:
- строим сферу радиусом r7. Переносим на (-4*r7, 3*r7, 8*r7).
Полученная фигура будет телом с глазами (рисунок 5.3)
| Z |
| Y |
| -X |

Рисунок 5.2- Тело с глазами
Строим лапы:
- строим призму с треугольным основанием:
- строим цилиндр с числом разбиения равным 3, радиуса 1.5*r7 и высотой 20*r7;
- строим икосаэдр
строим икосаэдр радиусом r7 и перемещаем на (0, 0, 20*r7);
- строим усеченную призму с треугольным основанием:
строим цилиндр с числом разбиения равным 3, радиусами r7, 2*r7 и высотой r7, поворачиваем вокруг оси OY на -90 градусов, перемещаем на (0, 0, 3*h-2/5h).
1 лапа:
- поворачиваем построенные фигуры на 90 градусов вокруг оси OX и 45 градусов вокруг оси OZ;
2 лапа:
- поворачиваем построенные фигуры на 90 градусов вокруг оси OX и -45 градусов вокруг оси OZ;
3 лапа:
- поворачиваем построенные фигуры на -90 градусов вокруг оси OX и 45 градусов вокруг оси OZ;
4 лапа:
- поворачиваем построенные фигуры на -90 градусов вокруг оси OX и -45 градусов вокруг оси OZ;
Полученная фигура будет содержать лапы (рисунок 5.3)
| -X |
| Z |
| Y |

Рисунок 5.3 - Фигура с лапами
Строим лапы с клещнями:
- строим косоугольный цилиндр:
- строим цилиндр радиусом 1.5*r7, высотой 20*r7, сдвигаем по оси OY на 0.1*r7
- строим косоугольную призму с треугольным основанием:
- строим цилиндр с числом разбиения равным 3, радиусом 1.5*r7, высотой 18*r7, сдвигаем по оси OX на 0.1*r7, перемещаем на 4*r7;
- Поворачиваем полученные фигуры на 90 градусов вокруг оси OX.
1 лапа с клещней:
- поворачиваем полученные фигуры на 30 градусов вокруг оси OY;
2 лапа с клещней:
- поворачиваем полученные фигуры на -30 градусов вокруг оси OY.
Получили робота-краба (рисунок 5.4)
| -X |
| Z |
| Y |
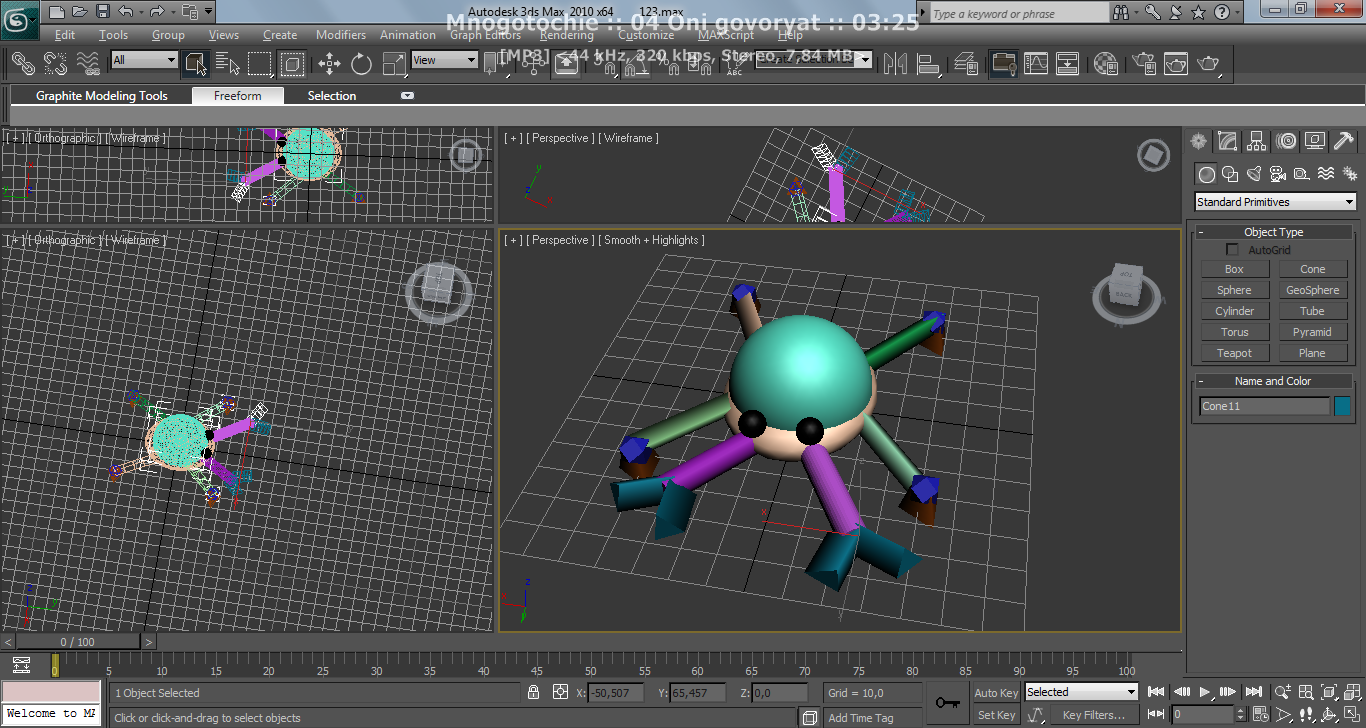
Рисунок 5.4 - Робот-краб
6 ОПИСАНИЕ ПРОГРАММНОЙ РЕАЛИЗАЦИИ
6.1 Структуры данных для хранения параметрических объектов
В данном курсовом проекте описаны классы, упрощающие работу с 3D-примитивами, информационной частью данных классов являются структуры данных, хранящие параметры объектов. Иерархия данных классов описывается диаграммой на рисунке 6.1.
| OBJECT3D int color[4]; float position[3]; int material; int modeltype; int n, m; |
| SPHERE float radius; |
| HALFSPHERE float radius; |
| IKO float riblen; |
| CYL float height; float radius; |
| ELIPS float radius; |
| PIRAMID3 float height; float radius1; float radius2; |
| KOSPR float height; float radius; float shift; |
| PRISM3 float height; float radius; |
Рисунок 6.1 – Иерархия классов, содержащих параметры объектов сцены
6.2 Структуры данных для камеры
В реализуемом программном продукте структура данных для камеры описывается на языке C++ следующим образом:
struct
{
float posx, posy, posz;
float dirx, diry, dirz;
}settings, где
posx, posy, и posz –соответственно координаты наблюдателя, а dirx, diry, dirz – соответственно координаты направляющего вектора.
6.3 Структуры данных для источников света
В реализуемом программном продукте структура данных для источников света описывается на языке C++ следующим образом:
struct
{
float pos[4];
float dir[3];
float color[4];
int lightmodeltype;
bool shining;
} settings, где
pos – массив координат источника света, dir – массив координат напрвляющего вектора, color – массив, содержащий цвет излучаемого света в формате RGBA, lightmodeltype – тип источника света (точечный, удалённый, цилиндрический), shining – признак включенности источника света.
Выше приведена структура данных заключена в класс, написанный для облегчения работы с источниками света, имеющий следующий протокол
class LIGHT
{
struct{
float pos[4];
float dir[3];
float color[4];
int lightmodeltype;
GLboolean shining;
} settings;
int index;
public:
void Draw();
GLenum GetIndex();
bool Shining();
LIGHT& TurnOn();
LIGHT& TurnOff();
LIGHT(int gllight): index(gllight);
~LIGHT(){glDisable(index); }
void SetLightModelType(int lmt);
void Dispose(float PosX, float PosY, float PosZ, float PosT);
LIGHT& Direct(float DirX, float DirY, float DirZ);
LIGHT& SetColor(float r, float g, float b);
void GetPosition(float *x, float *y, float *z);
void GetDirection(float *x, float *y, float *z);
void GetColor(float *r, float *g, float *b);
};
6.4 Описание внутреннего формата графической БД
Графическая база данных реализуемого программного продукта организована в виде набора структур данных, содержащих параметры графических примитивов, камеры и источников. К операциям, осуществимым над графической базой данных, относятся добавление, удаление и поиск графических примитивов, а также изменение их параметров.
6.5 Описание формата файла хранения сцены
Файл, содержащий параметры сцены имеет формат, показанный на таблице 6.1.
Таблица 6.1 – Описание формата файла хранения сцены
| Название блока | Размер блока в байтах |
| Параметры графических примитивов | |
| Параметры источников света | |
| Параметры камеры | |
| Матрица модельно-видовых преобразований | |
| Параметры интерфейса программы |
Размер файла хранения сцены составляет 911 байт.
6.6 Описание программных моделей
Для удобства построения системы трехмерного графического моделирования программа была разбита на следующие модули:
- KP.cpp – главный программный модель;
- globals.h – файл, содержащий описание глобальных переменных, доступных из всех программных модулей;
- glsetup.h – файл, содержащий подпрограммы, служащие для установки матриц проекций и областей просмотров;
- primitives.h – файл, содержащий описание протоколов и реализации классов, упрощающих работу с графическими примитивами;
- light.h – файл, содержащий описание протоколов и реализации классов, упрощающих работу с источниками света;
- camera.h – файл, содержащий описание протокола и реализацию классоа, упрощающего работу с камерой;
- drawscene.h - файл, содержищий подпрограммы отрисовки сцены;
- mainwnd.h - файл, содержищий описание функций для работы с главным окном программы;
- panel.h – файл, содержищий описание функций для работы с панелью управления в главном окне программы;
- panel_aff_aj.h, panel_camera.h, panel_light.h, panel_primitives.h, panel_scene.h – модули, касающиеся построения интерфейса программы, содержащие реализацию подпрограмм, описывающих поведение диалоговых панелей, позволяющих пользователю изменять параметры камеры, графических примитивов, источников света и сцены, а также осуществлять аффинные преобразования.
Взаимосвязь программных модулей показана на рисунке 6.2.
| KP.cpp |
| globals.h |
| primitives.h |
| panel.h |
| light.h |
| camera.h |
| scene.h |
| glsetup.h |
| mainwnd.h |
Рисунок 6.2 - Взаимосвязь программных модулей
6.7 Описание основных процедур и функций
Программный продукт, реализуемый в данном курсовом проекте, разбит на функции следующих категорий:
1) функции настройки графического вывода:
- void glSetViewport(int vp). Устанавливает область вывода. vp – параметр, задающий область вывода, которую необходимо установить;
- void SetOrtho(). Устанавливает ортографическую проекцию;
- void SetIso(). Устанавливает изометрическую проекцию.
2) Функции отрисовки графических примитивов и визуализации источников света:
- void SPHERE:: Draw(). Функция отрисовки сферы;
- void HALFSPHERE:: Draw(). Функция отрисовки полусферы;
- void CUBE:: Draw(). Функция отрисовки куба;
- void PRISM5:: Draw(). Функция отрисовки пятигранной пизмы;
- void PRISM3:: Draw(). Функция отрисовки трёхгранной призмы;
- void PIRAMID:: Draw(). Функция отрисовки пирамиды с пятиугольным основанием;
- void PIRAMID3:: Draw(). Функция отрисовки усечённой пирамиды с трёхугольным основанием;
- void CONE:: Draw(). Функция отрисовки косоугольного конуса;
- void LIGHT:: Draw(). Функция визуализации источника света.
- void DrawAxes().Функция отрисовки координатных осей;
- void DrawScene(). Функция отрисовки всей сцены.
3) функции сохранения-зугрузки параметров сцены:
- void SaveScene(char *fn). Сохраняет в файл с именем, заданным аргументом fn, параметры сцены;
- void LoadScene(char *fn). Загружает параметры сцены из файла с именем, заданным аргументом fn;
4) функции построения графического интерфейса:
- void ShowHelp(). Данная функция загружает текст справки из файла и выводит в его во всплывающем окне;
- void InitMainWindow(HINSTANCE hInstance, char *caption, int wdth). Инициализирует главное окно программы. hInstance – экземпляр приложения, caption – заголовок главного окна, width – ширина главного окна;
- void InitPanel(HINSTANCE hInstance). Инициализирует окно панели управления. hInstance – экземпляр приложения;
- void ShowSeparators(int cmd). Функция показа-скрытия разделителей окон проекций. cmd – аргумент, значением которого определяется выполняемое действие (показ или скрытие).
6.8 Описание использованных функций OpenGL
1. Функции аффинного преобразования в пространстве:
- glRotatef(float a, float x, float y, float z) – поворот. a – угол поворота, x, y, z – координаты вектора, вокруг которого осуществляется вращение;
- glScalef(float x, float y, float z) – масштабирование. x, y и z –коэффициенты масштабирования соответственно по осям Ox, Oy и Oz;
- glTranslatef(float x, float y, float z) – перенос. x, y, z – коеффициенты, задающие расстояние, на которое происходит перемещение по осям Ox, Oy и Oz.
2. Функции проецирования:
- glViewPort(x, y, width, height) – устанавливает область вывода, заданную переменными x, y, width и height;
- glOrtho(Xmi, Xma, Ymi, Yma, Zmi, Zma) – ортографическая проекция. Xmi, Xma, Ymi и Yma, Zmi, Zma – координаты противолежащих углов параллелепипеда;
3. Функции для работы с камерой:
- glLookAt(ex, ey, ez, lx, ly, lz, x, y, z) – задает позицию и направление камеры. ex, ey, ez – координаты наблюдателя, lx, ly, lz – точка наблюдения, x, y, z – координаты вектора главной оптической оси камеры.
4. Функции для работы со светом:
- glLight(light, pname, param) – задает параметры источнику света;
- glLightModelf(pname, param) – задает модель освещения. Pname - имя параметра модели освещения, param – устанавливаемое значение.
5. Функции удаления невидимых граней:
- glEnable(DEPTH_TEST) – включает тест глубины;
- glDisable(DEPTH_TEST) – выключает тест глубины;
- glDepthFunc(func) – устанавливает функцию глубины;
- glClearDepth(dep) – очищает буфер глубины;
- glDepthRange(Zn, Zf) – задает диапазон глубины.
6. Функции работы с матрицами:
- glLoadMatrixf(float *matr) – устанавливает в качестве текущей матрицы matr;
- glMultMatrixf(float *matr) – умножает текущую матрицу на matr;
- glLoadIdentity() – делает текущую матрицу единичной;
- glMatrixMode(int matr) – задаёт текущую матрицу.
7. Функции получения переменных состояния:
- glGetFloatf(float *v) – получение значения переменной типа float;
8. Функции заания значений переменных состояния булевого типа:
- glEnable(int param) – установка переменной, заданной параметром pname, в true;
- glDisable(int param) – установка переменной, заданной параметром pname, в false.
6.9 Реализация аффинных преобразований
В программе графического моделирования пользователю предоставляется возможность выполнения пяти видов аффинных преобразований: перенос, вращение, масштабирование, сдвиг и отражение. Причём, задание параметров каждого из преобразований производится пользователем. Все аффинные преобразования производятся над всеми примитивами одновременно.
Преобразования переноса, поворота и масштабирования производятся путём вызова функций OpenGL, соответствующих этим преобразованиям (glTranslate, glRotate и glScale), а преобразования отражения и сдвига – путём умножения матрицы модельно-видового преобразования на матрицу соответствующего аффинного преобразования, путём вызова функции OpenGL glMultMatrix.
6.10 Описание структуры программы в виде блок-схемы
Структура работы программы отражена диаграммой состояний на рисунке 6.3.
| Запуск программы |
| Проверка очереди событий |
| Нет событий для обработки |
| Прорисовка объектов из списка прорисовки |
| Прорисовка завершена |
| Запрос на загрузку сцены |
| Чтение файла состояния сцены |
| Загрузка завершена |
| Запрос на загрузку сцены |
| Чтение файла состояния сцены |
| Сохранение завершено |
| Ошибка |
| Ошибка |
| Выдача сообщения об ошибке ввода-вывода |
| Запрос на добавление объекта |
| Добавление объекта в список прорисовки |
| Запрос на удаление объекта |
| Удаление объекта из списка прорисовки |
| Добавление завершено |
| Удаление завершено |
| Запрос на изменение параметров объекта |
| Изменение параметров объекта |
| Изменение завершено |
| Запрос на изменение параметров камеры |
| Изменение параметров камеры |
| Изменение завершено |
| Изменение параметров источников света |
| Изменение завершено |
| Запрос на изменение параметров источников света |
| Запрос на выход из программы |
| Закрытие контекста OpenGL, уничтожение всех окон, завершение цикла обработки сообщений. Завершение работы программы |
Рисунок 6.3 - Дианрамма состояний
7 ПРОВЕДЕНИЕ ТЕСТОВЫХ ИСПЫТАНИЙ
Проведение тестовых испытаний заключалось в следующем:
- тестирование работы алгоритмов аффинных преобразований над заданной моделью робота-краба и базовых примитивов (см. рис., В14, В12);
- тестирование камеры и источников света (см. рис. В.10, В.11, В.13);
- тестирование прорисовки заданных примитивов (см. рис. В.2-В.9);
- тестирование открытия и сохранения сцены;
- сравнение фигуры построенной фигуры (В.14) с ее моделью (А1).
ЗАКЛЮЧЕНИЕ
В результате работы над курсовым проектом была создана интерактивная система трехмерного графического моделирования в пространстве таких объектов как: сфера, полусфера, икосаэдр, призма с треугольным основанием, усеченная пирамида с треугольным основанием, косоугольная призма с треугольным основанием, эллипсоид, косоугольный цилиндр. В ходе реализации проекта были рассмотрены аффинные преобразования как методы выполнения преобразований над объектами в пространстве. Реализована возможность сохранение сцены в файл. Результаты тестирования показали, что программа удовлетворяет предъявленным в постановке задания требованиям.
В дальнейшем КП может быть модернизирован и улучшен в соответствии с нововведенными требованиями.
Список использованной литературы
1. Курс лекций.
2. Френсис Хилл. OpenGL. Программирование компьютерной графики. Для профессионалов. – Спб.: Питер, 2002. – 1088 с.: ил.
3. Девис Т., Нейдер Дж., Шрайнер Д. OpenGL. Руководство по программированию. Юиюлиотека программиста. 4-е издание.- СПб: Питер, 2006 -624с.
4. Выгодский М.Я. Справочник по высшей математике.– М.: Наука, 1964. – 872с.: ил.
5. Баяковский Ю.М., Игнатенко А.В. Начальный курс OpenGL.М.: «Планета Знаний», 2007. – 221с.
6. Шикин А.В. Боресков А.В. Компьютерная графика. Динамика, реалистические изображения. – М.: ДИАЛОГ-МИФИ, 1996. – 288с.
7. Препарата Ф., Шеймос М. Вычислительная геометрия: Введение: Пер. с англ. - М.: Мир, 1989.-478с.
8. Эгрон Жерар. Синтез изображений. Базовые алгоритмы.: пер. с франц. А.В.Серединского. М.: Радио и связь, 1993. 216с. библ.-44, рус.библ.-5.
9. Rogers, D. 1998. Procedural Element for Computer Graphics. New York: McGraw-Hill;
10. Yaglom, I.M. 1962 Geometric Transformations. Toronto. Random House.
11. FAQ по программированию OpenGL https://faqs.org.ru [opengl.txt]
Приложение А