Доказательство. Подставив функцию в уравнение (6.5), получим

Подставив функцию в уравнение (6.5), получим

f₁ + f₂. Это равенство является тождеством, т.к. f₁ и f₂. Теорема доказана.

4. Решение уравнения 2-го порядка с постоянными коэффициентами со специальной правой частью.

Пусть в уравнении (6.1) коэффициенты постоянны, т.е. уравнение имеет вид:

f(x) (7.1)

где .

Рассмотрим метод отыскания частного решения уравнения (7.1) в случае, когда правая часть f(x) имеет специальный вид. Это метод называется методом неопределенных коэффициентов и состоит в подборе частного решения в зависимости от вида правой части f(x). Рассмотрим правые части следующего вида:

f(x) , где – многочлен степени , причем некоторые коэффициенты, кроме , могут равняться нулю. Укажем вид, в котором надо брать частное решение в этом случае.

Если число не является корнем характеристического уравнения для уравнения (5.1), то частное решение записываем в виде: , где – неопределенные коэффициенты, которые подлежат определению методом неопределенных коэффициентов.

Пример 1. Найти общее решение уравнения .

Решение.

Для уравнения составляем характеристическое уравнение: . Откуда получаем , . Следовательно, общее решение однородного уравнения есть . Правая часть заданного уравнения f(x) имеет специальный вид (случай 1), причем 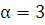не является корнем характеристического уравнения, поэтому частное решение ищем в виде: , где – неопределенные коэффициенты. Найдем производные первого и второго порядков и подставим их в заданное уравнение:

.

Обе части сокращаем на и приравниваем коэффициенты при одинаковых степенях в левой и правой частях равенства

Из полученной системы уравнений находим: . Тогда , а общее решение заданного уравнения есть:

.

Если является корнем кратности соответствующего характеристического уравнения, то частное решение ищем в виде:

,

где – неопределенные коэффициенты.

5. Метод вариации произвольных постоянных (метод Лагранжа).

Непосредственное нахождение частного решения лнду, кроме случая уравнения с постоянными коэффициентами, причем со специальными свободными членами, представляет большие трудности. Поэтому для нахождения общего решения лнду обычно применяют метод вариации произвольных постоянных, который всегда дает возможность найти общее решение лнду в квадратурах, если известна фундаментальная система решений соответствующего однородного уравнения. Этот метод состоит в следующем.

Согласно вышеизложенному, общее решение линейного однородного уравнения:

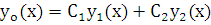, (8.1)

где – линейно независимые на некотором интервале X решения лоду, а 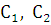- произвольные постоянные. Будем искать частное решение лнду в форме (8.1), считая, что 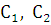– не постоянные, а некоторые, пока неизвестные, функции от :

. (8.2)

Продифференцируем равенство (8.2):

. (8.3)

Подберем функции и так, чтобы выполнялось равенство: . Тогда вместо (8.3) будем иметь:

. (8.4)

Продифференцируем это выражение еще раз по . В результате получим:

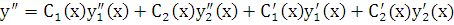. (8.5)

Подставим (8.2), (8.4), (8.5) в лнду 2-го порядка f(x):

f(x)

или

f(x). (8.6)

Так как - решения лоду , то последнее равенство (8.6) принимает вид: f(x).

Таким образом, функция (8.2) будет решением лнду в том случае, если функции и удовлетворяют системе уравнений:

(8.7)

Так как определителем этой системы является определитель Вронского для двух линейно независимых на X решений соответствующего лоду, то он не обращается в ноль ни в одной точке интервала X. Следовательно, решая систему (8.7), найдем и : и . Интегрируя, получим:

, ,

где - произвольные постоянные.

Возвращаясь в равенство (8.2), получим общее решение неоднородного уравнения:

.

Пример. Решить уравнение: .

Решение.

Соответствующее однородное уравнение . Интегрируя его, получим общее решение: . Итак, двумя линейно независимыми решениями, образующими общее решение, являются функции и .

Предположим теперь, что общим решением заданного уравнения является выражение .

Для определения функций и имеем систему уравнений:

Откуда получаем , 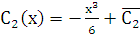. Следовательно, общее решение заданного уравнения есть: .