
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Изохорный
|
|
В изохорном процессе постоянен объём, то есть  . Элементарная работа газа равна произведению изменения объёма на давление, при котором происходит изменение (
. Элементарная работа газа равна произведению изменения объёма на давление, при котором происходит изменение ( ). Первое Начало Термодинамики для изохорного процесса имеет вид:
). Первое Начало Термодинамики для изохорного процесса имеет вид:

А для идеального газа

Таким образом,

где  — число степеней свободы частиц газа.
— число степеней свободы частиц газа.
Другая формула:  , где γ — показатель адиабаты, R — универсальная газовая постоянная.
, где γ — показатель адиабаты, R — универсальная газовая постоянная.
10.
1. Обратимым термодинамическим процессом называется термодинамический процесс, допускающий возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения.
Необходимым и достаточным условием обратимости термодинамического процесса является его равновесность.
2. Необратимым термодинамическим процессом называется термодинамический процесс, не допускающий возможности возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения.
Все реальные процессы протекают с конечной скоростью. Они сопровождаются трением, диффузией и теплообменом при конечной разности между температурами системы и внешней среды. Следовательно, все они неравновесны и необратимы.
11.
Круговой процесс — процесс, при котором газ, пройдя через ряд состояний, возвращается в исходное.
Если круговой процесс на диаграмме P-V протекает по часовой стрелке, то часть тепловой энергии, полученной от нагревателя, превращается в работу. Так работает тепловая машина.
Если круговой процесс на диаграмме P-V протекает против часовой стрелки, то тепловая энергия передается от холодильника (тела с меньшей температурой) к нагревателю (телу с большей температурой) за счет работы внешней силы. Так работает холодильная машина.

Коэффициент полезного действия тепловой машины равен отношению работы  за цикл к полученной от нагревателя тепловой энергии
за цикл к полученной от нагревателя тепловой энергии  :
:
 .
.
Холодильный коэффициент холодильной машины равен отношению тепловой энергии  , отобранной от холодильника за цикл, к затраченной работе
, отобранной от холодильника за цикл, к затраченной работе  :
:
 .
.
Цикл Карно — круговой процесс, состоящий из двух изотерм и двух адиабат.
Коэффициент полезного действия (кпд) цикла Карно — отношение суммарной работы за цикл к полученному теплу:
 .
.
Таким образом, кпд цикла Карно всегда меньше единицы (100%) и зависит только от соотношения температур холодильника и нагревателя
12.
Для характеристики рассеяния энергии вводится понятие энтропии. (Величина энтропии характеризует тепловое состояние системы и определяет вероятность осуществления данного состояния тела. Чем более вероятно данное состояния, тем больше энтропия.) Все естественные процессы сопровождаются ростом энтропии. Энтропия остается постоянной только в случае идеализированного обратимого процесса, происходящего в замкнутой системе, то есть в системе, в которой не происходит обмен энергией с внешними по отношению к этой системе телами.
Энтропия и ее термодинамический смысл:

Энтропия – это такая функция состояния системы, бесконечно малое изменение которой в обратимом процессе равно отношению бесконечно малого количества теплоты, введенного в этом процессе, к температуре, при которой оно вводилось.
В конечном обратимом процессе изменения энтропии может быть подсчитано по формуле:

где интеграл берется от начального состояния 1 системы до конечного состояния 2.
Поскольку энтропия есть функция состояния, то свойством интеграла  является его независимость от формы контура (пути), по которому он вычисляется, следовательно, интеграл определяется только начальным и конечным состояниям системы.
является его независимость от формы контура (пути), по которому он вычисляется, следовательно, интеграл определяется только начальным и конечным состояниям системы.
- В любом обратимом процессе изменения энтропии равно 0
 (1)
(1)
- В термодинамике доказывается, что S системы совершающей необратимой цикл возрастает
Δ S > 0 (2)
Т.к. для адиабатического процесса δ Q = 0, то Δ S = 0 => S = const, то есть адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его называют изоэнтропийным.
При изотермическом процессе (T = const; T 1 = T 2:  )
)

При изохорном процессе (V = const; V 1 = V 2;  )
)
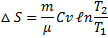
второеначало термодинамики можно сфор- мулировать как закон возрастания энтропии замкнутой системы при нео-братимых процессах: любой необрати-мый процесс в замкнутой системе про-исходит так, что энтропия системы при этом возрастает. Можно дать более краткую форму-лировку второго начала термодинами-ки: в процессах, происходящих в замкну-той системе, энтропия не убывает.

13.Уравнение Ван-дер-Ваальса и его изотермы
физик И.Ван-дер-Ваальс (1837—1923) вывел уравне-ние состояния реального газа. Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.
1. Учет собственного объема моле-кул. Наличие сил отталкивания, кото-рые противодействуют проникновению в занятый молекулой объем других мо-лекул, сводится к тому, что фактический
свободный объем, в котором могут дви-гаться молекулы реального газа, будетне Vm, a Vm - b, где Ь — объем, занимае-мый самими молекулами. Объем Ь равен
учетверенномусобственномуобъемумо-лекул. Если, например, в сосуде находят-ся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диа-метра с? молекулы. Это означает, что для центров обеих молекул оказывается не-доступным сферический объем радиу-са d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в расчете на одну молекулу.
2. Учет притяжения молекул. Дей-ствие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним дав-лением. По вычислениям Ван-дер-Ва-альса, внутреннее давление обратно пропорционально квадрату молярного объема:
(61.1)
где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолеку-лярного притяжения; Vm — молярный объем.
Вводя эти поправки, получим урав-нение Ван-дер-Ваальса для 1 моль газа
{уравнение состояния реальных га-зов):
14. Поверхностное натяжение
Поверхностное натяжение – сила, возникающая на поверхностираздела двух фаз и стремящаяся сократить поверхность до возможного минимума.
Силы, действующие со стороны выделенного участка на граничащие с ним участки, совершают работу
где/— сила поверхностного натяжения, действующая на единицу длины конту-ра поверхности жидкости.
Из рис. 99 видно, что,
(66.2)
Эта работа совершается за счет уменьшения поверхностной энергии, т.е.
(66.3)
Из сравнения выражений (66.1) — (66.3) видно, что
(66.4)
т. е. поверхностное натяжение равно силе поверхностного натяжения, при-ходящейся на единицу длины контура, ограничивающего поверхность.
15.смачивание— физическое взаимодействие жидкости с поверхностью твёрдого тела или другой жидкости. Смачивание бывает двух видов:
· Иммерсионное (вся поверхность твёрдого тела контактирует с жидкостью)
· Контактное (состоит из трёх фаз — твердая, жидкая, газообразная)
Смачивание зависит от соотношения между силами сцепления молекул жидкости с молекулами (или атомами) смачиваемого тела (адгезия) и силами взаимного сцепления молекул жидкости (когезия).
Если жидкость контактирует с твёрдым телом, то существуют две возможности:
1. молекулы жидкости притягиваются друг к другу сильнее, чем к молекулам твёрдого тела. В результате силы притяжения между молекулами жидкости собирают её в капельку. Так ведёт себя ртуть на стекле, вода на парафине или «жирной» поверхности. В этом случае говорят, что жидкость не смачивает поверхность;
2. молекулы жидкости притягиваются друг к другу слабее, чем к молекулам твёрдого тела. В результате жидкость стремится прижаться к поверхности, расплывается по ней. Так ведёт себя ртуть на цинковой пластине, вода на чистом стекле или дереве. В этом случае говорят, что жидкость смачивает поверхность.
Степень смачивания характеризуется углом смачивания. Угол смачивания (или краевой угол смачивания) — это угол, образованный касательными плоскостями к межфазным поверхностям, ограничивающим смачивающую жидкость, а вершина угла лежит на линии раздела трёх фаз. Измеряется методом лежащей капли[1].
16.капиллярные явления-совокупность явлений, обусловленных действием межфазового поверхностного натяжения на границе раздела несмешивающихся сред. Явления в жидкости, вызванные искревлением их поверхности, граничащие с другой жидкостью, газом или паром.