
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 15 № 250995.
|
|
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см  1 см (см. рис.). В ответе запишите
1 см (см. рис.). В ответе запишите  .
.

Ответ: 2
45. Задание 15 № 27381. 
В треугольнике  угол
угол  равен 90°,
равен 90°,  ,
,  . Найдите косинус внешнего угла при вершине
. Найдите косинус внешнего угла при вершине  .
.
Ответ: -0, 5
46. Задание 16 № 509681.  Даны два шара с радиусами 4 и 1. Во сколько раз объём большего шара больше объёма другого?
Даны два шара с радиусами 4 и 1. Во сколько раз объём большего шара больше объёма другого?
Ответ: 64
47. Задание 16 № 506891. Даны два цилиндра. Радиус основания и высота первого равны соответственно 3 и 2, а второго — 8 и 9. Во сколько раз объём второго цилиндра больше объёма первого?
Ответ: 32
48. Задание 16 № 27088.  Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен 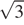 .
.
Ответ: 3
49. Задание 17 № 510923. На координатной прямой отмечены точки A, B, C, D (см. рисунок).
Число m равно  .
.

Установите соответствие между указанными точками и числами в правом столбце, которые им соответствуют.
| Точки | Числа | |
| А B C D | 1) m + 1
2) m 3
3)  4)
4) 
|
В приведенной ниже таблице под каждой буквой, обозначающей точку, укажите номер соответствующего ей числа.
| А | B | C | D |
Ответ: 3142
50. Задание 17 № 506360. Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
| ЧИСЛА | ОТРЕЗКИ | |
А)  Б)
Б)  В)
В)  Г)
Г) 
| 1) [0; 1] 2) [1; 2] 3) [2; 3] 4) [4; 5] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Ответ: 2314
51. Задание 17 № 506872. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
А)  Б)
Б)  В)
В)  Г)
Г) 
| 1)  2)
2)  3)
3)  4)
4) 
|
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
| А | Б | В | Г |
Ответ: 3412
52. Задание 18 № 507071. Если в маршрутном такси заняты все места, то оно трогается от остановки. Выберите утверждения, которые следуют из приведённых данных.
1) Если в маршрутке есть свободные места, то она не трогается
2) Если маршрутка продолжает стоять, то в ней остались свободные места
3) Если на каждом месте маршрутки сидит пенсионер, то она трогается от остановки
4) Если маршрутка отъехала от остановки, то в ней заняты все места
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: 23
53. Задание 18 № 510269. Среди дачников в посёлке есть те, кто выращивает виноград, и есть те, кто выращивает груши. А также есть те, кто не выращивает ни виноград, ни груши. Некоторые дачники в этом посёлке, выращивающие виноград, также выращивают и груши. Выберите утверждения, которые верны при указанных условиях.
1) Если дачник из этого посёлка не выращивает виноград, то он выращивает груши.
2) Среди тех, кто выращивает виноград, есть дачники из этого посёлка.
3) Есть хотя бы один дачник в этом посёлке, который выращивает и груши, и виноград.
4) Если дачник в этом посёлке выращивает виноград, то он не выращивает груши.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: 23
54. Задание 18 № 510249. Некоторые сотрудники фирмы летом 2014 года отдыхали на даче, а некоторые — на море. Все сотрудники, которые не отдыхали на море, отдыхали на даче. Выберите утверждения, которые верны при указанных условиях.
1) Каждый сотрудник этой фирмы отдыхал летом 2014 года или на даче, или на море, или и там, и там.
2) Сотрудник этой фирмы, который летом 2014 года не отдыхал на море, не отдыхал и на даче.
3) Если Фаина не отдыхала летом 2014 года ни на даче, ни на море, то она является сотрудником этой фирмы.
4) Если сотрудник этой фирмы не отдыхал на море летом 2014 года, то он отдыхал на даче.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: 14
55. Задание 19 № 510735. Найдите трёхзначное число A, обладающее всеми следующими свойствами:
· сумма цифр числа A делится на 5;
· сумма цифр числа (A + 4) делится на 5;
· число A больше 350 и меньше 400.
В ответе укажите какое-нибудь одно такое число.
Ответ: 357|366|389
56. Задание 19 № 506312. Трёхзначное число при делении на 10 даёт в остатке 3. Если последнюю цифру числа перенести в начало его записи, то полученное число будет на 72 больше первоначального. Найдите исходное число.
Ответ: 253
57. Задание 19 № 510992. Найдите трёхзначное натуральное число, которое при делении на 4 и 15 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите какое-нибудь одно такое число.
Ответ: 123|543|963
58. Задание 20 № 510036. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Кузнечик начинает прыгать из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков?
Ответ: 12
59. Задание 20 № 511016.  Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
Ответ: 12
60. Задание 20 № 506292. Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
Ответ: 117700