Соединения простых трубопроводов

Последовательное соединение. Пусть имеется несколько простых трубопроводов различной длины разного диаметра, с различным набором местных сопротивлений (рис. 6.4).

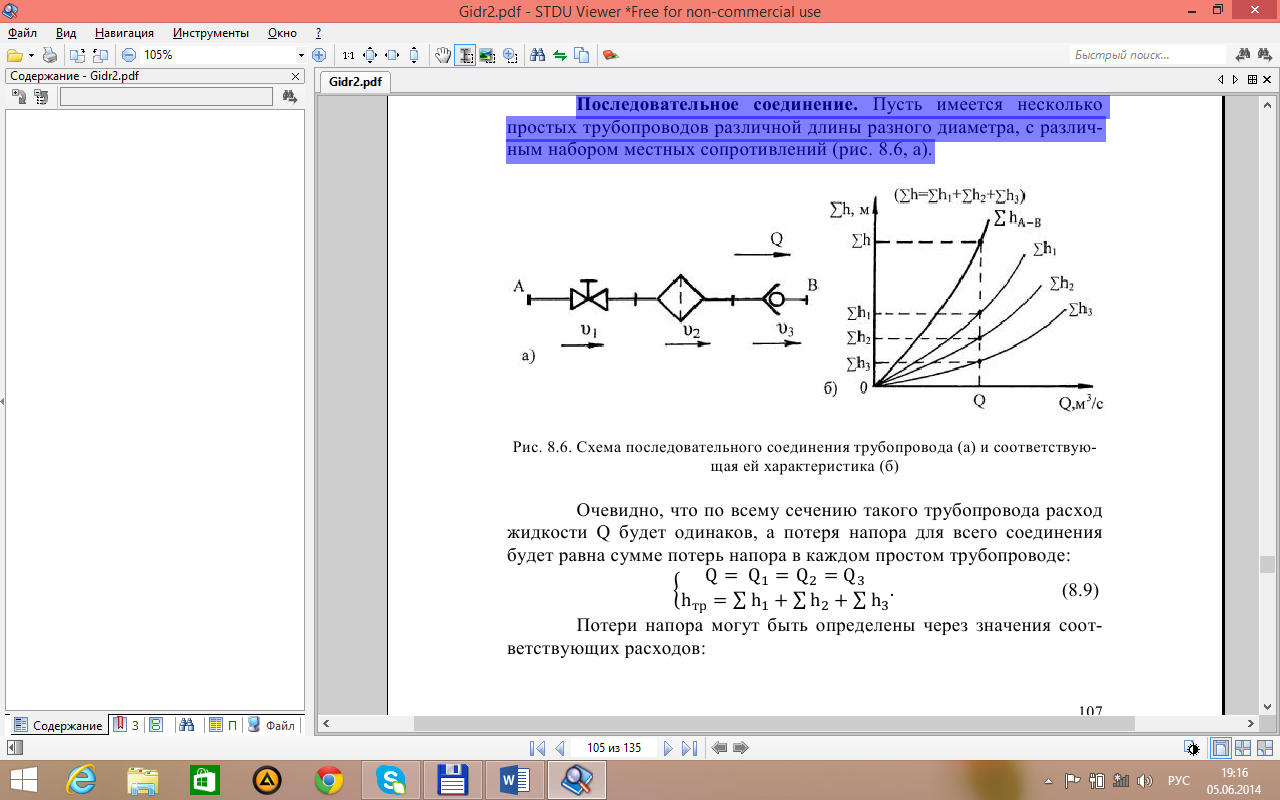
Рисунок 6.4 – Схема последовательного соединения трубопровода

Очевидно, что по всему сечению такого трубопровода расход жидкости Q будет одинаков, а потеря напора для всего соединения будет равна сумме потерь напора в каждом простом трубопроводе:

(6.2)

Потери напора могут быть определены через значения соответствующих расходов:

(6.3)

Совместное решение уравнений (6.2) и (6.3) является основной для расчета гидросистемы с последовательным соединением трубопроводов.

При графическом методе расчета строят суммарную характеристику соединения. Для этого строят характеристики простых трубопроводов по зависимостям (6.3), затем складывают по зависимости (6.2) (рис. 6.5).

Рисунок 6.5 – Характеристика последовательного соединения трубопровода

Параллельное соединение. Рассмотрим параллельное соединение нескольких простых трубопроводов (рис. 6.6).

Рисунок 6.6 – Схема параллельного соединения трубопроводов

Очевидно, что расход жидкости Q до точки А и после точки В один и тот же и равен сумме расходов в параллельных ветвях:

(6.4)

Потери напора в каждом из трубопроводов равны между собой:

(6.5)

Это следует из того, что 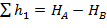; ; ; и объясняется распределением расходов Q ₁, Q ₂ и Q ₃ таким образом, что потери в параллельных ветвях трубопровода остаются равными.

Таким образом, совместное решение уравнений (6.4) и (6.5) позволяет рассчитать параллельное соединение простых трубопроводов.

Для получения суммарной характеристики параллельного соединения необходимо сложить расходы в исходных трубопроводах при одинаковых потерях напора (рис. 6.7).

Рисунок 6.7 – Характеристика параллельного соединения трубопровода