
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Суждения. Виды суждений.
|
|
Наряду с понятием к числу основных форм мышления относится суждение. Эта форма мышления является, по существу, обязательным элементом всякого познания, в особенности, связанного с процессами рассуждения, с осуществлением выводов и построением доказательств. В этой форме фиксируются результаты познания отдельных предметов, классов предметов, некоторых ситуаций вообще. В мысли этого типа содержится, с одной стороны, описание или хотя бы просто обозначение этих предметов, классов, ситуаций, а с другой - утверждение или отрицание наличия у них той или иной характеристики.
Пример. В суждении «Каждая планета Солнечной системы вращается вокруг своей оси» утверждается наличие в действительности ситуации: вращение вокруг своей оси каждой планеты Солнечной системы. А в суждении «Ни одна планета Солнечной системы не является неподвижной» отрицается наличие в действительности ситуации покоя каждой планеты Солнечной системы.
Суждение – это форма мысли, содержащая описание некоторой ситуации и утверждение или отрицание наличия этой ситуации в действительности.
Важнейший отличительный признак суждения – утверждение или отрицание чего-либо о чем-либо. В понятии ничего не утверждается и не отрицается. В нем лишь выделяется сам предмет мысли (например: «день», «ночь», «солнечный день», «несолнечный день»). В суждении же акцентируется внимание на самом соотношении между какими-либо предметами мысли: «День солнечный» или «День не солнечный», «День прошел», «Ночь настала».
И в самых простых, и в достаточно сложных суждениях всегда утверждается или отрицается наличие тех или иных признаков у некоторых объектов. Поэтому в общем виде определение суждения можно сформулировать и следующим образом:
Суждение – это мысль, в которой утверждается или отрицается наличие связи между объектами и признаками.
Знаком, в виде которого выражается суждение, является повествовательное предложение. Смыслом этого знака должна быть связанная с ним мысль. Это и есть само суждение. Что касается значения предложения, то иногда в качестве него рассматривают ситуацию, которая имеет или не имеет места в действительности и которая описывается суждением. Однако чаще всего значением предложения принято считать истину или ложь.
В современной логике вместо термина «суждение» предпочитают употреблять термин «высказывание». В традиционной логике термином «суждение» обозначали именно некоторый смысл повествовательного предложения с учетом того, что он может быть общим для различных знаковых форм. Иначе говоря, одно и то же суждение может быть выражено в различных формах повествовательных предложений.
Виды суждений. При выделении видов суждений, прежде всего, различают простые и сложные. Простым называется такое суждение, ни одна логическая часть которого не является суждением.
Пример. «Математика – абстрактная наука».
Сложным является такое суждение, которое содержит в качестве своей правильной части, т.е. части, не совпадающей с целым, некоторое другое суждение.
Пример. «Если вы будете хорошо учиться, то обязательно получите диплом».
Виды простых суждений. Основными частями простых суждений являются один или несколько субъектов суждения (логических подлежащих) и предикат суждения (логическое сказуемое). Субъект и предикат суждения называются терминами этого суждения.
Субъект суждения – это термин, возможно, выражающий понятие и представляющий предмет, о котором нечто утверждается или отрицается. Субъект суждения принято обозначать буквой S.
Предикат суждения – часть суждения, выражающая то, что утверждается или отрицается о предметах, которые представляют субъекты. Предикат обозначается буквой Р.
Пример. В суждении «Солнце есть раскаленное небесное тело» субъект – «Солнце», предикат – «раскаленное небесное тело». В суждении «Земля вращается вокруг Солнца» два субъекта – «Земля» и «Солнце», предикат – отношение «вращается».
В зависимости от содержания предиката суждения, т.е. от того, что именно утверждается или отрицается о тех или иных предметах, различают атрибутивные, экзистенциальные и реляционные суждения.
Атрибутивными называются суждения, в которых утверждается или отрицается наличие некоторого свойства у предмета. Логическая форма атрибутивного суждения имеет вид: S (не) есть Р.
Пример. «Солнце (S) есть раскаленное небесное тело (Р)»; «Великобритания (S) является конституционной монархией (Р)»; «Некоторые лебеди (S) белые (Р)»; «Великий комбинатор (Р) этот Остап Бендер (S)»; «Нужда (S) заставит Богу молиться (Р)».
Экзистенциальными называются суждения, в которых утверждается или отрицается существование предмета.
Пример. «Змея-Горыныча (S) не существует в действительности (Р)»; «Природные аномалии (S) существуют (Р)»; «Нет безысходных ситуаций» («Безысходных ситуаций (S) не существует (Р)»).
Реляционные – это суждения, в которых утверждается или отрицается отношение между некоторыми предметами.
Пример. «Земля вращается вокруг Солнца»; «Петр – брат Ивана»; «Москва расположена между Петербургом и Екатеринбургом».
В атрибутивных суждениях, как и в суждениях существования, имеется всегда лишь один субъект. В суждениях об отношении – более чем один.
23.Простые суждения. Классификация простых суждений.
Простым называется суждение, выражающее связь двух понятий или выраженное одним понятием, когда второе подразумевается, лишь мыслится. Например, «Сидоров имеет высшее юридическое образование», «Ночь», «Моросит». Суждение, состоящее из нескольких простых суждений, называется сложным. Например, «Преступность и наказуемость деяния определяется уголовным законом, действовавшим во время совершения этого деяния». Это суждение состоит из двух простых: «Преступность деяния определяется уголовным законом, действовавшим во время совершения этого деяния» и «Наказуемость деяния определяется уголовным законом, действовавшим во время совершения этого деяния».
Простые суждения классифицируются по следующим основаниям.
1. По объему субъекта (по количеству):
Единичные - суждения, включающие утверждение или отрицание об одном предмете субъекта рассуждения. Их формула:
Это S есть (не есть) Р
Так, выражение «Московский гуманитарно-экономический институт готовит квалифицированных юрисконсультов» - единичное суждение, так как объем субъекта - «Московский гуманитарно-экономический институт» -включает конкретное высшее учебное заведение.
Частные - суждения, в которых что-либо утверждается или отрицается о части предметов некоторого класса. Эта часть может быть определенной и неопределенной. В зависимости от данного обстоятельства частные сужения подразделяются на определенные и неопределенные.
Определенное частное суждение содержит знание и о той, и о другой части субъекта суждения. Оно имеет такую логическую схему:
Только некоторые S есть (не есть) Р
Например, «Только некоторые правовые концепции базируются на философских принципах».
Логическая схема неопределенного суждения такова:
Некоторые S есть (не есть) Р
Квантор «некоторые» придает ему неопределенность. Например: «Некоторые проблемы юриспруденции носят философский характер».
Общие - суждения, в которых что-либо утверждается или отрицается о каждом предмете данного класса. Логические схемы таких суждений имеют вид:
Все S есть Р или Ни одно S не есть Р
Например, «Каждая страна имеет свой гимн» является общим суждением, так как объем субъекта включает весь класс отображаемых предметов.
2. По качеству связки (по качеству) суждение может быть утвердительным или отрицательным.
Утвердительное суждение выражает принадлежность предмету некоторого признака. Например, «Лицо, виновное в совершении преступления, привлекается к уголовной ответственности».
Отрицательное суждение выражает отсутствие у предмета некоторого признака. Например, «Некоторые противоправные действия не являются преступлениями».
При этом следует различать отрицательное суждение, (например, «Захватническая война не имеет законного основания») и негативную форму выражения утвердительного суждения (например, «Захватническая война незаконна»). Такого вида суждения не всегда идентичны.
3. По содержанию предиката суждение делится на суждение свойства (атрибутивное), суждение отношения (релятивное) и суждение существования (экзистенциальное).
Суждение свойства (атрибутивное суждение) отражает принадлежность или не принадлежность предмету мысли того или иного свойства, состояния. Например, «Прокурор - это человек, имеющий специальное юридическое образование».
Суждение отношения (релятивное суждение) выражает различные связи между предметами мысли по месту, времени, причиной зависимости. Например, «Благополучие государства зависит от законов» (Аристотель).
Суждение существования (экзистенциальное суждение) указывает на факт наличия или отсутствия того или иного предмета мысли. К таким суждениям относятся, например, «Нет преступления без указания о том в законе» или «Не существует абсолютной повторяемости явлений».
В классической логике различают также категорическое суждение, в котором утверждение или отрицание выражается без формулировки каких-либо условий и без каких-либо вариантов. Обычно к категорическим относят все атрибутивные суждения.
Таковы основные виды простых суждений. Любое суждение имеет количественную и качественную определенность. Поэтому в логике применяется объединенная классификация суждений по количеству и но качеству. В результате получаем четыре вида суждений: общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные. Рассмотрим их подробно.
Общеутвердительное суждение - общее по объему субъекта и утвердительное по качеству связки. Его логическая структура: «Все S есть Р», а символом служит латинская буква «А». Примером является суждение: «Все адвокаты - юристы».
Общеотрицательное суждение - общее по объему субъекта и отрицательное по качеству связки. Его логическая структура: «Ни одно S не есть Р». Символом общеотрицательных суждений служит буква «Е». Например, «Ни один подложный документ не является доказательством».
Частноутвердительное суждение - частное по объему субъекта и утвердительное по качеству связки. Его логическая структура: «Некоторые S есть Р». Символом частноутвердительных суждений служит латинская буква «I». Примерами таких суждений являются: «Некоторые студенты — юристы» или «Некоторые писатели - фронтовики».
Частноотрицательное суждение — частное по объему субъекта и отрицательное по качеству связки. Его логическая структура: «Некоторые S не есть Р», а символом служит буква «О». Примерами частноотрицательных являются следующие суждения: «Некоторые европейские страны не являются членами НАТО» или «Некоторые люди не являются юристами».
Единичные суждения в объединенной классификации приравниваются к общим суждениям, например, «Московская прокуратура проводит расследование», так как имеется в виду весь объем субъекта.
С отношениями объемов терминов в суждении связана проблема их распределенности.
Распределенным термин считается тогда, когда он взят в полном объеме. Термин считаетсянераспределенным, если он взят в части объема. Исследование распределенности терминов суждения — это не формальная логическая операция, а подтверждение правильной связи субъекта и предиката в суждении, то есть ее соответствия объективному отношению самих предметов.
24.Сложные суждения. Классификация сложных суждений.
Сложным называется суждение, в составе которого можно выделить хотя бы одно простое суждение. В зависимости от союза, с помощью которого простые суждения входят в состав сложного, выделяется, как правило, шесть видов сложных суждений. Конъюнктивное суждение или конъюнкция — это сложное суждение с соединительным союзом «и», который обозначается в логике условным знаком «/\». С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы а /\ в (читается «а и в»), где а и в — это два каких-либо простых суждения. Например, сложное суждение «Сверкнула молния, и загремел гром» является конъюнктивным или конъюнкцией (соединением) двух простых суждений. 1)Сверкнула молния. 2)Загремел гром.
Конъюнкция может состоять не только из двух, но и из большего количества простых суждений. Например: «Сверкнула молния, и загремел гром, и пошел дождь» (а /\ в /\ с). Дизъюнктивное суждение или дизъюнкция — это сложное суждение с разделительным союзом «или». Этот союз может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем). Неудивительно поэтому, что дизъюнктивные суждения делятся на два вида. Нестрогая дизъюнкция — это сложное суждение с разделительным союзом «или» в его неисключающем (нестрогом) значении, который обозначается условным знаком \/. С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы а \/ в (читается «а или в»), где а и в — это два каких-либо простых суждения. Например, сложное суждение «Он изучает английский, или он изучает немецкий» является нестрогим дизъюнктивным или нестрогой дизъюнкцией (разделением) двух простых суждений. 1)Он изучает английский. 2)Он изучает немецкий.
Как видим, эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, в силу чего данная дизъюнкция является нестрогой. Строгая дизъюнкция — это сложное суждение с разделительным союзом «или» в его исключающем (строгом) значении, который обозначается условным знаком «\/». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы а \/ в (читается «или а, или в»), где а и в — это два каких-либо простых суждения. Например, сложное суждение «Он учится в 9 классе, или он учится в 11 классе» является строгим дизъюнктивным или строгой дизъюнкцией (разделением) двух простых суждений. 1) Он учится в 9 классе. 2)Он учится в 11 классе. Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9 и в 11 классе (если он учится в 9 классе, то обязательно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой. Как нестрогая, так и строгая дизъюнкция могут состоять не только из двух, но из большего числа простых суждений. Например: «Он изучает английский или он изучает немецкий, или он изучает французский» (а \/ в \/ с) или «Он учится в 9 классе или он учится в 10 классе, или он учится в 11 классе» (а \/ в \/ с). Импликативное суждение или импликация — это сложное суждение с условным союзом «если… то», который обозначается условным знаком →.
С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы а → в (читается «если а, то в»), где а и в — это два каких-либо простых суждения. Например, сложное суждение «Если вещество является металлом, то оно электропроводно» представляет собой импликативное суждение или импликацию (причинно-следственную связь) двух простых суждений. 1)Вещество является металлом. 2) Вещество электропроводно. Как видим, в данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество — металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом).
Первая часть импликации называется основанием, а вторая — следствием. Эквивалентное суждение или эквиваленция — это сложное суждение с союзом «если… то» не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентом). В данном случае этот союз обозначается условным знаком ↔, с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы а ↔ в (читается «если а, то в, и если в, то а»), где а и в — это два каких-либо простых суждения.
Например, сложное суждение «Если число является четным, то оно делится без остатка на 2» представляет собой эквивалентное суждение или эквиваленцию (равенство, тождество) двух простых суждений. 1) Число является четным. 2) Число делится без остатка на 2. Нетрудно заметить, что в данном случае два суждения связаны так, что из первого вытекает второе, а из второго — первое: если число четное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно четное. Понятно, что в эквиваленции, в отличие от импликации, не может быть ни основания, ни следствия, т.к. две ее части являются равнозначными суждениями. Отрицательное суждение или отрицание — это сложное суждение с союзом «неверно, что…», который обозначается условным знаком. С помощью этого знака отрицательное суждение можно представить в виде формулы а (читается «неверно, что а»), где а — это какое-либо простое суждение.
25.Отношения между простыми суждениями. Логический квадрат.
Несравнимыми среди простых суждений являются суждения, имеющие различные субъекты или предикаты.
Сравнимыми являются суждения с одинаковыми субъектами и предикатами.
 Для иллюстрации отношений между простыми суждениями используется логический квадрат:
Для иллюстрации отношений между простыми суждениями используется логический квадрат:
Среди сравнимых различают совместимые суждения, которые могут быть одновременно истинными, и несовместимые суждения, которые одновременно истинными быть не могут.
Совместимость бывает трех видов: полная совместимость (эквивалентность); подчинение; частичная совместимость (субконтрарность). Несовместимость бывает двух видов: противоположность (контрарность) и противоречивость (контрадикторность).
I. Отношением подчинения связаны суждения А и I, Е и О. Общие суждения (А и Е) являются подчиняющими, а частные (I, О) подчиненными. Для суждений находящихся в отношении подчинения, имеет значение условие истинности: Если истинно А(Е), то истинно и I(O), но не наоборот.
II. Отношением противоречия связаны суждения Е и I, А и О. Два противоречивых суждения (согласно законам логики) не могут быть одновременно ни истинными, ни ложными Если А - истинно, то О - ложно
Если А - ложно, то О - истинно
Если О - истинно, то А - ложно
Если О - ложно, то А - истинно
Если Е - истинно, то I - ложно
Если Е - ложно, то I - истинно
Если I -истинно, то E - ложно
Если I - ложно, то E - истинно
III. Отношением контрарности (противоположности) связаны только общие суждение А и Е. Закон исключения третьего к таким суждениям не применим. А и Е могут оказаться одновременно ложными, но не могут быть одновременно истинными (пример: оба суждения " Все любят логику" и " никто не любит логику" - ложны).
IV. Отношение субконтрарности существует между частными суждениями I и О. I и О могут быть одновременно истинными, но не могут быть одновременно ложными (пример: оба суждения " Некоторые люди любят логику" и " некоторые люди не любят логику" - истинны).
26.Отношения между сложными суждениями.
Сопоставление сложных суждений позволяет разделить их на группу независимых и группу зависимых суждений.
К независимым относятся суждения, которые не имеют общих составляющих; для них характерны все сочетания истинных значений. Зависимые - это суждения, которые имеют одинаковые составляющие и могут различаться логическими связками, включая отрицание. Пример зависимых сложных суждений: " Норвегия или Швеция имеют выход к Балтийскому морю" и " Не верно, что Норвегия и Швеция имеют выход к Балтийскому морю". Хотя эти суждения различны по логической форме (первое из них - дизъюнктивное суждение, а второе - отрицание конъюнкции), вместе с тем они зависимы, поскольку включают одинаковые составляющие.
Сложные зависимые суждения могут быть совместимыми и несовместимыми.
Отношение совместимости.
К совместимым относятся суждения, которые одновременно могут быть истинными. Как и в случае простых суждений различают три вида совместимости сложных суждений: эквивалентность, частичная совместимость и подчинение.
Эквивалентными являются такие суждения, которые принимают одни и те же значения, т. е. одновременно являются либо истинными, либо ложными.
Отношение эквивалентности позволяет выражать одни сложные суждения через другие - конъюнкцию через дизъюнкцию или импликацию, и наоборот.
Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.
Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего, подчиненное всегда будет истинным.
Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующего все виды рассуждений.
Отношение несовместимости.
Несовместимыми являются суждения, которые одновременно не могут быть истинными. Из двух видов несовместимости одна - противоположность, другая - противоречие.
Противоположность - отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными.
Противоречащими являются суждения, которые одновременно не могут быть ни истинными, ни ложными. При истинности одного из них другое будет ложным, а при ложности первого второе будет истинным.
Чтобы получить сложное суждение, противоречащее исходному, последнее нужно подвергнуть отрицанию.
Сопоставление суждений в дискуссиях. Отчетливое представление об отношениях, в которых могут находиться суждения, позволяет логически грамотно анализировать высказывания участников дискуссий. Встречаются ситуации, когда логический анализ показывает совместимость различных по структуре суждений. Нередко это случается с частными суждениями. Пропонент утверждает, что " Некоторые S есть Р"; оппонент настаивает, что " Некоторые S не есть Р". На поверку же выходит, что эти суждения не исключают друг друга, а являются частично совместимыми и оба могут оказаться истинными.
В спорах и дискуссиях могут смешиваться противоречащие и противоположные суждения; Например, обвинитель утверждает, что в рассматриваемом случае имело место убийство, которое совершено умышленно. Защитник не отрицает факта убийства, но считает, что оно было совершено без умысла. Каждый из них считает, что утверждения исключают друг друга как альтернативные. В действительности же оказывается, что эти высказывания находятся в отношении противоположности. Отсюда следует, что если будет показана в целом несостоятельность утверждения обвинителя, то это еще не означает правоту защитника. Точно так же опровержение утверждений защитника логически не обязывает принимать точку зрения обвинителя. Может оказаться, что оба утверждения ложны, и задача сведется к поиску нового объяснения фактам.
27.Правила построения таблицы истинности.
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2n, где n - количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Пример 1. Для формулы A/\ (B \/ B /\C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк - 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов - 3 + 5 = 8.

Пример 2. Определите истинность логического выражения F(А, В) = (А\/ В)/\(А\/В).
1. В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) А; 3) В; 4) А\/В; 5) (А\/ В)/\(А\/В).
5. Кстолбцов=n+5=2+5=7 столбцов.
| А | В | А\/ В | А | В | А\/В | F |
Вывод: логическое выражение принимает значение истина при наборахF(0, 1)=1 и F(1, 0)=1.
28.Умозаключение. Структура умозаключений.
Познавая окружающую действительность, мы приобретаем новые знания. Некоторые из них – непосредственно, при помощи чувств; другие же — опосредованно, на основании логического мышления, путем выведения новых знаний из знаний уже имеющихся. Эти знания называются опосредствованными, или выводными. Логической формой получения выводных знаний является умозаключение.
Умозаключение — это форма мышления, посредством которой из одного или нескольких суждений выводится новое суждение. Логическая сущность умозаключения состоит в движении мысли от анализа имеющегося знания к синтезу нового знания. Это движение имеет объективный характер и определяется реальными связями действительности. Объективная связь, отраженная в сознании, обеспечивает логическую связь мыслей. Напротив, отсутствие объективных связей действительности приводит к логическим ошибкам.
Структура любого умозаключения включает 3 элемента [3, c.157]:
· посылки - исходное знание (суждение), из которого выводится новое суждение;
· обосновывающее знание, выражающееся в правилах или выводе умозаключения (логический переход от посылок к заключению);
· выводное знание, выражающееся в заключении или выводе (новое суждение, полученное логическим путем из посылок).
При анализе умозаключения посылки и заключение принято записывать отдельно, располагая их друг над другом. Заключение записывают под горизонтальной чертой, отделяющей его от посылок и обозначающей логическое следование. В соответствии с этим рассмотрим следующий пример умозаключения:
Все граждане России имеют право на образование – посылка
Новиков – гражданин России - посылка
Новиков имеет право на образование – заключение
При наличии содержательной связи между посылками можно получить в процессе рассуждения новое истинное знание при соблюдении двух условий.
Во-первых, должны быть истинными исходные суждения – посылки. Однако следует сказать, что иногда и ложные суждения могут дать истинное заключение. Так, в результате специального подбора ложных посылок в следующем рассуждении получим истинное заключение: Все слоны имеют крылья. Все птицы – слоны. Все птицы имеют крылья.
Это свидетельствует о том, что ориентация только на форму (структуру) посылок при игнорировании их объективно – истинных связей может создать видимость правильного умозаключения.
Во-вторых, в процессе рассуждения необходимо соблюдать правила вывода, которые обусловливают логическую правильность умозаключения. Без этого даже из истинных посылок можно получить ложное заключение. Например: Все гусеницы едят капусту. Я ем капусту. Следовательно, я гусеница.
29.Умозаключение. Классификация умозаключений.
Умозаключение -- это способ получения нового знания на основе некоторого имеющегося.
Он представляет собой переход от некоторых высказываний, фиксирующих наличие некоторых ситуаций в действительности, к новому высказыванию и соответственно к знанию о наличии ситуации, которую описывает это высказывание. Например, в механике известно, что у всякого тела, плотность которого одинакова во всех его частях, геометрический центр и центр тяжести совпадают. Известно также (в результате астрономических наблюдений), что у Земли эти центры не совпадают. Отсюда естественно заключить, что плотность Земли не является одинаковой во всех ее частях. Едва ли нужно специально говорить о значении этой операции в познавательной и практической деятельности. Посредством умозаключений мы получаем приращение знаний, не обращаясь к исследованию предметов и явлений самой действительности, имеем возможность открывать такие связи и отношения действительности, которые невозможно усмотреть непосредственно.
Классификация умозаключений
По степени общности посылок и вывода умозаключения делятся на три группы:
a. дедуктивные, когда мысль идет от большей к меньшей общности знания;
b. индуктивные, когда мысль развивается от знания одной степени общности к новому знанию большей степени общности;
c. по аналогии, когда посылки и вывод выражают знание одинаковой степени общности.
30.Непосредственные умозаключения.
Непосредственными называют умозаключения из одной посылки, представляющей собой простое суждение.
Превращение состоит в том, что мы в нашу посылку вставляем два отрицания – одно перед связкой, а другое – перед предикатом, и так получаем новое суждение. Умозаключения принято изображать так: сначала пишется посылка (или посылки), под ней проводится черта, обозначающая слово «следовательно», а под чертой пишется вывод. Пусть посылкой у нас будет общеутвердительное суждение, тогда превращение выглядит так:
Все S есть P
Ни одно S не есть не-P
Например, суждение «Все металлы электропроводны» превращается в суждение «Ни один металл не
является неэлектропроводным».
Если в качестве посылки взять общеотрицательное суждение, то превращение будет выглядеть так:
Ни одно S не есть P
Bce S есть не-P
Например, суждение «Ни один мошенник не является честным человеком» превращается в суждение «Все мошенники являются нечестными людьми». Когда здесь мы вставляем «не» перед связкой, то перед ней получаются два «не». Мы устраняем их, опираясь на принцип: двойное отрицание эквивалентно утверждению.
Конечно, вывод в таких умозаключениях дает очень мало нового по сравнению с посылкой. Это вполне естественно, так как мы по сути дела одному и тому же суждению лишь придаем иную языковую форму. Это не столько логическая, сколько грамматическая игра. Однако преобразование такого рода способно сделать явными некоторые оттенки смысла первоначального суждения, которые были скрыты в исходной формулировке. Мы часто пользуемся превращением суждений в повседневной жизни, когда хотим более ясно и отчетливо выразить свою мысль. Это часть нашей языковой способности.
Еще одной разновидностью непосредственного умозаключения является обращение. При обращении вывод получается путем постановки предиката посылки на место субъекта, а субъекта посылки – на место предиката. Общая схема обращения выглядит следующим образом:
S есть P
P есть S
Например, из суждения «Птицы есть позвоночные» мы путем обращения получаем вывод «Позвоночные есть птицы». Для того чтобы реально осуществить обращение, мы должны не просто поменять местами субъект и предикат, а сделать объект, отображаемый предикатом посылки, предметом нашей мысли, т.е. превратить его в субъект нового суждения. Иногда, например, производят обращение так: из суждения «Все рыбы дышат жабрами» получают вывод «Дышат жабрами все рыбы». Здесь нет логической операции обращения! Мы просто поменяли местами подлежащее и сказуемое. Чтобы получить обращение первоначального суждения, мы должны сделать предметом нашей мысли «дышащих жабрами» и говорить о них: «Дышащие жабрами есть рыбы».
В посылке перед субъектом стоит слово (квантор): «все» или «некоторые». Возникает вопрос: что мы должны поставить перед предикатом посылки, когда делаем его субъектом вывода, – «все» или «некоторые»? «Все дышащие жабрами» или только «некоторые дышащие жабрами» есть рыбы? Пытаясь ответить на этот вопрос, мы начинаем вдумываться в содержание понятия «дышащие жабрами», вспоминаем, а кто еще, помимо рыб, мог бы дышать жабрами, быть может, лягушки или какие-нибудь тритоны? Не нужно всего этого! Логика – наука формальная и вовсе не обязана знать, чем занимаются лягушки или рыбы, как математика, складывая 2 и 3, вовсе не интересуется тем, что вы считаете – рубли, доллары или кирпичи. Логика задает формальные правила, не зависящие от содержания наших понятий и суждений. В данном случае правило таково: если посылкой является утвердительное суждение, то при обращении перед предикатом ставят слово «некоторые»; если же посылка является отрицательным суждением, то перед предикатом ставят слово «все». Наша посылка «Все рыбы дышат жабрами» является утвердительным суждением, значит, из нее можно сделать вывод «Некоторые дышащие жабрами есть рыбы». А вот из отрицательной посылки «Ни один слон не живет в Арктике» можно сделать общий вывод «Всякий живущий в Арктике не есть слон».
2) Три путешественника забрели на постоялый двор, хорошо покушали, заплатили хозяйке 30 руб. и пошли дальше. Через некоторое время после их ухода хозяйка обнаружила, что взяла с путешественников лишнее. Будучи женщиной честной, она оставила себе 25 руб., а 5 руб. дала мальчику, наказав ему догнать путешественников и отдать им эти деньги. Мальчик бегал быстро и скоро догнал путешественников. Как им разделить 5 руб. на троих? Каждый из них взял по 1 руб., а 2 руб. оставили мальчику в награду за быстроногость.
Таким образом, они заплатили за обед по 10руб., но по 1 руб. получили обратно, следовательно, они заплатили: 9х3 = 27руб. Да 2 руб. осталось у мальчика: 27 + 2 = 29 руб. Но вначале-то было 30 руб.! Куда делся 1 руб.?
3) Жили-были два пастуха, Иван да Петр, пасли они овец. И вот как-то Иван говорит: «Слушай, отдай мне одну овцу, тогда у меня овец будет в 3 раза больше, чем у тебя!». «Нет, – отвечает Петр, – лучше ты мне отдай одну овцу, тогда у нас их станет поровну!»
Сколько овец было у Ивана и сколько у Петра?
31. Непосредственно умозаключения. Обращение.
Отв. Непосредственные умозаключения - такие, в которых заключение выводится из одной посылки. Например, из суждения «Все адвокаты - юристы» можно получить новое суждение «Некоторые юристы - адвокаты». Непосредственные умозаключения дают нам возможность выявить знание о таких сторонах предметов, которое уже содержалось в исходном суждении, но не было явно выражено и явно осознано. В этих условиях мы делаем неявное - явным, неосознанное - осознанным.
К непосредственным умозаключениям относятся: превращение, обращение, противопоставление предикату, умозаключение по «логическому квадрату».
Обращение - такое непосредственное умозаключение, в котором происходит перемена мест субъекта и предиката при сохранении качества суждения.
Обращение подчиняется правилу распределенности терминов: если термин не распределен в посылке, то он не должен быть не распределен и в заключении.
Если обращение ведет к изменению исходного суждения по количеству (из общего исходного получается новое частное суждение), то такое обращение называется обращением с ограничением; если обращение не ведет к изменению исходного суждения по количеству, то такое обращение является обращением без ограничения.
Примеры и схемы обращения:
А: Общеутвердительное суждение обращается в частноутвердительное.
Все адвокаты - юристы.
Некоторые юристы - адвокаты.
Все S суть Р.
Некоторые Р суть S.
Общеутвердительные выделяющие суждения обращаются без ограничения. Всякое правонарушение (и только правонарушение) суть противоправное деяние.
Всякое противоправное деяние суть правонарушение.
Схема:
Все S, и только S, суть Р.
Все Р суть S.
Е: Общеотрицательное суждение обращается в общеотрицательное (без ограничения).
Ни один адвокат не судья.
Ни один судья не адвокат.
Ни один S не есть Р.
Ни один Р не есть S.
I: Частноутвердительные суждения обращаются в частноутвердительные.
Некоторые юристы - спортсмены.
Некоторые спортсмены - юристы.
Некоторые S суть Р.
Некоторые Р суть S.
Частноутвердительные выделяющие суждения обращаются в общеутвердительные:
Некоторые юристы, и только юристы, являются адвокатами.
Все адвокаты суть юристы.
Некоторые S, и только S, суть Р.
Все Р суть S.
О: Частноотрицательные суждения не обращаются.
Логическая операция обращения суждения имеет большое практическое значение. Незнание правил обращения приводит к грубым логическим ошибкам. Так, довольно часто общеутвердительное суждение обращается без ограничения. Например, суждение «Все юристы должны знать логику» обращается в суждение «Все изучающие логику - юристы». Но это неверно. Верно суждение «Некоторые изучающие логику – юристы».
32. Непосредственные умозаключения. Противопоставление предикату.
Отв. Непосредственные умозаключения - такие, в которых заключение выводится из одной посылки. Например, из суждения «Все адвокаты - юристы» можно получить новое суждение «Некоторые юристы - адвокаты». Непосредственные умозаключения дают нам возможность выявить знание о таких сторонах предметов, которое уже содержалось в исходном суждении, но не было явно выражено и явно осознано. В этих условиях мы делаем неявное - явным, неосознанное - осознанным.
Противопоставление предикату - это последовательное применение операций превращения и обращения - преобразование суждения в новое суждение, в котором субъектом становится понятие, противоречащее предикату, а предикатом - субъект исходного суждения; меняется качество суждения.
Например, из суждения «Все адвокаты - юристы» можно, противопоставляя предикат, получить «Ни один не-юрист не является адвокатом». Схематически:
Все S суть Р.
Ни одно не- Р не есть S.
33. Простой категорический силлогизм.
Отв. Простой категорический силлогизм (простое дедуктивное умозаключение) - такое умозаключение, в котором заключение и посылки являются простыми категорическими суждениями. Категорические суждения - такие, в которых мысль утверждается или отрицается вполне определенно, без всяких условий, и которые имеют субъектно-предикатную структуру.
Пример:
Все адвокаты - юристы.
Петров - адвокат.
Петров - юрист.
Проанализируем структуру силлогизма. Понятия, входящие в состав силлогизма, называются терминами силлогизма. Различают меньший, больший и средний термины.Меньший термин - понятие, которое в заключении является субъектом (в нашем примере - понятие «Петров») и обозначается буквой «S». Больший термин - понятие, которое в заключении является предикатом («юрист») и обозначается «Р». Средний термин -понятие, которое входит в обе посылки и не входит в заключение («адвокат»), обозначается буквой «М» (от лат. medium - средний). Схема силлогизма:
Все М есть Р.
S есть М.
S есть Р.
Каждая из посылок имеет свое название: та посылка, в которую входит больший термин, называется большей посылкой. Та, в которую входит меньший термин, называется меньшей посылкой. В посылках дано отношение меньшего и большего терминов к среднему термину. В заключении устанавливается отношение между меньшим и большим терминами.
Последовательность посылок и заключения в естественном языке может быть различной. Но в процессе логического анализа силлогизма посылки принято располагать в определенной последовательности: большую посылку - на первом месте, меньшую - на втором.
Отношения между терминами в вышеуказанном силлогизме можно изобразить в круговых схемах:
В основе вывода по категорическому силлогизму лежит аксиома силлогизма: «Все, что утверждается (или отрицается) относительно всех предметов класса, утверждается (или отрицается) относительно каждого предмета (или любой части предметов) этого класса».
Силлогизмы могут быть правильно построенные и неправильно построенные. Рассмотрим общие правила силлогизма (три правила терминов и четыре правила посылок).
Правила терминов:
1. В силлогизме должно быть только три термина. Нарушение этого правила связано с отождествлением разных понятий, которые принимаются за одно и рассматриваются как один термин. Ошибка: «учетверение терминов».
Мышь грызет книжку.
Мышь - имя существительное.
Имя существительное грызет книжку.
Ошибка связана с тем, что слово «мышь» выражает различные понятия (имеет разный смысл).
2. Средний термин должен быть распределен хотя бы в одной из посылок. Если средний термин не распределен ни в одной из посылок, то связь между крайними терминами остается неопределенной.
Некоторые растения (М-) ядовиты (Р).
Белые грибы (S) - растения (М-).
Белые грибы (S) - ядовиты (Р).
Средний термин не распределен ни в одной из посылок. Поэтому необходимую связь между терминами нельзя установить.
3. Термин, не распределенный в посылке, не может быть распределен в заключении.Ошибка: «незаконное распределение меньшего (или большего) термина».
Во всех городах за полярным кругом (М) бывают белые ночи (Р-).
Санкт-Петербург (S) не находится за Полярным кругом (М).
В Санкт-Петербурге (S) не бывает белых ночей (Р+).
Заключение ложное, так как нарушено данное правило. Предикат (Р) в посылке не распределен, а в заключении - распределен. Следовательно, произошло расширение большего термина.
Правила посылок:
1. Хотя бы одна из посылок должна быть утвердительным суждением.
Адвокаты не судьи.
Студенты не адвокаты.
?
2. Если одна из посылок - отрицательное суждение, то и заключение - отрицательное суждение.
Все адвокаты юристы.
Петров не юрист.
Петров не адвокат.
3. Хотя бы одна из посылок должна быть общим суждением.
Некоторые юристы спортсмены.
Некоторые юристы любят музыку.
?
4. Если одна из посылок частная, то и заключение должно быть частным.
Все преступники должны быть наказаны.
Некоторые люди - преступники.
Некоторые люди должны быть наказаны.
34. Фигуры и модусы категорического силлогизма.
Отв.
Фигуры и правила фигур силлогизма. В зависимости от места среднего термина в посылках различают четыре фигуры категорического силлогизма.
Первая фигура - разновидность силлогизма, в которой средний термин занимает место субъекта в большей посылке (М - Р) и место предиката в меньшей посылке (S - М).Например:
Все адвокаты (М) - юристы (Р)
Петров (S) - адвокат (М).
Петров (S) - юрист (Р).
М-Р - большая посылка.
S - М - меньшая посылка.
S — Р - заключение.
Правила первой фигуры:
Ø большая посылка должна быть общим суждением (А, Е);
Ø меньшая посылка должна быть утвердительным суждением (А, I).
Первая фигура силлогизма широко применяется в юридической науке и практике. Так, по первой фигуре производится квалификация различных правовых явлений, преступлений, фактов судебной практики. При этом большей посылкой выступает та или иная статья кодекса, правовая норма, закон, а меньшей - рассматриваемый конкретный случай. В заключении делается вывод о рассматриваемом случае на основании общего положения. Например, «Тайное хищение чужого имущества составляет кражу. Данный человек совершил тайное хищение чужого имущества. Следовательно, данный человек совершил кражу».
Вторая фигура - разновидность простого силлогизма, в которой средний термин занимает место предиката в обеих посылках.
Например:
Все адвокаты (М) - юристы.
Петров - не юрист (М).
Петров - не адвокат.
Р - М - большая посылка.
S - М - меньшая посылка.
S — Р - заключение.
Правила второй фигуры:
Ø большая посылка должна быть общим суждением (А, Е);
Ø одна из посылок должна быть отрицательной (Е, О).
Вторая фигура применяется при доказательствах ложности какого-либо положения путем отрицания принадлежности исследуемых предметов к классу предметов, о которых мыслится в большей посылке. В судебной практике данная фигура служит для логического обоснования отсутствия состава преступления в том или ином конкретном деянии, для доказательства неправильной квалификации преступления, для опровержения каких-либо положений, не согласующихся с общим правилом. Например, «Этот смертельный удар нанесен человеком, обладающим огромной физической силой. Обвиняемый не является человеком, обладающим огромной физической силой. Следовательно, обвиняемый не мог нанести этот смертельный удар».
Третья фигура - разновидность силлогизма, в которой средний термин занимает место субъекта в обеих посылках (М - Р; М - S). Например:
Все подозреваемые (М) признали свою вину.
Все подозреваемые (М) привлечены к уголовной ответственности.
Некоторые привлеченные к уголовной ответственности, признали свою вину.
М - Р - большая посылка.
М - S - меньшая посылка.
S - Р - заключение.
Правила третьей фигуры:
Ø меньшая посылка должна быть утвердительным суждением (А, I);
Ø о заключение должно быть частным суждением (I, О).
Третья фигура служит чаще всего для установления частичной совместимости признаков, относящихся к одному и тому же предмету. Она также может быть применима для опровержения отдельных общих положений. Например, необходимо опровергнуть суждение «Ни один свидетель не дал правдивых показаний» (т. е. доказать противоречащее ему суждение «Некоторые свидетели дали правдивые показания») и известно, что свидетели X. и Y. дали правдивые показания. Построим умозаключение по третьей фигуре:
X. и Y. (М) - дали правдивые показания.
X. и Y. (M) - свидетели.
Некоторые свидетели дали правдивые показания.
P - M- большая посылка.
S - M - меньшая посылка.
S-P- заключение.
Поскольку частноутвердительное суждение «Некоторые свидетели дали правдивые показания» является истинным, то находящееся с ним в отношении противоречия общеотрицательное суждение «Ни один свидетель не дал правдивых показаний» - ложное.
Четвертая фигура - разновидность силлогизма, в которой средний термин занимает место предиката в большей и место субъекта в меньшей посылке (Р - M, M - S), схематично выражается:
Р - М - большая посылка.
М - S - меньшая посылка.
S - Р - заключение.
Четвертая фигура силлогизма практически не употребляется.
По первой фигуре можно получить выводы из всех основных видов суждений. Вторая фигура дает только отрицательный вывод. В третьей фигуре вывод будет частным суждением.
В зависимости от того, какие суждения по количеству и качеству составляют простой категорический силлогизм (являются посылками и заключением), различают виды силлогизмов, которые называют модусами. Модусы простого категорического силлогизма - это его разновидности, отличающиеся друг от друга качественной и количественной характеристикой входящих в них посылок и заключения.
В четырех фигурах силлогизма максимальное число комбинаций равно 64. Однако правильных модусов всего 19:
Первая фигура: ААА, ЕАЕ, АII, ЕIО
Вторая фигура: ЕАЕ, АЕЕ, ЕIО, АОО
Третья фигура: AAI, IAI, АII, ЕАО, ОАО, ЕIО
Четвертая фигура: AAI, АЕЕ, IAI, ЕАО, ЕIО
В соответствии с этим называют модусы первой фигуры, модусы второй фигуры и т. д. Например, модус ААА 1-й фигуры, модус АЕЕ 2-й фигуры и т.д. Все другие модусы возможны, но они являются неправильными, так как в них нарушаются те или иные правила категорического силлогизма. Знание модусов дает возможность определить форму истинного заключения, когда даны посылки и известно, какова фигура данного силлогизма.
Знания специальных правил фигур являются производными от перечисленных выше общих правил силлогизма. Главная трудность при проверки правильности того или иного силлогизма состоит в том, чтобы правильно построить умозаключение. Правила простого категорического силлогизма не позволяют определить содержание посылок, но они указывают, каким требованиям эти посылки должны удовлетворять, чтобы их можно было связать между собой и сделать необходимое заключение.
Но умозаключения строятся не только из простых, но и из сложных суждений. Широко используются умозаключения, посылками которых являются условные и разделительные суждения, выступающие в разных сочетаниях друг с другом или с категорическими суждениями
35. Умозаключения из сложных суждений. Классификация сложных умозаключений.
Отв. Умозаключения из сложных суждений представляют интерес, поскольку в них выводы зависят только от логических связей между суждениями, а не от их субъектно-предикатной структуры.
В современной логике существует несколько универсальных способов решения вопроса о правильности любого дедуктивного умозаключения из сложных суждений (с помощью таблиц истинности, методом аналитических таблиц, средствами натурального исчисления высказываний). Но наиболее часто встречающиеся формы умозаключений целесообразно просто запомнить, чтобы только по логической структуре определять их правильность.
Разделительно-категорическое умозаключение.
В данном виде дедуктивных умозаключений одна посылка - разделительное суждение, а вторая и вывод - категорические. Причем в категорическую посылку входит одна из альтернатив (или все, кроме одной) разделительного суждения.
Разделительно-категорическое умозаключение имеет два модуса:
1) утверждающе-отрицательный;
2) отрицательно-утверждающий.
Формула утверждающе-отрицательного модуса:
А есть или В, или С;
А есть В;
Следовательно, А не есть С.
Формула отрицающе-утверждающего модуса:
А есть или В, или С;
А не есть В;
Следовательно, А есть С.
Условно-категорическое умозаключение.
Условно-категорическое умозаключение состоит из двух посылок - условного и категорического суждений. При этом категорическая посылка состоит из тех же терминов, что основание или следствие условной посылки.
Условно-категорическое умозаключение имеет два модуса - утвердительный и отрицательный.
В утверждающем заключение идет от утверждения основания к утверждению следствия. Формула:
Если есть А, то есть В;
А есть;
Следовательно, есть В.
Вывод по этому модусу может быть и утвердительный, и отрицательный.
В отрицающем модусе заключение идет от отрицания следствия к отрицанию основания. Формула:
Если есть А, то есть В;
В нет;
Следовательно, нет А.
Вывод по этому модусу бывает утвердительный и отрицательный; его качественная сторона находится в обратной зависимости от качественного характера условной посылки.
Условно-разделительное умозаключение.
Умозаключение, в котором одна посылка - условное суждение, а другая - разделительное, называется условно-разделительным или лемматическим умозаключением. По количеству следствий условной посылки различают дилеммы, трилеммы и полилеммы.
Дилемма - это условно-разделительный силлогизм с двумя альтернативами, ибо третьего решения вопроса не существует. В практике рассуждений встречаются два вида дилемм - конструктивная и деструктивная.
В конструктивной (созидающей) дилемме из двух оснований вытекают два следствия. Вторая посылка ограничивает возможность выбора только этими двумя основаниями (альтернативами). Заключение признает оба вытекающих следствия. Таким образом, в конструктивной дилемме заключение идет от утверждения оснований к утверждению следствий. Общая схема конструктивной дилеммы:
Если А есть В, то А есть К;
если А есть С, то А есть М;
А есть либо В, либо С;
Следовательно, А есть либо К, либо М.
Пример: Если политические теории прогрессивны, то они способствуют развитию общества; Если же политические теории реакционны, то они препятствуют развитию общества.Но политические теории могут быть либо прогрессивными, либо реакционными.Политические теории либо способствуют развитию общества, либо препятствуют ему.
В деструктивной (разрушающей) дилемме из одного основания вытекают два следствия: вторая посылка отрицает оба следствия, а вывод разрушает само основание. Следовательно, в деструктивной дилемме заключение идет от отрицания следствий к отрицанию оснований. Общая схема деструктивной дилеммы:
Если А есть В, то А есть либо С, либо Д;
А не есть ни С, ни Д;
Следовательно, В не есть В.
Пример: Если философ признает первичность материи по отношению к сознанию, то он является материалистом.Если же философ признает первичность сознания по отношению к материи, то он является идеалистом.Но философ либо не является материалистом, либо не является идеалистом.Философ не признает либо первичность материи по отношению к сознанию, либо первичность сознания по отношению к материи.
При определении правомерности выводов лемматических силлогизмов нужно руководствоваться следующим: вывод правомерен, если ход рассуждений направлен от утверждения оснований к утверждению следствий или от отрицания следствий к отрицанию оснований, и неправомерен, если ход рассуждений направлен обратно указанному.
Вывод:
Один из видов умозаключения - дедуктивное умозаключение. Формой ДУ является простой категорический силлогизм, имеющий свои фигуры, модусы, правила.
36. Чисто условные умозаключения.
Чисто условным называется умозаключение, обе посылки которого являются условными суждениями. Напр.:
Если изобретение создано совместным творческим трудом нескольких граждан (р), все они признаются соавторами изобретения (q). Если они признаются соавторами изобретения (r), то порядок пользования правами на изобретение, созданное в соавторстве, определяется соглашением между соавторами (r). Если изобретение создано совместным творческим трудом нескольких граждан (р), то порядок пользования правами на изобретение, созданное в соавторстве, определяется соглашением между соавторами (r).
В приведенном примере обе посылки – условные суждения, причем следствие первой посылки является основанием второй (q), из которого, в свою очередь, вытекает некоторое следствие (r). Общая часть двух посылок (q) позволяет связать основание первой (р) и следствие второй (r). Поэтому заключение также выражается в форме условного суждения.
Схема чисто условного умозаключения:
(p > q)? (q > r),
(Р > r).
Вывод в чисто условном умозаключении основывается на правиле: следствие следствия есть следствие основания.
Умозаключение, в котором заключение получается из двух условных посылок, относится к простым.
Однако заключение может следовать из большего числа посылок, которые образуют цепь условных суждений. Такие умозаключения называются сложными.
37. Условно-категорические умозаключения.
Условно-категорическим называется умозаключение, в котором одна из посылок– условное, а другая посылка и заключение – категорические суждения.
Это умозаключение имеет два правильных модуса: утверждающий и отрицающий.
1. В утверждающем модусе (modus ponens) посылка, выраженная категорическим суждением, утверждает истинность основания условной посылки, а заключение утверждает истинность следствия; рассуждение направлено от утверждения истинности основания к утверждению истинности следствия. Напр.:
Если иск предъявлен недееспособным лицом (р), то суд оставляет иск без рассмотрения(q).
Иск предъявлен недееспособным лицом (р). Суд оставляет иск без рассмотрения (q).
Первая посылка – условное суждение, выражающее связь основания (р) и следствия (q).Вторая посылка – категорическое суждение, в котором утверждается истинность основания (р): иск предъявлен недееспособным лицом. Признав истинность основания(р), мы признаем истинность следствия (q): суд оставляет иск без рассмотрения.
Утверждающий модус дает достоверные выводы. Он имеет схему:

2. В отрицающем модусе (modus tollens) посылка, выраженная категорическим суждением, отрицает
истинность следствия условной посылки, а заключение отрицает истинность основания. Рассуждение направлено от отрицания истинности следствия к отрицанию истинности основания. Напр.: Если иск предъявлен недееспособным лицом (р), то суд оставляет иск без рассмотрения (q). Суд не оставил иск без рассмотрения (? q). Неверно, что иск предъявлен недееспособным лицом (? р). Схема отрицающего модуса:
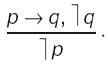
Нетрудно установить, что возможны еще две разновидности условно-категорического силлогизма: от отрицания истинности основания к отрицанию истинности следствия и от утверждения истинности следствия к утверждению истинности основания.
Однако заключение по этим модусам не будет достоверным. Таким образом, из четырех модусов условно-категорического умозаключения, исчерпывающих все возможные комбинации посылок, достоверные заключения дают два: утверждающий и отрицающий. Они выражают законы логики и называются правильными модусами условно-категорического умозаключения. Эти модусы подчиняются правилу: утверждение основания ведет к утверждению следствия и отрицание следствия – к отрицанию основания. Два других модуса достоверных заключений не дают. Они называются неправильными модусами и подчиняются правилу: отрицание основания не ведет с необходимостью к отрицанию следствия и утверждение следствия не ведет с необходимостью к утверждению основания.
38. Условно-разделительные умозаключения. Простая конструктивная диллема.
Умозаключение, в котором одна посылка - условное суждение, а другая - разделительное, называется условно-разделительным или лемматическим умозаключением. По количеству следствий условной посылки различаютдилеммы, трилеммы и полилеммы.
Дилемма - это условно-разделительный силлогизм с двумя альтернативами, ибо третьего решения вопроса не существует. В практике рассуждений встречаются два вида дилемм - конструктивная и деструктивная.
В конструктивной (созидающей) дилемме из двух оснований вытекают два следствия. Вторая посылка ограничивает возможность выбора только этими двумя основаниями (альтернативами). Заключение признает оба вытекающих следствия. Таким образом, в конструктивной дилемме заключение идет от утверждения оснований к утверждению следствий. Общая схема конструктивной дилеммы:
Если А есть В, то А есть К;
если А есть С, то А есть М;
А есть либо В, либо С;
Следовательно, А есть либо К, либо М.
Пример: Если политические теории прогрессивны, то они способствуют развитию общества; Если же политические теории реакционны, то они препятствуют развитию общества. Но политические теории могут быть либо прогрессивными, либо реакционными. Политические теории либо способствуют развитию общества, либо препятствуют ему.
В деструктивной (разрушающей) дилемме из одного основания вытекают два следствия: вторая посылка отрицает оба следствия, а вывод разрушает само основание. Следовательно, в деструктивной дилемме заключение идет от отрицания следствий к отрицанию оснований. Общая схема деструктивной дилеммы:
Если А есть В, то А есть либо С, либо Д;
А не есть ни С, ни Д;
Следовательно, В не есть В.
Пример: Если философ признает первичность материи по отношению к сознанию, то он является материалистом. Если же философ признает первичность сознания по отношению к материи, то он является идеалистом. Но философ либо не является материалистом, либо не является идеалистом. Философ не признает либо первичность материи по отношению к сознанию, либо первичность сознания по отношению к материи.
При определении правомерности выводов лемматических силлогизмов нужно руководствоваться следующим: вывод правомерен, если ход рассуждений направлен от утверждения оснований к утверждению следствий или от отрицания следствий к отрицанию оснований, и неправомерен, если ход рассуждений направлен обратно указанному.
39. Условно-разделительные умозаключения. Сложная конструктивная диллема.
В сложной деструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка отрицает оба следствия, заключение отрицает оба основания. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности оснований.
Схема сложной деструктивной дилеммы:
(p-»q)A(r-> s), 1qv1s
1р v 1r
Пример:
Если предприятие является арендным (р), то оно осуществляет предпринимательскую деятельность на основе взятого им в аренду имущественного комплекса (q); если оно является коллективным (г), то осуществляет такую деятельность на основе находящегося в его собственности имущества (s)
Данное предприятие не осуществляет свою деятельность ни на основе взятого в аренду имущественного комплекса (не-q), ни на основе находящегося в его собственности имущества (не-s)
Данное предприятие не арендное (не-р) или не коллективное (не-г)
40. Условно-разделительные умозаключения. Простая деструктивная диллема.
В простой деструктивной дилемме условная посылка содержит | одно основание, из которого вытекает два возможных следствия.
: Д Разделительная посылка отрицает оба следствия, заключение отри-;
цает основание. Рассуждение направлено от отрицания истинности;
следствий к отрицанию истинности основания.
Схема простой деструктивной дилеммы:
Пример:
(р-»д)л(р-> г), 1ду1г IP
Если Н. совершил умышленное преступление (р), значит, в его действиях был прямой (q) или косвенный умысел (г). Но в действиях Н. не было ни прямого (q), ни косвенного умысла (г).
Преступление, совершенное Н., не является умышленным (р)
41.Условно-разделительные умозаключения. Сложная деструктивная дилемма
Условно-разделительное умозаключение – это такое дедуктивное умозаключение, в котором одна посылка состоит из двух или большего количества условных суждений, а другая является разделительным суждением.
В зависимости от числа членов в разделительной посылке это умозаключение может быть дилеммой (два члена в разделительной посылке), трилеммой (три члена) и полилеммой.
Дилемма – это условно-разделительное умозаключение, в котором одна посылка состоит из двух условных суждений, а другая является разделительным