Основные способы решения иррациональных уравнений.

1) Возведение обеих частей уравнения в одну и ту же степень:

а) Для четной степени

1-й способ: Переход к равносильной системе: =g(x)

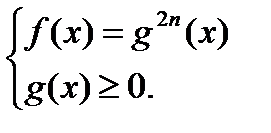
2-й способ: + проверка

б) Для нечетной степени: =g (x)

Пример 1:

Ответ: 3.

Пример 2: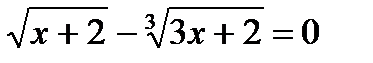

Уединим радикал и возведем в 6 степень

Проверкой убеждаемся, что х=-1 – посторонний корень

Ответ: 2.

2) Введение новой переменной (подстановка)

Пример: 2 + =3

Пусть у= (у 0), тогда получим уравнение

2у²+у-3=0

у₁=1, у₂ = - 0 – не подходит по условию.

Обратная замена: = 1

Возведем обе части уравнения в 6-ю степень:

х+1=1

х=0

Ответ: 0

3) Разложение на множители

Для решения иррациональных уравнений данным методом следует пользоваться правилом:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей, входящих в произведение, равен нулю, а остальные при этом имеют смысл.

Пример: (х-3) = 2х-6

(х-3) -(2х-6)=0

(х-3) - 2(х-3)=0

Разложим на множители:

(х-3)( - 2)=0, тогда

или – 2=0

или =4

или х=0 или х=5

Ответ: 0; 5

4) Использование монотонности функции входящих в уравнение

(функциональный метод)

Использование монотонности функций, входящих в уравнение, нередко значительно упрощают техническую часть решения.

Сформулируем два свойства монотонных функций:

1. Сумма возрастающих (убывающих) функций - функция возрастающая (соответственно, убывающая) на их общей области определения.

2. Разность возрастающей и убывающей (соответственно, убывающей и возрастающей) функций - функция возрастающая (убывающая) на их общей области определения.

Пример 1:

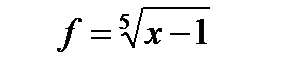возрастает, возрастает, их сумма возрастает на области определения.

h= убывает на D(h), следовательно уравнение имеет 1 корень. Подбором находим x=2.

Ответ: 2

Пример 2: Найти количество корней уравнения .

возрастает на ОДЗ, возрастает на ОДЗ,

их сумма тоже возрастает, а (4-х) убывает,

следовательно уравнение имеет 1 корень.

5) Метод перехода к уравнению с модулем

Если при решении иррационального уравнения можно избавиться от знака корня четной степени, то получается уравнение, содержащее знак модуля, т.е. используются формулы

Пример:

+ =6

+ =6

+ =6

Полученное уравнение можно решить методом интервалов или с использованием свойств модуля.

6) Метод введения вспомогательных переменных.

Пример:

то

Тогда получим систему: