Трубоповод с непрерывным путевым расходом.

Определим потери напора на участке АВ с непрерывным путевым расходом -транзитный; - путевой.

Расход в некотором произвольном сечении этого участка С, расположенном на расстоянии Х от начального сечения А, будет меньше расхода в сечении А, равного + , на величину отбора по длине и составит

.

Полагая по прежнему, что движение жидкости происходит в квадратичной области турбулентного режима, для потери напора на элементарном участке трубопровода длиной у сечения С будем иметь

.

Интегрируя далее это выражение в пределах от 0 до L, получим расчетную формулу для определения потери напора на всем участке трубопровода длиной L, на котором имеет место непрерывный путевой расход,

,

или окончательно

.

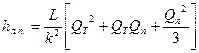В частном случае, когда на участке L отбирается весь расход, т.е. транзитный расход 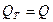, потеря напора будет .

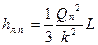Это формула известна под названием формулы Дюпюи. Из нее следует, что потери напора в трубопроводе при непрерывном путевом расходе оказываются в 3 раза меньше той потери напора, которая имела бы место при отсутствии путевой раздачи и таком же расходе, полностью сосредоточенном в конце трубопровода.

Лекция 16. Неустановившееся движение жидкости. Гидравлический удар. Формула Жуковского. Способы ослабления гидравлического удара. Определение скорости распространения ударной волны.

Неустановившееся движение воды с переменным вдоль пути расходом широко распространено в водопроводно-канализационных сооружениях.

Учение о гидравлических жидкостях с переменным вдоль пути расходом основано на дифференциальных уравнениях движения тела с переменной массой, выделенных И. В. Мещерским. По предложению Конакова основное дифференциальное уравнение движения тела с переменной массой можно представить в виде

,

где М- масса тела, являющаяся функцией t, x, y и z;

V- скорость движения тела переменной массы в направлении основного движения;

V₁ – проекция скорости движения присоединяемой массы на направление основного движения равнодействующих всех внешних сил, действующих на тело переменной массы;

S – путь движения тела с переменной массой.

При выводе уравнения принято, что присоединение или отделение массы распределено равномерно по всему сечению.

Рассмотрим отсек жидкости длиной ds и площадью поперечного сечения с переменным вдоль пути расходом. На отсек жидкости действуют сила тяжести, силы гидродинамического давления слева и справа и сила трения.

Изменение кинетической энергии за время dt

, (1)

так как .

Спроецируем все силы на направление движения, то есть на оси s.

Проекция силы тяжести , но так как , , то получим .

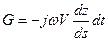Разность проекций сил гидродинамического давления 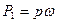и равна: .

Проекция сил трения ,

где - напряжение сил трения;

Х- длина смоченного периметра.

Изменение массы за время dt без учета бесконечно малых величин высшего порядка .

Подставляя полученные выражения в основное дифференциальное уравнение (1) получим

.

Учитывая, что 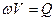и разделив все члены вышеприведенного уравнения на , получим .

Отношение проекции скорости V₁ присоединяемой или отделяемой массы на направление движения к проекции скорости основного потока обозначим через m. Учитывая, что , и перенеся левую часть получим

.

Преобразуем полученное уравнение следующим образом.

Первые два слагаемых представим в виде

.

С учетом того, что , правая часть приведенного выше уравнения приобретает вид .

В условиях неустановившегося движения

;

.

С учетом этих зависимостей можно записать, что правая часть рассматриваемого уравнения равна

.

Подставив полученное выражение в (2) и сократив все члены уравнения на Q, получим

(3).

Отношение , а множитель .

Подставляя это выражение в уравнение (3) получим

(4).

В связи с тем, что координата z не зависит от времени и является только функцией пути, в уравнение (4) производится замена .

После интегрирования уравнения (4) получим уравнение ,

где (5).

Последнее выражение представляет собой развернутое основное уравнение движения жидкости с переменной массой вдоль пути в условиях неустановившегося движения.