
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Исследование режимов работы генератора Чуа
|
|
Обезразмеренная система уравнений для генератора Чуа имеет вид

где f(x) – вольт-амперная характеристика (ВАХ) отрицательного сопротивления. В рассматриваемом примере f(x) взята в виде:

График этой функции изображен ниже на рисунке 1.

Рисунок 1
Представлены результаты расчета в программе MatLab, для решения используются одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка с автоматическим выбором шага.
Рассматриваются три решения задачи с различными начальными условиями.
На рисунке 2 представлены фазовые портреты генератора в плоскостях (х0у), (x0z) и (y0z) соответственно по порядку сверху вниз при начальных условиях x0=0.5, y0=0.5, z0=0.5.
Код программы:
% генератор Чуа
clc; clear;
t = [0 25]; %временной интервал
X01 = [0.5 0.5 0.5]; %начальные условия 1
X02 = [0.5 0.5 0.6]; %начальные условия 2
%% решение системы, записанной в " f_Chua"
[t, X1]=ode45('f_Chua', t, X01);
x1 = X1(:, 1); y1 = X1(:, 2); z1 = X1(:, 3);
[t, X2]=ode45('f_Chua', t, X02);
x2 = X2(:, 1); y2 = X2(:, 2); z2 = X2(:, 3);
function Ch=f_Chua(t, x)
alpha = 16; beta = 13.3;
Ch = [ alpha*(x(2)-x(1)-f_vah(x(1)));
x(1)-x(2)+x(3);
-beta*x(2)];
function fx=f_vah(x)
gamma = 4;
if abs(x)< 6
fx = -gamma*sin(0.4*x);
else
fx = 0;
end

Рисунок 2
Теперь такие же графики для второй задачи с начальными условиями x0=0.5, y0=0.5, z0=0.55.
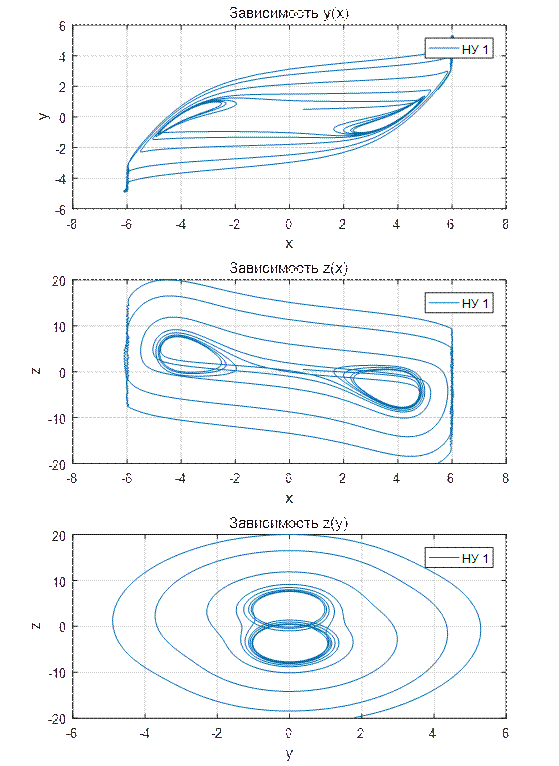
Рисунок 3
И, наконец, графики для третьей задачи с начальными условиями x0=0.5, y0=0.5, z0=0.6.

Рисунок 4
По представленным на рисунках графикам видно как меняется характер решения при изменении начальных условий. Видно, что генератор работает только при начальных условиях 1 и 2 (см. рисунки 3, 4, при увеличении времени анализа траектория сходится к замкнутой кривой).
Посмотрим на параметр, который характеризует степень разбегания траекторий d(t). На графике, изображенном на рисунке 5 видно как сильно разбегаются траектории первого и второго решения со временем.

Рисунок 5
Рассмотрим теперь влияние крутизны ВАХ, для этого увеличим значение  в программе, например, на 0.01, функция будет иметь вид:
в программе, например, на 0.01, функция будет иметь вид:

На рисунке 6 и 7 представлены фазовые портреты в тех же плоскостях что и ранее при двух начальных условиях. На рисунке 8 изображен график, характеризующий степень разбегания траекторий.

Рисунок 6

Рисунок 7

Рисунок 8
По рисункам видно, что графики значительно различаются.
При уменьшении крутизны ВАХ, т.е. при уменьшении параметра  , фазовые портреты для двух начальных условий почти не различаются. Это соответствует ожиданиям, т.к. в данном случае существует только одна устойчивая точка.
, фазовые портреты для двух начальных условий почти не различаются. Это соответствует ожиданиям, т.к. в данном случае существует только одна устойчивая точка.
Графики фазовых портретов изображены на рисунке 9, а график разбега траекторий - на рисунке 10, по которому видно, что разбег траекторий не велик и максимальное значение разбега меньше единицы, в то время как раньше оно было около 30.

Рисунок 9

Рисунок 10
|