
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Найдем расход жидкости по закону Дарси
|
|
 .
.
Поскольку при установившемся движении несжимаемой жидкости расход Q сохраняется вдоль оси r струйки, имеем
 , т.е.
, т.е.  .
.
Так как k, m, h и j - постоянные, поэтому получаем
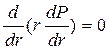 (3.18)
(3.18)
или в развернутом виде
 . (3.19)
. (3.19)
Это есть дифференциальное уравнение Лапласса в полярных координатах для установившегося плоскорадикального потока несжимаемой жидкости по закону Дарси.
Дважды интегрируя уравнение (3.18), находим его общее решение
 или
или  , откуда
, откуда
Р=С1lnr+С1. (3.20)
 Постоянные интегрирования С1 и С2 находим из граничных условий, которые в данном случае имеют вид:
Постоянные интегрирования С1 и С2 находим из граничных условий, которые в данном случае имеют вид:
при r = rc P = Pc = const;
при r = rk P = Pk = const. (3.21)
Подставляя граничные условия (3.21) в общее решение (3.20), находим
Pc = C1lnrc + C2;
Pk = C1lnRk + C2,
откуда
 (3.22)
(3.22)
 (3.23)
(3.23)
Подставляя (3.22) и (3.23) в общее решение (3.20), находим закон распределения давления в плоскорадиальном потоке:
 ,
,
или  . (3.24)
. (3.24)
Из выражений (3.24) следует, что давление в пласте распределяется по логарифмическому закону в зависимости от расстояния r точки до оси скважины; вращением кривой P = P(r) вокруг оси скважины образуется поверхность, называемая воронкой депрессии (рис.11). Воронка депрессии имеет большую крутизну вблизи скважины. Следовательно, основная часть депрессии на пласт сосредоточена в призабойной зоне скважины, параметры которой сильно влияют на дебит скважины.

Рис.11 Рис.12
Изобарами (линиями равного давления) являются концентрические окружности ортогональные траекториям, совпадающими с радиусами указанных окружностей (рис.12).
Градиент давления находим из выражения
 .
.
Подставляя значение С1 из (3.22),
находим  . (3.25)
. (3.25)
Тогда скорость фильтрации и дебит скважины соответственно
 . (3.26)
. (3.26)
 ,
,
откуда
 . (3.27)
. (3.27)
Формулу (3.27) называют формулой Дюпюи.
Как следует из формул (3.25) и (3.26), градиент давления dP/dr и скорость фильтрации V в любой точке пласта обратно пропорциональны расстоянию r от этой точки до оси скважины (гиперболический закон). Из графика (рис.13) видно, что при приближении к скважине градиент давления и скорость фильтрации резко возрастают, достигая максимального значения на стенке скважины. Этот вывод очевиден из самого определения скорости фильтрации как отношения объемного расхода жидкости к площади фильтрационной поверхности, т.е.
 .
.

Рис. 13 Рис.14
Дебит скважины, как это следует из формулы Дюпюи (3.27), прямо пропорционален перепаду давления DР = Рк - Рс и одинаков через любую цилиндрическую поверхность, соосную скважине, т.е. от r не зависит. На основании этой же формулы (3.27) можно отметить слабую зависимость дебита скважины Q от изменения значений Rk и rc, поскольку последние входят под знак логарифма. Практическое значение этого факта состоит в том, что:
а) неизвестность точного значения радиуса контура питания Rк не вводит значительных погрешностей в расчет дебита скважины;
б) практически невозможно достигнуть значительного увеличения дебита скважины Q за счет увеличения ее радиуса rс.
Расчетная формула Дюпюи (3.27) позволяет определить коэффициент проницаемости пласта k промысловым методом.
График зависимости дебита скважины Q от перепада давления на скважине DРс = Рк - Рс называется индикаторной диаграммой; которая в рассматриваемом потоке представляется прямой линией (рис.14). Индикаторная диаграмма характеризует продуктивность скважины и помогает устанавливать режим работы скважины.
Отношение дебита скважины Q к перепаду давления DРс называется коэффициентом продуктивности К, выражение которого находится из формулы (3.27)
 . (3.28)
. (3.28)
Размерность: 
Определив промысловым методом коэф. продуктивности К, можно вычислить гидропроводность пласта e
 , (3.29)
, (3.29)
или, в частности, коэффициент проницаемости

 , т.е.
, т.е.  , (3.30)
, (3.30)
что непосредственно вытекает из формулы Дюпюи (3.27).
Найдем закон движения частиц жидкости. Из известной нам зависимости
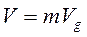 , т.е.
, т.е.  ,
,
находим
 .
.
Интегрируя в пределах от 0 до t и, соответственно, от R0 до r, получаем закон движения частиц жидкости
 ;
; 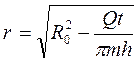 . (3.31)
. (3.31)