
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциал функции. Понятие дифференциала функции.
|
|
МИНОБРНАУКИ РОССИИ
Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Балтийский федеральный университет имени Иммануила Канта» (БФУ им. И.Канта)
Институт природопользования, территориального развития
И градостроительства
Еремина Л.А.
Математика
Методические указания по выполнению контрольной работы
Для студентов заочной формы обучения
Специальность:
08.02.08 «Монтаж и эксплуатация оборудования и систем газоснабжения»
2014 г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Контрольное задание имеет 100 вариантов.
Вариант выбирается по двум последним цифрам шифра студента. Так, если номера шифра 12, 105, 200, 1180, то соответственно две последние цифры определяют номера вариантов: 12, 05, 00, 80. Студенты, у которых номера шифров от 1 до 9, должны добавлять к своему номеру слева ноль и выполнять примеры и задачи соответственно из вариантов 01, 02, …, 09. Номера заданий указаны в таблице.
Контрольную работу следует выполнять в отдельной тетради, на тетрадь наклеивается титульный лист, на котором указывается номер контрольной работы, наименование дисциплины, фамилия, имя, отчество, шифр студента.
Контрольная работа должна быть выполнена аккуратно и разборчиво, чертежи выполнены с помощью чертежных инструментов.
Условия заданий необходимо переписывать полностью, решения должны сопровождаться краткими и достаточными объяснениями, используемые формулы нужно выписывать.
В конце работы следует указать литературу, которой вы пользовались, проставить дату выполнения работы и подпись.
Студенты должны ознакомиться с рецензией преподавателя, исправить все допущенные в работе ошибки, а в случае неудовлетворительного выполнения работы выполнить ее заново и представить на проверку вместе с незачтенной работой.
ЛИТЕРАТУРА
1. Математика для техникумов. Алгебра и начала анализа под редакцией Яковлева Г.Н., ч. 1 – М.: Наука, 1987
2. Математика для техникумов. Алгебра и начала анализа под редакцией Яковлева Г.Н., ч. 2 – М.: Наука, 1988
3. Валуцэ И.И., Димегул Т.Д. Математика для техникумов на базе средней школы. – М.: Наука, 1989
4. Богомолов Н.В. Практические задания по математике. – М.: Высшая школа, 2000
СОДЕРЖАНИЕ КУРСА
Тема 1.1 Функция. Предел функции. Непрерывность функции.
Предел функции
Число А называется пределом функции ƒ (х) при х  а, если для любого х, удовлетворяющему неравенству
а, если для любого х, удовлетворяющему неравенству  < б, выполняется неравенство l ƒ (х) – Аl < Е. В этом случае пишут
< б, выполняется неравенство l ƒ (х) – Аl < Е. В этом случае пишут 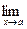 ƒ (х) = А.
ƒ (х) = А.
Для функций, имеющих предел, справедливы следующие свойства:
1. 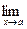 (ƒ (х) ± g(х)) =
(ƒ (х) ± g(х)) = 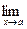 ƒ (х) ±
ƒ (х) ± 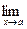 g(х);
g(х);
2. 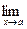 ƒ (х) * g(х) =
ƒ (х) * g(х) = 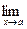 ƒ (х) *
ƒ (х) * 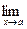 g(х);
g(х);
3. 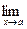
 =
= 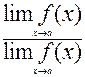 , если
, если 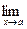 g(х)
g(х) 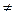 0;
0;
Следствие: постоянный множитель можно выносить за знак предела.
Функция ƒ (х) называется бесконечно малой при х  а, если
а, если 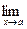 f(x) = 0.
f(x) = 0.
Функция ƒ (х) называется бесконечно большой при х  а, если
а, если 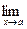 f(x) =
f(x) = 
Свойства бесконечно малых и бесконечно больших функций:
1. Если ƒ (х) и g(x) – бесконечно малые при х  а, то их сумма ƒ (х) + g(x) при х
а, то их сумма ƒ (х) + g(x) при х  а также бесконечно малая функция.
а также бесконечно малая функция.
2. Если ƒ (х) при х  а бесконечно малая, а F(x) – ограниченная функция, то произведение ƒ (х)* F(x) – функция бесконечно малая.
а бесконечно малая, а F(x) – ограниченная функция, то произведение ƒ (х)* F(x) – функция бесконечно малая.
3. Если при х  а ƒ (х) имеет конечный предел, а g(x) – бесконечно большая, то
а ƒ (х) имеет конечный предел, а g(x) – бесконечно большая, то 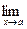 (ƒ (х) + g(x)) =
(ƒ (х) + g(x)) =  ,
, 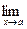
 =0
=0
4. Если ƒ (х) бесконечно малая при х  а, то
а, то  - бесконечно большая; наоборот, если при х
- бесконечно большая; наоборот, если при х  а ƒ (х) бесконечно большая, то
а ƒ (х) бесконечно большая, то  - бесконечно малая.
- бесконечно малая.
Если предел делителя равен нулю, а предел делимого есть число отличное от нуля, то предел дроби имеет бесконечный предел.
Пример: 
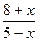 ; предел делителя
; предел делителя  (5-х) = 0, предел числителя
(5-х) = 0, предел числителя  (8+х) = 13. Функция (5-х) при х
(8+х) = 13. Функция (5-х) при х  5 – бесконечно малая, следовательно, функция
5 – бесконечно малая, следовательно, функция 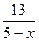 при х
при х  5 – бесконечно большая, т.е.
5 – бесконечно большая, т.е. 
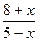 =
=  .
.
Если предел делимого существует, а предел знаменателя равен  , то предел дроби равен нулю.
, то предел дроби равен нулю.
Пример: 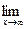
 ; предел делителя при х
; предел делителя при х  равен
равен  , следовательно,
, следовательно, 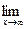
 = 0, т.к.
= 0, т.к.  - бесконечно малая функция.
- бесконечно малая функция.
Иногда при подстановке в функцию предельного значения аргумента получатся выражения, не имеющие конкретного смысла:  ,
,  , их называют «неопределенностями». В этих случаях для нахождения пределов необходимо выполнить необходимые преобразования или применить правило:
, их называют «неопределенностями». В этих случаях для нахождения пределов необходимо выполнить необходимые преобразования или применить правило:
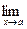
 =
= 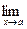
 .
.
Пример 1. 
 =
= 
 =
=  х = 1.
х = 1.
Пример 2. 
 =
= 
 =
= 
 =
=  2
2  = 2
= 2 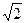 .
.
При нахождении предела функции иногда приходиться применять замечательные пределы.
Первый замечательный предел: 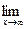 (1+
(1+ 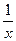 )
) 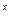 = е или
= е или 
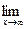 (1+х)
(1+х)  = е.
= е.
Второй замечательный предел: 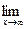
 = или:
= или: 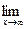
 =;
=;
Пример 3. 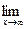 (1+
(1+  =
= 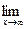 (1+
(1+  = е
= е  .
.
Пример 4. 
 =
= 
 =
= 
 =
= 
 =
=  =
= 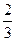 *1*1 =
*1*1 = 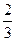 .
.
Тема 1.2. Производная и дифференциал функции, их приложения к решению прикладных задач
Производная.
Пусть функция y = f(x) определена на промежутке (а, в). Из этого промежутка возьмем два значения x и x  , тогда x - x
, тогда x - x  = Δ x называется приращением аргумента, а f(x) – f(x
= Δ x называется приращением аргумента, а f(x) – f(x  ) = Δ y приращением функции. Тогда предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремиться к нулю, называется производной и обозначается: f´ (x) =
) = Δ y приращением функции. Тогда предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремиться к нулю, называется производной и обозначается: f´ (x) = 
 или y´ =
или y´ = 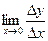 .
.
Если функция f(x) имеет производную в точке x  , то она называется дифференцируемой в этой точке.
, то она называется дифференцируемой в этой точке.
Если функция f(x) имеет производную в каждой точке промежутка (а, в), то она называется дифференцируемой на этом промежутке.
Пусть y = f(u), где u является не зависимой переменной, а функцией независимой переменной х:
u = 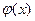 , тогда функция y = f(
, тогда функция y = f(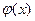 ) называется сложной, а u промежуточным аргументом.
) называется сложной, а u промежуточным аргументом.
Правило дифференцирования сложной функции:
Если y = f(u) u = 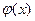 дифференцируемые функции своих аргументов, то производная сложной функции y = f(
дифференцируемые функции своих аргументов, то производная сложной функции y = f(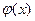 ) существует и равна произведению производной функции y по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной х:
) существует и равна произведению производной функции y по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной х:
y´ (x) = y´ (u) * u´ (x).
Формулы дифференцирования:
1. c´ = 0
2. x´ = 1
3. (u ± v)´ = u´ ± v´
4. (u * v)´ = u´ v + uv´
5. 

6.  Сложная функция:
Сложная функция:
7. 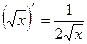 6а. (u)
6а. (u)  = nu
= nu 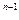 u´
u´
8.  7a.
7a. 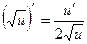
9. 
 8a.
8a. 
10.  9a.
9a. 
11.  10a.
10a. 
12.  11a.
11a. 
13. 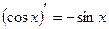 12a.
12a. 
14. 
 13a.
13a. 
15.  14a.
14a. 
16.  15a.
15a. 
17.  16a.
16a. 
18. 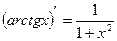 17a.
17a. 
19.  18a.
18a. 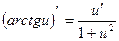
19a. 
Пример 1. Найти производную функции y =  .
.
Применяем формулы 2, 3, 6.
Решение: y = 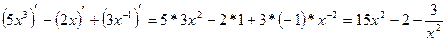 .
.
Пример 2. Найти производную функцию y =  .
.
Решение. Применяем формулы 1, 3, 5, 6.
y =  =
=  =
= 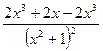 =
=  ;
;
Пример 3. найти производную функции y = sin  и вычислить ее значение при
и вычислить ее значение при  . Решение: Эта сложная функция с промежуточным аргументом sin
. Решение: Эта сложная функция с промежуточным аргументом sin 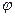 . Используя формулы 6а и 12, имеем y
. Используя формулы 6а и 12, имеем y 
Пример 4. Найти производную функции 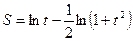
Теперь дифференцируем по формулам 3, 10, 10а, 6, 1:
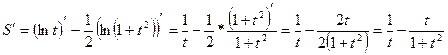 ;
;

Геометрический смысл производной.
Если функция y = f(x) дифференцируема в точке х, то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке, т.е.  .
.
Уравнение касательной имеет вид: y-y  =
=  .
.
Пример 5. Составить уравнение касательной к графику функции y = 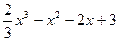
в точке с абсциссой х = 3.
Решение: Найдем производную функции: 
найдем произведение производной при х = 3: 
найдем значение функции при х = 3: 

Уравнение касательной имеет вид: y-6 = 10 *(x-3) или y-6 = 10x-30, т.е. 10x-y-24=0.
Физический смысл производной.
При прямолинейном движении точки скорость  в данный момент времени t-t
в данный момент времени t-t  есть производная пути, вычисленная при t = t
есть производная пути, вычисленная при t = t  , т.е.
, т.е.  (t) =
(t) = 

Пример 6. Тело движется по закону S´ (t) =  (м). Найти скорость движения в конце первой секунды.
(м). Найти скорость движения в конце первой секунды.
Решение: Найдем скорость тела в момент времени t  (t) =
(t) = 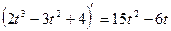 ,
,  (1) = 15-6 =9 (м/с).
(1) = 15-6 =9 (м/с).
Вторая производная и ее физический смысл.
При прямолинейном движении точки ускорение, а в данный момент времени t=t  есть производная скорости
есть производная скорости  или вторая производная пути, вычисленная при t=t
или вторая производная пути, вычисленная при t=t  , т.е. a =
, т.е. a =  или a =
или a = 

Пример 7. Найти вторую производную функции  и вычислить ее значение при x = 2.
и вычислить ее значение при x = 2.
Решение: Сначала найдем первую производную:  =
= 
 .
.
Найдем вторую производную: 
Вычислим значение второй производной при x = 2.

Пример 8. Точка движется по прямой по закону  .
.
Найти скорость и ускорение движения при  .
.
Решение: Находим скорость в момент  .
.
 тогда
тогда  Находим ускорение в момент
Находим ускорение в момент  ,
,  , тогда
, тогда 
Приложение производной к исследованию функций.
Чтобы построить график функции, нужно познакомиться с приложением производной к исследованию монотонности и экстремума функции, на нахождение промежутков выпуклости и точек перегиба. При исследовании функции на монотонность необходимо применить достаточное условие возрастание и убывания функции: если дифференцируемая функция y = f(x) имеет положительную производную на промежутке (a; в), то она возрастает на этом промежутке; если y = f(x) имеет отрицательную производную на промежутке (a; в), то она убывает на этом промежутке.
При исследовании функции на экстремум необходимо применить необходимое и достаточное условие экстремума.
Достаточное условие экстремума. Если функция y = f(x) имеет экстремум при 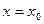 , то ее производная в этой точке равна нулю или бесконечности, или вовсе не существует, при этом сама функция в этой точке определена.
, то ее производная в этой точке равна нулю или бесконечности, или вовсе не существует, при этом сама функция в этой точке определена.
Точки, в которых производная равна нулю или бесконечности, или не существует, называется критическими. Необходимое условие экстремума позволяет определить критические точки. Для уточнения, какая из найденных точек является экстремальной, необходимо воспользоваться достаточным условием экстремума.
Достаточное условие экстремума:
Пусть функция y = f(x) дифференцируема в окрестности критической точки 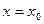 , кроме, возможно, самой точки
, кроме, возможно, самой точки  . Тогда:
. Тогда:
1. если при переходе через  производная меняет знак с плюса на минус, то в этой точке функция имеет максимум;
производная меняет знак с плюса на минус, то в этой точке функция имеет максимум;
2. если при переходе через  производная меняет знак с минуса на плюс, то в этой точке функция имеет минимум;
производная меняет знак с минуса на плюс, то в этой точке функция имеет минимум;
3. если при переходе через  производная не меняет знак, то в этой точке нет экстремума.
производная не меняет знак, то в этой точке нет экстремума.
При исследовании функции на выпуклость необходимо применить достаточное условие выпуклости графика функции.
Достаточное условие выпуклости: график дифференцируемой функции y = f(x) является выпуклым вверх на промежутке (a; в), если  < 0 на этом промежутке; и выпуклым вниз на промежутке (a; в), если
< 0 на этом промежутке; и выпуклым вниз на промежутке (a; в), если  > 0 на этом промежутке.
> 0 на этом промежутке.
График функции y = f(x) может иметь два и более промежутков выпуклости. Точки, являющиеся концом одного промежутка выпуклости и началом другого, называются точками перегиба.
Необходимое условие существования точки перегиба:
если дифференцируемая функция y = f(x) имеет точку перегиба при 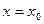 , то
, то  .
.
Достаточное условие существования точки перегиба:
если при переходе через  вторая производная функции y = f(x) меняет знак, то
вторая производная функции y = f(x) меняет знак, то  является точкой перегиба.
является точкой перегиба.
Общая схема исследования функций и построения их графиков:
· Найти область определения функции.
· Исследовать функцию на четность и нечетность.
· Найти точки пересечения графика функции с осями координат.
· Найти промежутки монотонности и экстремумы функции.
· Найти промежутки выпуклости и точки перегиба графика функции.
· Построить график функции, используя все полученные результаты исследования. Если их окажется недостаточно, то следует найти еще несколько точек графика функции, исходя из ее уравнения.
Пример 9. Построить график функции  .
.
Решение: 1. Областью определения функции служит множество действительных значений, т.е. Д(y) = R.
2. Исследуем на четность и нечетность функцию:
F(-x) = 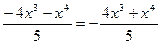 , т.е. f(-x)
, т.е. f(-x)  ,
,  . Значит, функция не является четной и нечетной.
. Значит, функция не является четной и нечетной.
3.Найдем очки пересечения графика функции с осями координат:
ОХ: y=0, y=0, y=0, y=0

 ,
,  , x=0, x=4
, x=0, x=4
OY:  x=0
x=0
y=0
4. Найдем промежутки монотонности и экстремумы функции:

 или 3-х=0, х=3.
или 3-х=0, х=3.
Критические точки первого рода х=0 и х=3 отмечаем на числовой прямой и определяем знак первой производной в промежутках, на которые разбивают критические точки область определения функции.
Функция возрастает на промежутке  и убывает на промежутке
и убывает на промежутке  .
.
При переходе через х = 3 производная изменила знак с (+) на (-), следовательно в этой точке функция имеет максимум.

5.Исследуем функцию на выпуклость и точки перегиба: 
Находим критические точки: 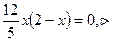 x =0 или х=2.
x =0 или х=2.
Критические точки х=0 и х=2 разбивают область определения функции на промежутки, определяем знак второй производной в каждом промежутке:
На промежутках  и
и  график функции выпуклый вверх; на промежутке (0; 2) график функции выпуклый вниз.
график функции выпуклый вверх; на промежутке (0; 2) график функции выпуклый вниз.
При переходе через точки х=0 и х=2 вторая производная поменяла знак, следовательно, эти точки являются точками перегиба.
y(0)=0; y(2)= 
(0; 0), (2; 3, 2) – точки перегиба.
Найдем дополнительную точку графика функции: y(-1) = -1.
Все точки отмечаем на координатной плоскости и соединяем их плавной линией.
Нахождение наибольшего и наименьшего значений функции.
Нахождение наибольшего и наименьшего значений непрерывных функций основано на следующих свойствах:
1) если в некотором промежутке (а; в) функция y = f(x) непрерывна и имеет только один экстремум и если это максимум, то он и является наибольшим значением функции, а если минимум – наименьшее значение функции в этом промежутке;
2) если функция y = f(x) непрерывна на отрезке  , то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри отрезка, или на концах этого отрезка.
, то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри отрезка, или на концах этого отрезка.
Поэтому, чтобы найти наибольшее и наименьшее значения функции на  , где она непрерывна, следует:
, где она непрерывна, следует:
1. Найти экстремумы функции на данном отрезке.
2. Найти значен6ия функции на концах отрезка: f(a), f(в).
3. Из всех найденных значений выбрать наибольшее и наименьшее.
Пример 10. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 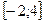 .
.
Решение: 1. Найдем экстремумы функции


x 
x=0 или 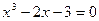

x=-1, x=3
 функция имеет максимум
функция имеет максимум
 функция имеет максимум
функция имеет максимум
 функция имеет минимум
функция имеет минимум
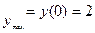



2. Найдем значения функции на концах отрезка:
 ,
, 
наибольшее значение:  наименьшее значение:
наименьшее значение: 
Пример 11. требуется изготовить ящик с крышкой, стороны основания которого относятся как 1: 2, а площадь полной поверхности 108  . Какими должны быть его размеры, чтобы его объем был наибольшим?
. Какими должны быть его размеры, чтобы его объем был наибольшим?
Решение: необходимо определить стороны основания а и в и высоту h прямоугольного параллелепипеда, чтобы при этих значениях его объем был наибольшим.
Пусть, а = х, т.к. а: в = 1: 2, то в = 2x. Объем V = a*h*в = 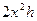 .
.
Надо выразить h через x и площадь полной поверхности S=108.
S = 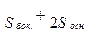 ;
; 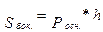 ;
;  .
.

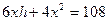

Тогда V = 
Наибольшее значение функции и следует определить.
1. Область определения функции V является только положительные значения х, т.е. х> 0.
2. Находим производную: V´ = 0; 36-4x  =0, x = ±3.
=0, x = ±3.
3. Находим вторую производную:  функция имеет максимум.
функция имеет максимум.
4. a = 3, в = 6, h = 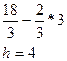
Следовательно, объем ящика будет наибольшим, если стороны его основания 3 см и 6см, а высота h = 4 см.
Дифференциал функции. Понятие дифференциала функции.
По определению производной имеем  ƒ ´ (x)=
ƒ ´ (x)= 
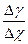 .
.
Из теории пределов известно, что 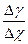 = ƒ ´ (x) + ά (Δ x), где ά (Δ х)- бесконечно малая величина. Выразим Δ у: Δ у = ƒ ´ (х)*Δ х+ ά (Δ х)*Δ х,
= ƒ ´ (x) + ά (Δ x), где ά (Δ х)- бесконечно малая величина. Выразим Δ у: Δ у = ƒ ´ (х)*Δ х+ ά (Δ х)*Δ х,  ά (Δ x)*Δ x=0. Следовательно, Δ у ≈ ƒ ´ (х) *Δ х. Выражение ƒ ´ (х) Δ х назвали главной частью приращения функции, или дифференциалом функции. Дифференциал функции обозначается dy = ƒ ´ (x)*Δ x. В частности, если ƒ ´ (х) = х, то dy = 1* Δ x или dy = dх, тогда dy = ƒ ´ (x) dх.
ά (Δ x)*Δ x=0. Следовательно, Δ у ≈ ƒ ´ (х) *Δ х. Выражение ƒ ´ (х) Δ х назвали главной частью приращения функции, или дифференциалом функции. Дифференциал функции обозначается dy = ƒ ´ (x)*Δ x. В частности, если ƒ ´ (х) = х, то dy = 1* Δ x или dy = dх, тогда dy = ƒ ´ (x) dх.
Пример 12. Найти дифференциал функции у = (2х³ -4) 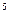

 .
.
Решение: dy = ((2х³ -4) 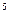 )´ dх
)´ dх
dy = 5 (2х³ -4)  * (2х³ -4)´ dх
* (2х³ -4)´ dх
dy = 5(2х³ -4)  *6х² dх
*6х² dх
dy = 30х² (2х³ -4)  dх
dх
Пример 13. Вычислить значение дифференциала функции V = cos³ 3y при у = 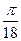
 , Δ у = 0, 01.
, Δ у = 0, 01.
Решение. Дифференциал функции вычисляется по формуле dv = v´ (y) dy.
dV = (cos³ 3y)´ dy; dV = 3cos³ 3y* (cos 3y)´ dy.
dV = 3cos² 3y *(-sin 3y)*(3y)´ dy.
dV = -9 cos² 3y* sin 3y dy.
dV = -9 cos² 3 * 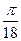 *sin 3 *
*sin 3 * 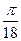 * 0, 01 = -9 cos²
* 0, 01 = -9 cos²  *sin
*sin  * 0, 01 = -9 (√ 3/2)² *
* 0, 01 = -9 (√ 3/2)² *  *0, 01 = -
*0, 01 = -  * 0, 01 = -3, 375 * 0, 01 = 0, 03375.
* 0, 01 = -3, 375 * 0, 01 = 0, 03375.
Приложение дифференциала к приближенным вычислениям.
Приращение функции связано с дифференциалом функции следующим соотношением:
Δ у ≈ dy.
Пример 14. Вычислить приближенное значение приращения функции у = х² +2х+5 при изменении аргумента от х = 2 до х = 2, 001.
Решение. Находим дифференциал функции:
dy = (х² +2х+5)´ dx. dy = (2x+2) dx.
Находим приращение аргумента: Δ х = 2, 001 – 2= 0, 001, тогда dy = (2*2+2)*0, 001= 0, 006 и Δ y ≈ 0, 006.
Пример 15. Вычислить приближенное значение функции у = х³ +х² -2х при х = 2, 01.
Решение: Для нахождения приближенного значения функции воспользуемся формулой: ƒ (х۪ +Δ х) ≈ ƒ (х۪) +dy.
В нашем примере х۪ + Δ х = 2, 01, следовательно, х۪ = 2, Δ х = 0, 01.
Сначала найдем значение функции в точке х۪ = 2.
ƒ (2) = 2³ +2² -2*2 = 8. Затем найдем дифференциал функции dy= (x³ +x² -2x)´ dx, dy = (3x² +2x-2)dx и вычислим дифференциал при х۪ =2 и Δ х=0, 01.
dy = (3*2² +2*2-2)* 0, 01 = 0, 14, следовательно, ƒ (2, 01) ≈ 8+0, 14 = 8, 14.
Пример 16. Найти приближенное значение 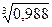
Решение: Нам надо найти приближенное значение функции у =  при х = 0, 988; dx = Δ х = 0, 988-1= - 0, 012.
при х = 0, 988; dx = Δ х = 0, 988-1= - 0, 012.
ƒ (0, 988) ≈ ƒ (1) + dy
ƒ (1) = 
dy = ( )´ dx =
)´ dx =  *
* 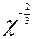 dx =
dx =  =
=  ;
;
dy = 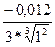 = - 0, 004
= - 0, 004
Тогда 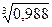 ≈ 1 – 0, 004 = 0, 996.
≈ 1 – 0, 004 = 0, 996.
Пример 17. Объем куба, ребро которого равно 4см при нагревании увеличилось на 0, 96 см³. как при этом увеличилось ребро куба?
Решение: объем куба с ребром х вычисляется по формуле V = х³. Так как Δ V ≈ dy, то dV ≈ 0, 96 см³. Дифференциал функции вычисляем по формуле: dV = V´ dx, следовательно, dx = dV/V´.
Найдем V´ = (x³)´ = 3x²; V´ (4) = 3*4² = 48.
Тогда, dx = 0, 96/48 = 0, 02; Δ х = dx = 0, 02 см, т. е. ребро куба увеличилось на 0, 02см.
Тема 1.3 Интеграл и его приложения. Неопределённый интеграл
Понятие неопределённого интеграла.
Дифференцирование- это действие, с помощью которого по данной функции находиться её производная или дифференциал. Так, по данному закону движения тела S=S(t) мы путём дифференцирования находим скорость 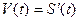 , а затем и ускорение
, а затем и ускорение  . По данному уравнению кривой
. По данному уравнению кривой  определяли угловой коэффициент касательной, проведённой к этой кривой:
определяли угловой коэффициент касательной, проведённой к этой кривой: 
На практике часто приходиться решать обратную задачу: по известной скорости движения тела устанавливать закон его движения, по данному угловому коэффициенту касательной к кривой находить её уравнение. Иначе говоря, по данной производной отыскивать функцию, от которой найдена эта производная, т.е. выполнять действие, обратное дифференцированию. Это действие называется интегрированием, а функция, восстановленная по производной, называется первообразной и обозначается F(x)+C
Совокупность F(x)+C всех первообразных функций 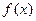
на промежутке (a; b) называется неопределённым интегралом от функции 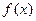 на этом промежутке:
на этом промежутке:  .
. 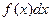 называется подынтегральным выражением;
называется подынтегральным выражением; 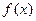 - подынтегральная функция; С - произвольная постоянная.
- подынтегральная функция; С - произвольная постоянная.
Свойства неопределённого интеграла.
1. Производная неопределённого интеграла равна подынтегральной функции; дифференциал неопределённого интеграла равен подынтегральному выражению:
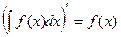 ;
; 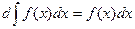
2. Неопределённый интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной.
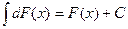
3. Постоянный множитель можно выносить за знак неопределённого интеграла:
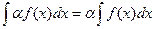
4. Неопределённый интеграл от суммы (разности) функций равен сумме (разности) неопределённых интегралов от каждой функции:
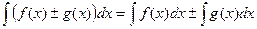
Основные формулы интегрирования
1. 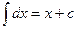
2. 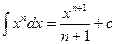
3. 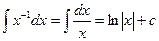
4. 
5. 
6. 
7. 
8. 
9. 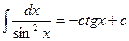
10. 
11. 
Методы интегрирования
Непосредственное интегрирование- это способ интегрирования, при котором данный интеграл путём тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам.
Пример1. Найти интеграл 

Решение: Преобразуем подынтегральную функцию, применяя свойства степени
 ;
; 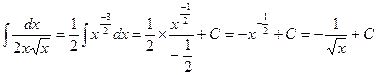
Пример 2. Найти интеграл 
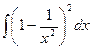 .
.
Решение: Раскроем по формуле (а-в)² =а² -2ав+в² скобки 
 . и разобьем интеграл согласно свойствам на сумму интегралов:
. и разобьем интеграл согласно свойствам на сумму интегралов: 

Интегрирование методом подстановки.
Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки.
Сущность этого метода заключается в том, что путём введения новой переменной удаётся свести данный интеграл к новому интегралу. Который сравнительно легко берётся непосредственно.
Для интегрирования методом подстановки можно использовать следующую схему:
1) Часть подынтегральной функции заменить новой переменной;
2) Найти дифференциал от обеих частей замены;
3) Всё подынтегральное выражение выразить через новую переменную(после чего должен получиться табличный интеграл);
4) Найти полученный табличный интеграл;
5) Сделать обратную замену.
Пример 3. Найти интеграл 
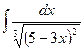 .
.
Решение Введём замену: 5-3x=t, тогда -3dx=dt, откуда  . Далее получаем
. Далее получаем 
Пример 4. Найти интеграл 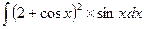
Решение. Введём замену 2+cosx=t, тогда –sinxdx=dt, откуда sinxdx=-dt. Далее получаем 
Определённый интеграл. Понятие определённого интеграла.
Пусть функция y=f(x)определена на отрезке  и на этом отрезке принимает только положительные значения. Разобьём этот отрезок на n равных частей, т.е. получим n равных отрезков, длина которого равна
и на этом отрезке принимает только положительные значения. Разобьём этот отрезок на n равных частей, т.е. получим n равных отрезков, длина которого равна 
В каждом отрезке произвольным образом выберем точку 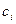 и составим сумму:
и составим сумму: 
 Эта сумма называется интегральной суммой.
Эта сумма называется интегральной суммой.
Геометрически каждое слагаемое
интегральной суммы равно площади
прямоугольника с основанием 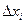
и высотой  , а вся сумма равна
, а вся сумма равна
площади ступенчатой фигуры. Будем
увеличивать число делений, сумма
будет стремиться к некоторому
конечному пределу независимо от
выбора
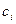 . Этот предел называется определённым интегралом от функции f(x) на отрезке
. Этот предел называется определённым интегралом от функции f(x) на отрезке  и обозначается:
и обозначается: 
Число а называется нижним пределом, число в - верхним пределом. Если f(x)> 0 на  , то
, то 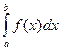 численно равен площади криволинейной трапеции аАВв, ограниченной прямыми х=а, х=в, т.е.
численно равен площади криволинейной трапеции аАВв, ограниченной прямыми х=а, х=в, т.е. 
Основные свойства определённого интеграла.
1.  , где
, где 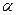 - любое действительное число.
- любое действительное число.
2. При перестановке пределов интегрирования знак интеграла меняется на противоположенный: 
3. Отрезок интегрирования можно разбить на части:  a< c< b
a< c< b
4. Постоянный множитель можно выносить за знак интеграла: 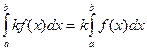
5. Интеграл от алгебраической суммы функций равен такой же алгебраической сумме интегралов от всех слагаемых: 
Методы вычисления определённого интеграла.
1. Непосредственное вычисление определённого интеграла. В этом случае
применяется формула Ньютона-Лейбница 
Пример 5. Вычислить интеграл 
Решение Применяем 5свойство и находим первообразную, по формуле Ньютона-Лейбница вычисляем определённый интеграл: 
Пример 6 Вычислить интеграл 
Решение Воспользуемся определением степени с дробными показателями, правилом деления суммы на число и вычислением определённого интеграла по формуле Ньютона-Лейбница 


2. Вычисление определённого интеграла методом подстановки.
Вычисление определённого интеграла методом подстановки состоит в следующем:
1) часть подынтегральной функции заменить новой переменной;
2) найти дифференциал от обеих частей замены;
3) найти новые пределы определённого интеграла;
4) все подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл);
5) вычислить полученный табличный интеграл.
Пример 7 Вычислить интеграл 
Решение Произведём замену 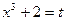 , тогда
, тогда 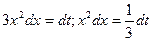 . Найдём новые границы интеграла
. Найдём новые границы интеграла  . Выразим подынтегральное выражение через t и dt и перейдём к новым границам интегрирования, получаем
. Выразим подынтегральное выражение через t и dt и перейдём к новым границам интегрирования, получаем 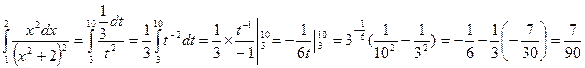
Пример 8 Вычислит интеграл 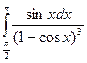
Решение: 1-cosx=t; sinxdx=dt;  ;
; 

Приложения определённого интеграла.
Понятие определённого интеграла широко применяется для вычисления различных геометрических и физических величин.
Площади плоских фигур.
Площадь криволинейной трапеции, ограниченной графиком непрерывной функции y=f(x), осью ОХ и двумя параллельными прямыми х=а и х=в, вычисляется по формуле  , если
, если 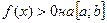 и
и  , если
, если 
Пример 9 Вычислить площадь фигуры, ограниченной кривой  и осью ох
и осью ох
Решение: Найдём границы интегрирования, т.е. абсциссы точек пересечения графиков функций  и у=0, для этого решим уравнение 6х-х² -5=0,
и у=0, для этого решим уравнение 6х-х² -5=0,
х² -6х+5=0, 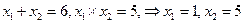
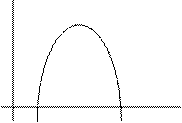 Найдём искомую площадь фигуры.
Найдём искомую площадь фигуры.
Площадь фигуры, ограниченной
двумя функциями 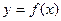 и
и  ,
,
изображёнными на рисунке вычисляются
по формуле 


 Пример 10 вычислить площадь фигуры, ограниченной линиями у=4-х² и у=х² -2х
Пример 10 вычислить площадь фигуры, ограниченной линиями у=4-х² и у=х² -2х
Решение Найдём точки пересечения
линий, для этого решим
систему 
Имеем 4-x² =x² -2x, 2x² -2x-4=0, x² -x-2=0

Искомую площадь
вычисляем по формуле: 
Объём тела вращения.
Объём тела, образованного вращением вокруг оси ОХ криволинейной трапеции, ограниченной непрерывной функцией 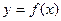 , осью ОХ, и двумя параллельными прямыми х=а, х=в
, осью ОХ, и двумя параллельными прямыми х=а, х=в
Вычисляется по формуле: 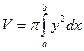
Пример 11. Вычислить объём тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболой y² =2x, прямой х=3 и осью ОХ.
Решение. Применяя формулу,
находим 
Объём тела, образованного вращением
вокруг оси ОУ криволинейной трапеции,
ограниченной непрерывной функцией
y=f(x), осью ОУ и двумя параллельными
прямыми у=а, у=в, вычисляется по формуле: 
Пример 12. Вычислить объём тела, образованного вращением вокруг оси ОУ фигуры, ограниченной параболой у=х² и прямой у=4
Решение. Применяя формулу,
находим 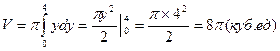
Нахождение пройденного пути. Если тело движется прямолинейно со скоростью V=V(t), то путь, пройденный телом за промежуток времени  вычисляется по формуле
вычисляется по формуле 
Пример 13. Тело движется прямолинейно со скоростью  .Вычислить путь, пройденный телом от начала движения до остановки.
.Вычислить путь, пройденный телом от начала движения до остановки.
Решение. Найдём момент времени, когда тело остановилось, т.е. решим уравнение  Следовательно тело остановилось через 4 секунды.
Следовательно тело остановилось через 4 секунды.
Путь, пройденный телом за это время, находится по формуле: 
Нахождение работы переменной силы. Если переменная сила F=F(x) действует в направлении оси ОХ, то работа силы на отрезке  вычисляется по формуле:
вычисляется по формуле: 
Пример 14 Вычислить работу, которую нужно совершить при сжатии пружины на 0, 08 м, если для её сжатия на 1см требуется сила 10 Н.
Решение. Согласно закону Гука, сила F, растягивающая или сжимающая пружину на х метров, равна F=kx, где k-коэффициент упругости пружины. Из условия следует 10=0, 01k т.е. k=1000. искомую работу находим по формуле: 
Пример 15 Для сжатия пружины на 3 см необходимо совершить работу в 16 Дж. На какую длину можно сжать пружину, совершив работу в 144 Дж?
Решение. По закону Гука F=kx, тогда 
Так ка