
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы математической статистики
|
|
(Е.П. Врублевский, О.Е. Лихачев, Л.Г. Врублевская)
Применяя в исследовании те или иные методы, в конечном итоге экспериментатор получает большую или меньшую совокупность различных числовых показателей, призванных характеризовать изучаемое явление. Но без систематизации и надлежащей обработки полученных результатов, без глубокого и всестороннего анализа фактов не удается извлечь заключенную в них информацию, открыть закономерности, сделать обоснованные выводы. Приведенные в тексте самые элементарные и вполне доступные для каждого студента приемы математической обработки результатов носят демонстрационный характер. Это означает, что примеры иллюстрируют применение того или иного математико-статистического метода, а не дают его развернутую интерпретацию.
Средние величины и показатели вариации. Прежде чем говорить о более существенных вещах, необходимо уяснить такие статистические понятия, как генеральная и выборочная совокупности. Группа чисел, объединяемых каким-либо признаком, называется совокупностью. Наблюдения, проводимые над какими-то объектами, могут охватывать всех членов изучаемой совокупности без исключения или ограничиваться обследованием лишь некоторой ее части. В первом случае наблюдение будет называться сплошным, или полным, во втором - частичным, или выборочным. Сплошное обследование проводится очень редко, так как в силу ряда причин оно практически либо невыполнимо, либо нецелесообразно. Так, невозможно, например, обследовать всех мастеров спорта по легкой атлетике. Поэтому в подавляющем большинстве случаев вместо сплошного наблюдения изучению подвергают какую-то часть обследуемой совокупности, по которой и судят о ее состоянии в целом.
Совокупность, из которой отбирается часть ее членов для совместного изучения, называется генеральной, а отобранная тем или иным способом часть данной совокупности получила название выборочнойсовокупности или просто выборкой. Следует уточнить, что понятие генеральной совокупности является относительным. В одном случае это все спортсмены, а в другом - города, вуза. Так, например, генеральной совокупностью могут быть все студенты вуза, а выборкой - студенты специализации футбола. Число объектов в любой совокупности называется объемом (объем генеральной совокупности обозначается N, а объем выборки n).
Предполагается, что выборка с должной достоверностью представляет генеральную совокупность только в том случае, если ее элементы избраны из генеральной нетенденциозно. Для этого существует несколько путей: отбор выборки в соответствии с таблицей случайных чисел, разделение генеральной совокупности на ряд непересекающихся групп, когда из каждой выбирается определенное количество объектов, и др.
Что касается объема выборки, то в соответствии с основными положениями математической статистики выборки тем представительнее (репрезентативнее), чем она полнее. Исследователь, стремясь к рентабельности своей работы, заинтересован в минимальном объеме выборки, и в такой ситуации количество объектов, отбираемых в выборку, является результатом компромиссного решения. Чтобы знать, насколько выборка достаточно достоверно представляет генеральную совокупность, необходимо определить ряд показателей (параметров).
Вычисление средней арифметической величины. Средняя арифметическая величина выборки  характеризует средний уровень значений изучаемой случайной величины в наблюдавшихся случаях и вычисляется путем деления суммы отдельных величин исследуемого признака на общее число наблюдений:
характеризует средний уровень значений изучаемой случайной величины в наблюдавшихся случаях и вычисляется путем деления суммы отдельных величин исследуемого признака на общее число наблюдений:
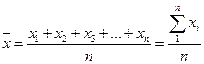 , (1)
, (1)
где х i - вариант ряда;
п -объем совокупности.
Суммой Σ принято обозначать суммирование тех данных, которые стоят справа от него. Нижние и верхние показатели Σ указывают, с какого числа следует начать сложение и какими показателями его закончить. Так,  обозначает, что необходимо сложить все х, имеющие порядковые номера от 1 до п. Знак
обозначает, что необходимо сложить все х, имеющие порядковые номера от 1 до п. Знак  показывает суммирование всех х от первого до последнего показателя.
показывает суммирование всех х от первого до последнего показателя.
Таким образом, вычисления по формуле (1) предполагают следующий порядок действий:
1. Суммируют все полученные хi, т. е.  ,
,
2. Найденную сумму  - делят на объем совокупности п.
- делят на объем совокупности п.
Для удобства и наглядности работы с показателями необходимо составить таблицу, так как сложению подлежат xi , перебираемые от первого до последнего числа.
Например, средняя арифметическая определяется по формуле:

Результаты измерений приведены в таблице 1.
Таблица 1
Результаты тестирования спортсменов
| № п/п | ∑ | ||||||||
| хi | 1, 25 | 1, 30 | 1, 32 | 1, 36 | 1, 38 | 1, 40 | 1, 42 | 1, 45 | 10, 88 |
Обратим внимание на то, что точность вычислений и точность измерений должны совпадать: если измеренные величины имеют точность до сотых, то и промежуточные вычисления и конечный результат должны быть представлены с точностью до сотых.
Таким образом, полученные показатели, представленные вариационным рядом, имеют типичную характерную для всего ряда величину  = 1, 36 (с).
= 1, 36 (с).
Среднее арифметическое дает возможность:
а) охарактеризовать исследуемую совокупность одним числом;
б) сравнить отдельные величины со средним арифметическим;
в) определить тенденцию развития какого-либо явления;
г) сравнить разные совокупности;
д) вычислить другие статистические показатели, так как многие статистические вычисления опираются на среднее арифметическое.
Однако одно только среднее арифметическое не дает возможности глубоко анализировать сущность того или иного явления и их взаимные различия.
Вычисление среднего квадратического (стандартного) отклонения. При анализе статистической совокупности одним из важных показателей является расположение значений элементов совокупности вокруг среднего значения (варьирование). Для характеристики варьирования в практике исследовательской работы рассчитывают среднее квадратическое отклонение (оно называется также стандартным отклонением и обозначается буквой S), которое отражает степень отклонения результатов от среднего значения, выражается в тех же единицах измерения. Для большинства исследователей привычно обозначать эту величину греческой буквой σ (сигма). На самом деле, в специальной литературе по статистике σ - стандартное отклонение в генеральной совокупности, a S - оценка этого параметра в исследованной выборке. Но чтобы не запутывать начинающих исследователей, будем обозначать стандартное отклонение знаком σ и вычислять по формуле:
 , (2)
, (2)
где 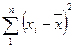 - сумма разности между каждым показателем и средней арифметической величиной (сумма квадратов отклонений);
- сумма разности между каждым показателем и средней арифметической величиной (сумма квадратов отклонений);
п - объем выборки (число измерений или испытуемых).
Если число измерений не более 30, т.е. n ≤ 30, используется формула:
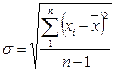 , (3)
, (3)
Необходимо подчеркнуть, что чем сильнее варьирует признак, тем больше величина этого показателя, и, наоборот, чем слабее он варьирует, тем меньше среднее квадратическое отклонение.
Для вычисления σ надо произвести следующие действия:
1. Определяют среднюю арифметическую  .
.
2. Из каждого варианта вычитают среднюю арифметическую: xi-  .
.
3. Найденную разность возводят в квадрат: (xi-  )2.
)2.

4. Определяют сумму всех квадратов разностей.
5. Найденную сумму делят на объем совокупности п.
Исходные данные заносятся в таблицу и последовательно выполняются перечисленные выше действия. Пример.
Таблица 2
Результаты вычислений средней арифметической
| № п/п | xi | xi- 
| (xi-  )2 )2
|
| 1, 25 | -0, 11 | 0, 0121 | |
| 1, 30 | -0, 06 | 0, 0036 | |
| 1, 32 | -0, 04 | 0, 0016 | |
| 1, 36 | 0, 00 | 0, 0000 | |
| 1, 38 | 0, 02 | 0, 0004 | |
| 1, 40 | 0, 04 | 0, 0016 | |
| 1, 42 | 0, 06 | 0, 0036 | |
| 1, 45 | 0, 09 | 0, 0081 | |
| ∑ | 10, 88 | - | 0, 031 |

В целом данные столбца 3 показывают, как все варианты рассеиваются относительно средней величины.
При определении среднего квадратического отклонения большое значение имеет столбец 3, в котором от каждого варианта вычитается значение средней арифметической. Таким образом, показатели столбца 3 указывают на то, как каждый конкретный вариант соотносится со средним значением. Если средняя величина определена верно, то сумма отрицательных величин по модулю должна быть равна сумме положительных величин.
Вычисляя среднюю арифметическую, группу исходных данных заменили одной величиной, самой типичной и характерной. Теперь необходимо заменить все показатели рассеивания одним показателем - средней арифметической всех показателей рассеивания. Однако при правильном исчислении средняя сумма отрицательных показателей должна быть равна сумме положительных показателей, т.е. при вычислении средней арифметической их сумма должна быть равна нулю. Поэтому предлагается возвести все знаковые показатели в квадрат, а потом найти среднюю арифметическую всех квадратов. Именно с этой целью в столбце 4 находятся квадраты разностей (х -  )2 с целью определения средней арифметической среди них.
)2 с целью определения средней арифметической среди них.
Таким образом, среднее квадратическое отклонение представляет собой среднюю арифметическую величину всех (xi-  )2. Эта величина указывает на рассеивание исходных данных относительно средней арифметической (в квадрате).
)2. Эта величина указывает на рассеивание исходных данных относительно средней арифметической (в квадрате).
Обратим внимание также на то, что вычисления среднего квадратического отклонения следует рассчитывать с большей точностью. При нахождении среднего квадратического отклонения, извлекая корень, мы возвращаемся к исходной точности.
Чем меньше величина σ, тем плотнее результаты около средней, что может говорить как о стабильности показателей одного испытуемого, так и о ровности результатов группы или одинаковой подготовленности спортсменов.
Существует и более простой способ вычисления стандартного отклонения по следующей формуле:
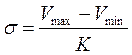 , (4)
, (4)
где Vmax - наибольшее значение показателя;
Vmin - наименьшее значение показателя;
К - табличный коэффициент (табл. 3), обусловленный объемом выборки (n).
Математическими исследованиями установлено, что при обоих методах расчета имеются вполне удовлетворительные совпадения величин. Кроме того, вычислить σ по размаху выгодно при малом числе измерений (не более 20) (Таблица 3).
Таблица 3
Коэффициенты (К) для вычисления среднего квадратического отклонения по амплитуде вариационного ряда
| 1, 13 | 1, 69 | 2, 06 | 2, 33 | 2, 53 | 2, 70 | 2, 85 | 2, 97 | |||
| 3, 08 | 3, 17 | 3, 26 | 3, 34 | 3, 41 | 3, 47 | 3, 53 | 3, 59 | 3, 64 | 3, 69 | |
| 3, 74 | 3, 78 | 3, 82 | 3, 86 | 3, 90 | 3, 93 | 3, 96 | 4, 00 | 4, 03 | 4, 09 |
Следует иметь в виду, что подавляющее большинство признаков в однородной группе подчиняется закону так называемого нормального распределения.Это значит, что максимальная частота встречаемости признака находится около средней арифметической величины. Чем больше величины отклоняются от  в ту или другую сторону, тем реже встречаются. В зависимости от величины σ форма нормальной кривой может быть пологой (при большой величине σ) и более или менее крутой (при небольшой величине σ). Во всех случаях нормальная кривая строго симметрична относительно центра распределения и сохраняет правильную колоколообразную форму. Для того чтобы убедиться в том, что распределение близко к нормальному, необходимо сопоставить значения средней арифметической, моды и медианы. Если данные показатели приблизительно совпадают, то распределение можно считать нормальным.
в ту или другую сторону, тем реже встречаются. В зависимости от величины σ форма нормальной кривой может быть пологой (при большой величине σ) и более или менее крутой (при небольшой величине σ). Во всех случаях нормальная кривая строго симметрична относительно центра распределения и сохраняет правильную колоколообразную форму. Для того чтобы убедиться в том, что распределение близко к нормальному, необходимо сопоставить значения средней арифметической, моды и медианы. Если данные показатели приблизительно совпадают, то распределение можно считать нормальным.
При нормальном распределении варианты расположены в определенных границах. Так, в пределах  расположено 99, 7% всех результатов измерений.
расположено 99, 7% всех результатов измерений.
В практике спортивных исследований часто возникают затруднения, связанные с тем, что один или несколько показателей оказываются резко отличающимися от остальных. В таких случаях при исключении сильно отклоняющихся «ошибочных» результатов измерений используется «Правило трех сигм». Производится это следующим образом: 1) вычисляется  и σ без варианта, который резко отличается от остальных; 2) вычисляется величина
и σ без варианта, который резко отличается от остальных; 2) вычисляется величина  ; 3) если сомнительный вариант выходит за пределы
; 3) если сомнительный вариант выходит за пределы  , его исключают из дальнейших расчетов.
, его исключают из дальнейших расчетов.
Пример.При измерении угла в коленном суставе ноги, стоящей на задней колодке, в стартовом положении у 20 спортсменов получили величины от 100 до 140°. При этом только одно измерение составило 140°, а остальные - от 100° до 120°. Следует ли измерение 140° исключить из дальнейших расчетов?
По известным формулам проводим расчет  и σ (при этом сомнительный вариант 140° не учитываем!). Получаем
и σ (при этом сомнительный вариант 140° не учитываем!). Получаем  = 111º σ = 7, 3°, 3σ = 3 ∙ 7, 3° = 22°. Следовательно, вариант 140° не должен выходить за пределы от 111º - 22° = 89° до 111º + + 22°=133°. Поскольку он больше верхнего предела 133°, его следует исключить из дальнейших расчетов.
= 111º σ = 7, 3°, 3σ = 3 ∙ 7, 3° = 22°. Следовательно, вариант 140° не должен выходить за пределы от 111º - 22° = 89° до 111º + + 22°=133°. Поскольку он больше верхнего предела 133°, его следует исключить из дальнейших расчетов.
Вычисление коэффициента вариации. Как уже отмечалось, σ выражается в тех же единицах, что и характеризуемый его признак. Поэтому, когда возникает необходимость сравнивать изменчивость признаков, выраженных разными единицами, приходится пользоваться относительными показателями вариации. Одним из таких показателей является коэффициент вариации (V).Этот показатель определяется как отношение среднего квадратического отклонения к среднему арифметическому, выраженное в процентах. Вычисляется он по формуле:
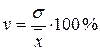 , (5)
, (5)
По формуле находим значение коэффициента вариации, определяющего, какой процент от средней арифметической составляет показатель рассеивания.

Это означает, что рассеивание показателей относительно средней арифметической составляет 1, 54 %.
В практике физической культуры и спорта не существует такого критерия, однако сам коэффициент вариации часто употребляется и отражает рассеивания группы весьма характерно. Так, например, коэффициент вариации может указать на квалификацию испытуемого. Известно, что высококвалифицированные спортсмены показывают очень близкие результаты, т. е. рассеивание их данных незначительно и коэффициент вариации должен быть невысоким, в то время как показатели спортсменов невысокой квалификации сильно разнятся, поэтому их коэффициенты вариации должны быть выше.
Пример. Рассмотрим результаты забега (с) на 200 м десяти юношей. Данные приведены в таблице. Определим среднюю арифметическую, среднее квадратическое отклонение и коэффициент вариации:



Таблица 4
Результаты забега юношей
| № п/п | xi | xi- 
| (xi-  )2 )2
|
| 28, 0 28, 5 27, 8 27, 4 27, 0 26, 8 | 0, 4 0, 9 0, 2 -0, 2 -0, 5 -0, 8 | 0, 16 0, 81 0, 04 0, 04 0, 25 0, 64 | |
| ∑ | 165, 5 | - | 1, 94 |
Теперь рассмотрим результаты спортсменов высокого класса.
Таблица 5
Результаты забега спортсменов высокого класса
| № п/п | yi | yi- 
| (yi-  )2 )2
|
| 21, 0 21, 2 21, 3 21, 4 21, 6 21, 7 | -0, 36 -0, 16 0, 06 0, 04 0, 24 0, 34 | 0, 1296 0, 0256 0, 0036 0, 0016 0, 0576 0, 1156 | |
| Всего | 128, 2 | - | 0, 3327 |
Определим среднюю арифметическую, дисперсию, среднее квадратическое отклонение и коэффициент вариации:


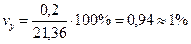
Итак, проанализировав результаты спортсменов при помощи коэффициента вариации и среднего квадратического отклонения, можно сделать вывод, что рассеивание исходных данных у них значительно меньше, а значит, и квалификация спортсменов выше.
Коэффициент вариации выражается относительным числом в процентах. Это создает возможность сравнения показателей с различными наименованиями.
В статистике принято среднюю арифметическую относить к мерам центральной тенденции, а среднее квадратическое отклонение и коэффициент вариации - к мерам вариабельности.
По аналогии с биологическими исследованиями принято считать, что группа показателей, коэффициент вариации которых не превышает 10-15%, представляет собой стабильные измерения, мало отличающиеся друг от друга. Если же V больше, то группа неоднородна.
Следует учитывать, что в спортивных исследованиях применение интервала 10-15% для определения однородности показателей является весьма условным и зависит от того, какие объекты исследуются. Не надо проводит специальных расчетов, чтобы убедиться, например, в существовании различий между результатами спортсменов высших и низших разрядов. Понятно, что результаты спортсменов высших разрядов должны быть более однородны и стабильны, чем результаты спортсменов низших разрядов. Следовательно, в первом случае коэффициент вариации должен быть значительно ниже, чем во втором.
Вычисление стандартной ошибки средней арифметической. Как правило, выборочные характеристики не совпадают по абсолютной величине с соответствующими генеральными параметрами, поскольку, какой бы репрезентативной ни была выборка, ее объем меньше генеральной совокупности. Величина отклонения выборочной средней от ее генерального параметра называется статистической стандартной ошибкой выборочного среднего арифметического или ошибкой репрезентативности. Иногда этот показатель называется просто ошибкой средней. Следует иметь в виду, что статистическая «ошибка» - это не ошибка, допускаемая при измерении объектов педагогики. Возникает она исключительно в процессе отбора варианта из генеральной совокупности и к ошибкам измерений отношения не имеет. Этот показатель (обычно он обозначается символом т) характеризует меру представительности данной выборки в генеральной совокупности. Иными словами, ошибка указывает на величину различия между средними арифметическими - генеральной и выборочной совокупностями. Определить ошибку средней арифметической можно двумя способами.
1. Если выборочная совокупность составлена таким образом, что любой объект генеральной может попасть в выборку несколько раз, то ошибка средней арифметической определяется по формуле:
 , (6)
, (6)
где σ - среднее квадратическое отклонение выбор очной совокупности;
п - объем выборки (число измерений или испытуемых).
Более точной является формула:
 , (7)
, (7)
При объемах выборки n ≥ 30 различие между n и (n - 1) практически не ощущается, вследствие чего можно пользоваться любой из формул - (6) и (7). При выборках численностью менее 30 такое различие более ощутимо, и в этом случае предпочтительна формула (7).
2. Если выборка образована из генеральной таким образом, что любой объект генеральной совокупности не может быть в ней повторим, ошибка может быть определена по формуле:
 , (8)
, (8)
где σ - среднее квадратическое отклонение выборочной совокупности;
п - объем выборки;
N - объем генеральной совокупности.
Совершенно очевидно, что, пользуясь формулой (8), необходимо знать численность генеральной совокупности N, без чего можно обойтись в формулах (6) и (7). Отсюда следует, что если численность генеральной неизвестна, как это характерно для работ на материале спорта, нужно пользоваться формулами (6) и (7).
Например, в приведенном ранее примере определялся угол в коленном суставе ноги, стоящей на задней стартовой колодке, у 20 спортсменов и была получена  , равная 111º. А в какой мере эта величина будет показательна, если исследовать несколько сотен спортсменов? Ответ на этот вопрос и даст значение стандартной ошибки средней арифметической, которая определяется по формуле (7):
, равная 111º. А в какой мере эта величина будет показательна, если исследовать несколько сотен спортсменов? Ответ на этот вопрос и даст значение стандартной ошибки средней арифметической, которая определяется по формуле (7):
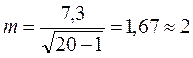
Следовательно,  ± т = 111±2°. Это обозначает, что полученная средняя арифметическая величина
± т = 111±2°. Это обозначает, что полученная средняя арифметическая величина  =111° в других аналогичных исследованиях может иметь значения 109° (111-2=109) до 113° (111+2=113).
=111° в других аналогичных исследованиях может иметь значения 109° (111-2=109) до 113° (111+2=113).
Как рассчитывать т, если известна генеральная совокупность, покажем на примере.
Пример. В школе 730 мальчиков 14 лет. Из них у группы школьников двух классов (n=50) фиксировалось количество приседаний за 20 с. Определено:  = 13, 0 раз, σ = 2, 2. В соответствии с формулой (8) определяем величину ошибки средней арифметической для 50 школьников:
= 13, 0 раз, σ = 2, 2. В соответствии с формулой (8) определяем величину ошибки средней арифметической для 50 школьников:

Найденное значение (т = 0, 3) свидетельствует, что величину средней арифметической генеральной совокупности (730 школьников) так же, как и у 50 школьников, можно принять за 13, 0 раз. При этом погрешность такого предположения составит 0, 3 приседания.
Таким образом, можно заключить, что при увеличении числа испытуемых m будет уменьшаться и стремиться к 0.
Взаимосвязь результатов исследования. Вматематике существует две формы взаимосвязи процессов или явлений. Функциональная связь отражает такое взаимное влияние признаков, когда одному значению какого-либо признака точно соответствует одно определенное значение другого признака. Например, повышение t° на 10° ускоряет химическую реакцию в два раза, площадь круга равняется квадрату его радиуса, умноженному на константу р, и т.д. Такого рода связи встречаются в точных науках (физике, геометрии и др.) и очень редко в физической культуре и спорте. Здесь наиболее часто наблюдается взаимная связь между признаками, когда значению одного признака соответствует множество значений другого. Подобная взаимосвязь называется корреляционной связью или корреляцией. Если такая связь велика, говорят, что признаки тесно (или сильно) коррелируют, в противном случае - они слабо коррелируют. Мерой зависимости (теснотой связи) между признаками является коэффициент корреляции, а его вычисление - корреляционным анализом.
По своему характеру корреляция бывает прямой (положительной) и обратной (отрицательной). Прямая корреляция отражает однотипность в изменении признаков: с увеличением значений первого признака увеличивается значение и другого, или с уменьшением первого - уменьшается второй. Например, повышение силовых возможностей мышц нижних конечностей сказывается на росте результата в тройном прыжке с места, а улучшение (уменьшение времени) результата в беге на 30 м с ходу приводит к улучшению (снижению времени) в беге на 100 м со старта. Обратная корреляция указывает на увеличение первого признака при уменьшении второго, или уменьшение первого признака при увеличении второго. Например, повышение силовых показателей мышц нижних конечностей приводит к снижению времени (улучшению) результата в беге на 100 м, а уменьшение времени опоры и полета сказывается на увеличении скорости бега. В студенческой среде бытует ошибочное логическое представление, что положительная корреляция - это хорошо, а отрицательная - плохо. Как видим, знак коэффициента корреляции отражает направленность зависимости между показателями, а абсолютное значение коэффициента (от 0 до 1) оценивает количественную меру связи.
Существует три способа выражения корреляции: корреляционный график; корреляционное поле и коэффициент корреляции.
По сравнению с численными значениями графики не несут в себе никакой новой информации, их отличительная черта - наглядность. В самом деле, если данные наблюдений нанести на график, то по нему можно определить, есть ли корреляция и какова ее характеристика.
В целом по графику можно определить следующие моменты:
- если экспериментальные точки рассеяны по полю графика хаотично и по ним невозможно провести линию, то корреляция отсутствует;
- если точки группируются вдоль какой-либо линии, то корреляция есть, и она тем теснее, чем плотнее располагаются эти точки;
- по направлению линии, вдоль которой группируются точки, можно определить вид корреляции (положительная или отрицательная).
Виды корреляционных связей между измеренными признаками могут быть различны: так, корреляция бывает линейной и нелинейной, положительной и отрицательной. Она линейна - если с увеличением или уменьшением одной переменной X, вторая переменная Y в среднем либо также растет, либо убывает. Она нелинейна, если при увеличении одной величины характер изменения второй не линеен, а описывается другими законами.
Корреляция будет положительной, если с увеличением переменной X переменная Y в среднем также увеличивается, а если с увеличением X переменная Y имеет в среднем тенденцию к уменьшению, то говорят о наличии отрицательной корреляции. Возможна ситуация, когда между переменными невозможно установить какую-либо зависимость. В этом случае говорят об отсутствии корреляционной связи. Подчеркнем, однако, что нередко встречаются задачи, в которых традиционная и наиболее часто встречающаяся в исследованиях линейная корреляционная связь отсутствует, в то время как имеется высокозначимая криволинейная связь, например, полиномиальная или гиперболическая.


 у у
у у

 |
х х
 | |||
 | |||
Рис.1. Прямая корреляционная связьРис.2. Обратная связь
Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.
Корреляционное поле представляет собой таблицу, отражающую масштаб обоих признаков хi и уi. В клеточки таблицы вписывается количество точек, соответствующее экспериментальным.
Корреляционное поле показывает следующие моменты:
- если точки рассеяны по полю бессистемно, хаотично и окаймляющая их кривая приближается к виду окружности, то корреляции между признаками нет;
- если окаймляющая кривая вытянута, т.е. приближается по виду к линии, то корреляция есть;
- если площадь вытянута и напоминает кривую, т. е. корреляция есть, и по наклону этой предполагаемой кривой, соотнеся ее с возрастанием или убыванием масштаба, можно определить вид корреляции (положительная или отрицательная).
 а а


| Сильная положительная линейная корреляционная зависимость |    б б
| Сильная отрицательная линейная корреляционная зависимость | ||||||||||
в
| Отсутствие статистической зависимости |    г г
| Сильная нелинейная статистическая зависимость |
Рис.3. Корреляционное поле
На рисунке (а) окаймляющая кривая вытянута, приближается по виду к линии, наклон которой отражает возрастание как первого хi, так и второго признака уi. Следовательно, в этом случае имеет место корреляция положительная.
На следующем рисунке (б) показана корреляционная связь, отражающая отрицательную корреляцию, так как наклон предполагаемой кривой указывает на увеличение признака хi при уменьшении признака уi.
Третий рисунок (в) отражает отсутствие связи, четвертый (г) представляет нелинейную корреляционную связь.
Самым точным выражением корреляции является ее оценка при помощи специальных коэффициентов корреляции: 1) коэффициента корреляции в случае прямолинейной связи и 2) корреляционных отношений, если корреляция криволинейная.
Таким образом, перед вычислением коэффициента корреляции следует оценить с помощью корреляционного поля форму статистической взаимосвязи. Сделав это, на защите работы на вопрос: «Выбирая данный коэффициент корреляции, учитывали ли Вы форму зависимости и как Вы это делали?» Вы можете ответить: «Мы проводили визуальный анализ корреляционного поля». Дальше без комментариев.
Вычисление линейного коэффициента корреляции. Для оценки взаимосвязи, когда форма зависимости линейная, используется парный коэффициент корреляции Бравэ-Пирсона. Обозначается он латинской буквой r, и вычисляют его чаще всего по формуле:
 , (9)
, (9)
где rxy - коэффициент корреляции между признаками х и у; хi и уi - значения наблюдаемых величин х и у;  и
и  - средние арифметические значения признаков х и у;
- средние арифметические значения признаков х и у;
п - объем совокупности.
Коэффициент корреляции не должен превышать единицу.
Таким образом, - 1 < rxy < 1.
Если принять во внимание абсолютное значение rxy, т.е. без учета знака, его возможные значения могут быть заключены в интервале 0 < | rxy| < 1. Этот интервал позволяет исследователю ориентироваться по тесноте взаимосвязи: чем ближе расчетный коэффициент к единице, тем теснее коррелируют признаки; чем ближе к нулю, тем меньше взаимосвязь.
В практике ФКС условно приняты следующие интервалы:
1) 0, 99 < r < 0, 9 – очень сильная взаимосвязь;
2) 0, 89-0, 7 – сильная;
3) 0, 69-0, 5 – заметная;
4) 0, 49-0, 3 – умеренная;
5) 0, 29-0, 1 – слабая;
6) 0, 09-0 – нет взаимосвязи.
Кроме того, при расчете взаимосвязи и оценке показателей спортсменов высокой квалификации тренировочных воздействий тесная корреляция может быть равной 0, 85 и выше. По знаку коэффициента корреляции определяется, какова корреляция - положительная или отрицательная.
Коэффициент корреляции может быть вычислен и по следующей формуле:
 , (10)
, (10)
Пример. Оцените по данным, приведенным в таблице, взаимосвязь силы удара при броске мяча в гандболе хi (Н) и дальностью полета мяча уi ( м ).
1. Вычисляем  и
и  . Суммы столбцов 2 и 3 разделим на n = 6.
. Суммы столбцов 2 и 3 разделим на n = 6.


2. Вычисляем в столбце 4 отклонения отдельных результатов от средней  , (
, ( ), а в столбце 5 отклонения отдельных результатов от средней
), а в столбце 5 отклонения отдельных результатов от средней  , (
, ( ).
).
3. Вычисляем произведение отклонений ( )∙ (
)∙ ( ) в столбце 6 и находим сумму этих произведений ∑ (
) в столбце 6 и находим сумму этих произведений ∑ ( )∙ (
)∙ ( ) = 8, 55.
) = 8, 55.
4. В столбце 7 и 8 вычисляем квадраты отклонений ( )2 и (
)2 и ( )2 соответственно и находим суммы этих квадратов.
)2 соответственно и находим суммы этих квадратов.
5. Вычисляем rxy по формуле (9), подставив полученные значения в столбцах 6, 7, 8.

Таблица 6
Взаимосвязь силы удара и дальности полета мяча
| № п/п | хi | уi | хi - 
| уi - 
| (хi -  )(уi- )(уi-  ) )
| (хi -  )2 )2
| (уi-  )2 )2
|
| 10, 12 10, 30 10, 65 11, 00 11, 90 12, 30 | 25, 2 26, 4 27, 2 27, 9 28, 5 31, 2 | -0, 92 -0, 74 -0, 39 -0, 04 0, 86 1, 26 | -2, 5 -1, 3 -0, 5 0, 2 0, 8 3, 5 | 2, 30 0, 96 0, 19 0, 00 0, 69 4, 41 | 0, 85 0, 55 0, 15 0, 00 0, 74 1, 59 | 6, 25 1, 69 0, 25 0, 04 0, 64 12, 25 | |
| ∑ | 66, 27 | 166, 4 | - | - | 8, 55 | 3, 88 | 21, 12 |
Обратим внимание на знак полученного коэффициента. Знаменатель формулы дает всегда положительное число, а числитель зависит от знака произведения (хi -  )∙ (уi -
)∙ (уi -  ).В данном случае этот знак положительный (+8, 55), поэтому знак коэффициента корреляции тоже положительный.
).В данном случае этот знак положительный (+8, 55), поэтому знак коэффициента корреляции тоже положительный.
Итак, в примере коэффициент корреляции rxy= 0, 94.
Статистические выводы: 1) в связи с тем, что rxy = 0, 94 > 0, корреляция между признаками х и у имеет место; 2) так как значение rxy= 0, 94 близко к верхнему пределу интервала 0 < | rxy | < 1, то связь является очень тесной; 3) поскольку знак коэффициента положительный, корреляция является прямой: с увеличением первого признака х второй признак у также увеличивается.
Педагогический вывод. Дальность полета мяча у испытуемых существенно зависит от силы броска.
Этот коэффициент получил повсеместное распространение в спортивных исследованиях, в частности в практике ФКС он применяется во всех корреляционных расчетах.
При вычислении линейного коэффициента корреляции Бравэ-Пирсона следует учесть, что выводы дают корректные результаты в том случае, когда признаки распределены нормально и когда рассматривается взаимосвязь между большим количеством признаков. Для получения коэффициентов корреляции, свободных от значительных случайных ошибок, нужно не менее нескольких десятков измерений. В нашем примере при шести испытуемых вероятность ошибок очень велика. Напоминаем, что примеры в данном пособии носят характер иллюстрации методов, а не подробного изложения каких-либо научных экспериментов.
Для полноты информации на основании коэффициента корреляции определяют коэффициент детерминации D, который вычисляется по формуле:
 , (11)
, (11)
Этот коэффициент показывает часть общей вариации одного показателя, которая объясняется вариацией другого показателя. Так, например, если определен коэффициент корреляции между результатом в прыжках в длину и бегом на 30 м, равный - 0, 777, то коэффициент детерминации будет равен:
D = (-0, 777)2∙ 100% = 60, 3%
Следовательно, можно предполагать, что 60, 3 % взаимосвязи спортивного результата в прыжках в длину и в беге на 30 м объясняется их взаимовлиянием. Остальная часть (100% - 60, 3 %=39, 7%) вариации объясняется влиянием других неучтенных факторов. Таким образом, Вы можете рассчитать «свои» коэффициенты детерминации и интерпретировать их по аналогии с вышеописанным.
Вычисление рангового коэффициента корреляции. Внекоторых случаях невозможно определить количественные значения признаков. Например, невозможно определить комплексную характеристику ведения боя у фехтовальщиков, однако можно установить последовательность в оценке фехтовальщиков, исходя из количества выигранных боев. Этот же пример можно отнести к гимнастам, борцам, игровикам и т.д. В таких случаях применяется ранговый коэффициент корреляции. Наименование корреляции «ранговая» связано с понятием «ранг», т.е. имеющий порядковый номер. Кроме того, ранговый коэффициент корреляции позволяет измерить степень сопряженности между признаками независимо от закона распределения. Поэтому он используется для быстрой оценки взаимосвязи, когда показатели или признаки не могут быть измерены точно, но могут быть ранжированы.
Во всех этих случаях корреляционную связь между признаками можно оценить при помощи рангового коэффициента корреляции Спирмена (обозначается греческой ρ («ро»). Его вычисляют по формуле:
 , (12)
, (12)
гдеd = dx - dy - разность рангов данной пары показателей х и у, n - объем выборки.
Ранговый коэффициент имеет те же свойства, что и коэффициент Пирсона, и поэтому статистические выводы соответствуют статистическим выводам коэффициента Пирсона.
Пример 1. При выполнении программ одиночного катания места среди фигуристов распределились по порядку в обязательных хz и произвольных уz упражнениях. Существует ли связь между распределением мест в произвольных и обязательных упражнениях?
Исходные данные и основные расчеты приведены в таблице 7.
Таблица 7
Взаимосвязь распределения произвольных и обязательных упражнений
| № п/п | ∑ | |||||||
| хz (dx) | - | |||||||
| уz (dу) | - | |||||||
| dx – dу | -1 | -1 | -1 | - | ||||
| (dx – dу)2 |
1. Проранжируем (упорядочим и присвоим порядковые номера) показатели х и у (строки 2 и 3), в строки 2 и 3 заносим соответствующие испытуемым ранги по тому или иному показателю.
2. Вычисляем разность рангов dx – dу в строке 4.
3. Вычисляем квадраты разности рангов (dx – dу)2 и определяем их сумму в строке 5.
4. Вычисляем ρ, подставив полученные значения в формулу (12):

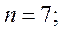
Полученный коэффициент ранговой корреляции ρ = 0, 86 свидетельствует о тесной взаимосвязи. Статистический вывод. Поскольку ρ = 0, 86, то связь между признаками есть, она - тесная, положительная.
Педагогический вывод.У наблюдаемых спортсменов отмечается тесная связь между выполняемыми произвольными и обязательными упражнениями.
Расположение исходных данных по рангу можно осуществить и тогда, когда они выражены в абсолютных числах. В этом случае, оценивая величины их показателей, назначают им ранги.
Рассмотрим пример, в котором ранги назначаются на основании расположения по порядку абсолютных величин.
Пример 2. Время отталкивания гандболиста при броске мяча хi (с); результативность броска мяча вворота - уi (% за игру).
Оцените, существует ли связь между этими показателями у восьми спортсменов. Исходные данные и основные расчеты приведены в таблице 8.
Таблица 8
Взаимосвязь между временем отталкивания при броске и результативностью попадания мяча в ворота
| № п/п | хi | уi | dx | dу | dx – dу | (dx – dу)2 |
| 0, 18 | 24, 2 | 1, 5 | -6, 5 | 42, 25 | ||
| 0, 18 | 24, 9 | 1, 5 | -5, 5 | 30, 25 | ||
| 0, 17 | 25, 6 | -3, 0 | 9, 00 | |||
| 0, 16 | 26, 7 | -1, 0 | 1, 00 | |||
| 0, 15 | 27, 8 | 5, 5 | 1, 5 | 2, 25 | ||
| 0, 15 | 28, 4 | 5, 5 | 2, 5 | 6, 25 | ||
| 0, 14 | 29, 9 | 5, 0 | 25, 00 | |||
| 0, 13 | 30, 5 | 7, 0 | 49, 00 | |||
| Всего | - | - | - | - | - | 165, 00 |
Напомним, что, как и в случае с критериями согласия, в выборочном методе равным значениям наблюдаемых величин присваиваются одинаковые ранги. С этой целью соответствующие ранги делятся между ними поровну.
Так, признак хi содержит первые два одинаковых значения, равные 0, 18, поэтому места между ними делятся поровну:  . Если значения были бы неодинаковыми, то они заняли бы I и II порядковые места. Показатель 0, 17 занимает следующее после них III место. На IV месте - показатель 0, 16; на V и VI - два одинаковых значения 0, 15, которые имеют ранг 5, 5, т.е.
. Если значения были бы неодинаковыми, то они заняли бы I и II порядковые места. Показатель 0, 17 занимает следующее после них III место. На IV месте - показатель 0, 16; на V и VI - два одинаковых значения 0, 15, которые имеют ранг 5, 5, т.е.  , и т.д.
, и т.д.
Аналогичным образом назначаем ранги признаку уi. Учитывая, что в первом случае (т.е. у признака хi) ранги назначались от большего числа к меньшему (от 0, 18 к 0, 13), тот же принцип соблюдается и для признака у, - наименьший ранг (I место) следует назначить наибольшему числу, равному 30, 5.
Остальные вычисления производятся так же, как и в примере 1. Ранговый коэффициент

Статистический вывод. Между рассмотренными признаками хi и уi существует тесная корреляционная связь обратного вида.
Педагогический вывод.У испытуемых наблюдается закономерность: чем быстрее они отталкиваются при броске (меньшее время отталкивания), тем точнее они попадают в ворота.
Поскольку в основу вычисления рангового коэффициента корреляции положены значения последовательности расположения объектов, а не собственно значения объектов, то теснота связи определяется слабее и точность исследований снижается, однако возрастает скорость обработки информации.
Следует подчеркнуть, что вычисление рангового коэффициента корреляции рекомендуется проводить в том случае, когда связанных пар больше пяти и когда достаточно получить лишь приблизительную информацию. В тех случаях, когда признаки поддаются количественному учету и есть основание считать, что их распределение подчинено нормальному закону распределения, преимущество должно оставаться за параметрическим коэффициентом Пирсона, как более мощным и надежным в практической работе.
Степень достоверности статистических показателей. В практике исследовательской работы решение той или иной задачи не обходится без сравнения. Сравнивать приходится данные контрольной и экспериментальной групп, показатели спортсменов до и после серии тренировок, различные меняющиеся с возрастом характеристики физической подготовленности и развития у школьников за несколько лет и т.д. Во всех этих и подобных случаях наличие существенного различия между параметрами совокупностей укажет на принципиальное отличие в группах по рассматриваемому признаку.
Чтобы решать вопрос об истинной значимости различий, наблюдаемых между выборочными средними, исходят из статистических гипотез - предположений или допущений о неизвестных генеральных параметрах, которые могут быть проверены на основании выборочных показателей. Поскольку в науке результаты исследований и вытекающие из них выводы никогда не принимаются со 100%-й уверенностью, т.е. всегда имеется некоторый риск в интерпретации результатов, который связан с существованием каких-то случайных причин. Экспериментатор может выбрать уровень значимости (обозначается р или α) - значение вероятности, при котором различия, наблюдаемые между выборочными показателями, можно считать несущественными, случайными. Самыми распространенными уровнями значимости в спортивных исследованиях являются 0, 05 и 0, 01, каждому из которых соответствует определенное значение надежности или доверительной вероятности (Р), а именно 0, 95 (95%) и 0, 99 (99%). Уровень значимости 0, 05 указывает на то, что в силу случайности возможна ошибка в 5%случаев, т.е. не чаще, чем 5 раз в 100 наблюдениях. Если нужна большая доказательность (достоверность) результатов, то уровень значимости должен быть повышен до 0, 01. Чем цифра меньше, тем уровень значимости, а следовательно, и достоверность результатов (степень доверия) выше. При уровне значимости 0, 01 вывод не обоснован только в одном случае из 100.
Оценку статистической достоверности производят при помощи специальных методов - критериев значимости. Следует знать, что критерии бывают параметрические (Стьюдента, Фишера) и непараметрические (Уайта, Вилкоксона, Ван дер Вардена и др.). Первые применимы («работают») лишь в тех случаях, когда генеральная совокупность, из которой взята выборка, распределяется нормально, а параметры сравниваемых групп равны между собой (σ 1 =σ 2). В действительности же эти условия выполняются не всегда, и в таких случаях корректнее применять непараметрические критерии, где оценка на достоверность связана с ранжированием исходных данных. В студенческих работах (и не только в них) на это часто закрывают глаза и используют во всех случаях только t-критерий Стьюдента. Кроме того, следует учитывать, что часто пытаются с помощью одной и той же формулы найти достоверность различий как между двумя независимыми группами (контрольной и экспериментальной), так и при определении изменений, происходящих с течением времени, когда сравнивают данные, зарегистрированные на той же группе «до» и «после», не учитывая, что выборки в этом случае коррелированы.
Статистическая достоверность имеет существенное значение в расчетной практике физической культуры и спорта. Ранее было отмечено, что из одной и той же генеральной совокупности может быть избрано множество выборок:
- если они подобраны корректно, то их средние показатели и показатели генеральной совокупности незначительно отличаются друг от друга величиной ошибки репрезентативности с учетом принятой надежности;
- если они избираются из разных генеральных совокупностей, различие между ними оказывается существенным. В статистике повсеместно рассматривается сравнение выборок;
- если они отличаются несущественно, непринципиально, незначительно, т.е. фактически принадлежат одной и той же генеральной совокупности, различие между ними называется статистически недостоверным.
Статистически достоверным различием выборок называется выборка, которая различается значимо и принципиально, т.е. принадлежит разным генеральным совокупностям.
В физической культуре и спорте оценка статистической достоверности различий выборок означает решение множества практических задач. Например, введение новых методик обучения, программ, комплексов упражнений, тестов, контрольных упражнений связано с их экспериментальной проверкой, которая должна показать, что испытуемая группа принципиально отлична от контрольной. Поэтому применяют специальные статистические методы, называемые критериями статистической достоверности, позволяющие обнаружить наличие или отсутствие статистически достоверного различия между выборками.
Оценка достоверности различий средних несвязанных (независимых) выборок. В большинстве исследований по спорту могут решаться задачи на выявление эффективности той или иной методики обучения и тренировки с применением определенных средств, приемов и способов организации занятий. Решение подобных задач осуществляется путем проведения сравнительного эксперимента с выделением различных групп, результаты которых в теории статистики принято называть независимыми (несвязанными). В практике спорта в таких случаях наиболее востребованным является t-критерий Стьюдента.
Критерий Стьюдента назван в честь английского ученого К. Госсета (Стьюдент - псевдоним), открывшего данный метод. Критерий Стьюдента является параметрическим, используется для сравнения абсолютных показателей выборок. Выборки могут быть различными по объему. Критерий Стьюдента определяется следующим образом:
1. Находим критерий Стьюдента t по формуле:
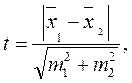 (13)
(13)
где  ,
,  - средние арифметические сравниваемых выборок;
- средние арифметические сравниваемых выборок;
т 1, m 2 – ошибки репрезентативности, выявленные на основании показателей сравниваемых выборок.
2. Практика физической культуры и спорта показывает, что для спортивной работы достаточно принять надежность счета Р = 0, 95.
Для надежности счета: Р= 0, 95 (α = 0, 05), при числе степеней свободы k = n1 + п2 - 2 по таблице приложения находим величину критического (стандартного) значения критерия (tкр).
3. На основании свойств нормального закона распределения критерия Стьюдента осуществляется сравнение t и tкр.
Делаем выводы:
- если t ≥ tкр, то различие между сравниваемыми выборками статистически достоверно;
- если t < tкр, то различие статистически недостоверно.
Для исследователей в области физической культуры и спорта оценка статистической достоверности является первым шагом в решении конкретной задачи: принципиально или непринципиально различаются между собой сравниваемые выборки. Последующий шаг заключается в оценке этого различия с педагогической точки зрения, что определяется условием задачи.
Рассмотрим применение критерия Стьюдента на конкретно примере.
Пример. Группа испытуемых оценена на ЧСС (уд./мин) в количестве 18 человек до xi и в количестве 16 человек после yi разминки.
Оценить эффективность разминки по показателю ЧСС. Исходные данные и расчеты представлены в таблицах 9, 10.
Таблица 9
Обработка показателей ЧСС до разминки
| № п/п | xi | ni | xi ni | xi- 
| (xi-  )2 )2
| (xi-  )2 ni )2 ni
|
| -7 | ||||||
| -3 | ||||||
| -1 | ||||||
| Всего | - | - | - |


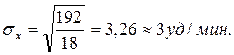
Таким образом, до разминки показатели группы составили:  ± σ х = (157 ± 3) уд./мин.
± σ х = (157 ± 3) уд./мин.
Таблица 10
Обработка показателей ЧСС после разминки
| № п/п | yi | ni | yi ni | yi- 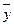
| (yi- 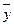 )2 )2
| (yi- 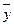 )2 ni )2 ni
|
| -5 | ||||||
| -3 | ||||||
| Всего | - | - | - |
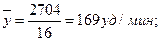

Таким образом, после разминки показатели группы составили 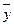 ± σ у = (169±3) уд./мин.
± σ у = (169±3) уд./мин.
Теперь определим обе ошибки репрезентативности. Выявляется различие между средними показателями и некоей огромной генеральной совокупностью N= ∞, которая нам фактически неизвестна и из которой и


