
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Плоскость
|
|
Точка
4.1.1. Сущность метода проекций.
4.1.2. Что такое проекция точки?
4.1.3. Как называются и обозначаются плоскости проекций?
4.1.4. Что такое линии проекционной связи на чертеже и как они располагаются на чертеже по отношению к осям проекций?
4.1.5. Как построить третью (профильную) проекцию точки?
4.1.6. Построить на трехкартинном чертеже три проекции точек А, В, С, записать их координаты и заполнить таблицу.
 |
А …, …, …
B …, …, …
С …, …, …
| Обозначение | Название элемента чертежа |
| П1 | |
| П2 | |
| П3 | |
| x, y, z | |
| A1 | |
| A2 | |
| A3 | |
| A1A2 | |
| A2A3 |
4.1.7. Построить недостающие оси проекций, хА=25, yA=20. Построить профильную проекцию точки А.

4.1.8. Построить три проекции точек по их координатам: А(25, 20, 15), В(20, 25, 0) и С(35, 0, 10). Указать положение точек по отношению к плоскостям и осям проекций. Какая из точек ближе к плоскости П3?

4.1.9. Материальные точки А и В начинают одновременно падать. В каком положении окажется точка В, когда точка А коснется земли? Определить видимость точек. Построить точки в новом положении.

4.1.10. Построить три проекции точки А, если точка лежит в плоскости П3, а расстояние от нее до плоскости П1 равно 20 мм, до плоскости П2 – 30 мм. Записать координаты точки.
Прямая
4.2.1. Чем может быть задана прямая линия на чертеже?
4.2.2. Какая прямая называется прямой общего положения?
4.2.3. Какое положение может занимать прямая относительно плоскостей проекций?
4.2.4. В каком случае проекция прямой обращается в точку?
4.2.5. Что характерно для комплексного чертежа прямой уровня?
4.2.6. Определить взаимное положение данных прямых.

a … b a … b a … b
4.2.7. Построить проекции отрезка прямой АВ длиной 20 мм, параллельного плоскостям: а) П2; б) П1; в) оси Ох. Обозначить углы наклона отрезка к плоскостям проекций.
a) б) в)
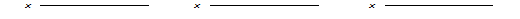
4.2.8. Построить проекции отрезка АВ по координатам его концов: А(30, 10, 10), В(10, 15, 30). Построить проекции точки С, делящей отрезок в отношении АС: СВ = 1: 2.

4.2.9. Определить и записать количество ребер данного многогранника и положение их относительно плоскостей проекций.

4.2.10. Через точку А провести горизонталь и фронталь, пересекающие прямую m.

4.2.11. Определить расстояние между прямой b и точкой А

4.2.12. Построить проекции отрезка АВ длиной 20 мм, проходящего через точку А и перпендикулярного плоскости а) П2; б) П1; в) П3.
а) б)

в)
Плоскость
4.3.1. Какими элементами пространства можно задать плоскость?
4.3.2. Как относительно плоскостей проекций может быть расположена плоскость?
4.3.3. Условие принадлежности точки плоскости, прямой плоскости.
4.3.4. Какими свойствами обладают плоскости проецирующие и уровня?
4.3.5. Какие линии уровня плоскости вы знаете? Как они изображаются на комплексном чертеже?
4.3.6. Определить расположение плоскостей Γ, Σ, Δ, Θ, Ω относительно плоскостей проекций. Заполнить таблицу.
| Чертежи | а) | б) | в) | г) | д) |
| Плоскость | Г(а ∩ b) | Σ (а || b) | Δ (а || b) | Θ (а ∩ b) | Ω (а ∩ b) |
| Расположение плоскости | |||||
| Название плоскости |
а) б) в) г) д)

4.3.7. Построить горизонтальную проекцию плоского пятиугольника АВСDЕ.
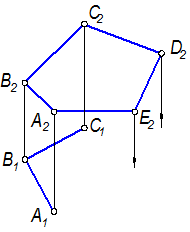
4.3.8. Построить недостающую проекцию точки А, принадлежащей плоскости Г(а∩ b), с помощью главных линий плоскости.

4.3.9. Построить фронтальную проекцию прямой m, лежащей в плоскости Σ (а || b).

5. Вопросы для самоконтроля и задачи для самостоятельной работы
по теме «Проекции с числовыми отметками»
5.1. Точка
5.1.1 Почему в решении задач горного и геологоразведочного производства широкое применение нашел метод проекций с числовыми отметками?
5.1.2. Какие новые относительные числовые отметки будут иметь точки А5, В12, С0, если новая плоскость проекций располагается выше плоскости П0 на 7 ед. масштаба.
5.1.3. Определите длину отрезка |А3В7, 25| на вертикальной прямой t.
5.1.4. По комплексному чертежу точек А, В, С, Д, Е построить их проекции на плане с указанием отметок.

5.1.5. Построить на плане произвольные точки: А, расположенную на 10 м выше По; В, расположенную на 7 м ниже плоскости По.

5.1.6. По заданному комплексному чертежу построить проекции точек А, В, С с числовыми отметками А(3, 0; 4, 5; 7, 5); В(4, 5; 0; 2, 6); С(7; 4; -2).
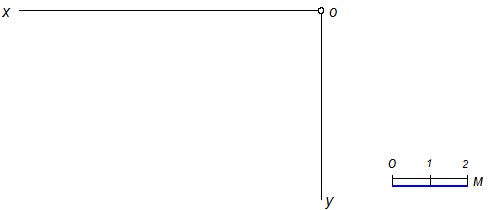
5.2. Прямая
5.2.1. Что такое азимут падения и угол падения наклонной прямой?
5.2.2. Чему равно заложение прямой, если ее угол падения равен 45°?
5.2.3. Как отличить на плане пересекающиеся и скрещивающиеся прямые?
5.2.4. Каковы условия параллельности двух прямых, заданных на плане?
5.2.5. В каком случае прямой угол проецируется на план без искажения в виде прямого угла?
5.2.6. Построить точку С, лежащую на прямой, с числовой отметкой 9.

5.2.7. На прямой АВ определить отметку точки С, если АС=2СВ. Через точку D провести прямую DЕ, параллельную АВ.

5.2.8.Укажите точку М, в которой острие шеста, падающего по направлению S, воткнулось в землю. Определить уклон прямой АВ.

5.2.9. На заданной прямой определить отметку точки В.

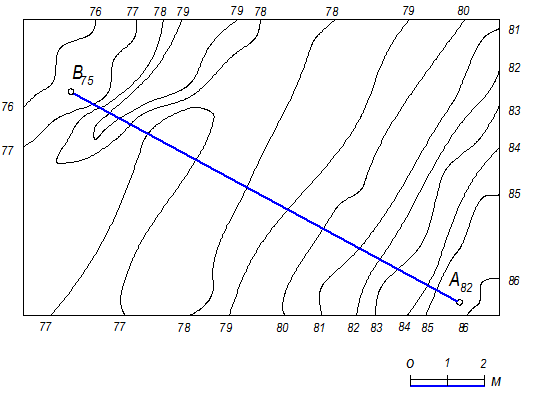
5.2.10. Определить длину прямой между точками А и В и угол ее наклона к горизонту.
а)

б)

5.2.11. Построить профиль прямой n(С8; α = 30°). Определить отметку точки D.

5.2.12. Определить, пересекаются ли заданные прямые АВ и СD двумя способами.

5.2.13. Определить, перпендикулярны ли прямая АВ и прямая m.

5.2.14. Через точку В провести: а) прямую, которая скрещивалась бы с прямой n (С8Ð 40°) под углом 90°; б) прямую, параллельную прямой n.
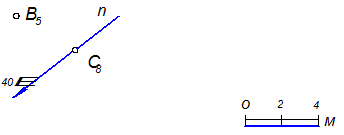
5.2.15. Прямые m и n пересекаются в точке С. Определить истинную величину отрезков АС и ВС и их углы наклона.
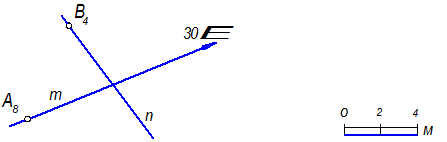
5.2.16. Через точку F(F7) провести горизонтальную прямую h, которая пересекала бы прямую n(А10, В5).

5.3. Плоскость
5.3.1. Какие существуют способы задания наклонной плоскости на плане?
5.3.2. Как будет проецироваться на плане фигура, лежащая в вертикальной плоскости?
5.3.3. Почему в запись элементов залегания наклонной плоскости входит азимут падения, а не азимут простирания?
5.3.4. Укажите алгоритм решения задачи на пересечение прямой и плоскости.
5.3.5. Как провести плоскость через прямую m параллельно заданной прямой n?
5.3.6. Построить линию пересечения двух плоскостей Рi и Σ i.

5.3.7. Определить линию пересечения плоских откосов Рi и Qi.

5.3.8. Определить направление простирания и угол наклона пласта горной породы (известняка). (На чертеже нанесены три скважины). Данные бурения показали, что в скважине №1 пласт известняка встретился на глубине 1, 3 м от поверхности земли. В скважине №2 - на глубине 7, 6 м., а в скважине №3 - на глубине 5, 8 м.

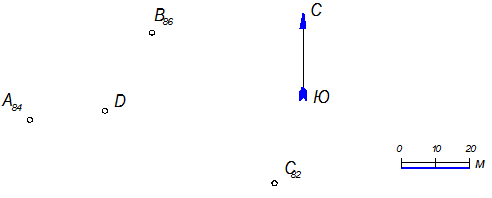
5.3.9. При бурении скважин вскрыто зеркало грунтовых вод. Определите по трем скважинам А, В, С уклон и направление движения грунтовых вод, а также отметку точки D, принадлежащей плоскости А, В, С.
5.3.10. Построить плоскость Р, Р' с уклоном 3/2 и проходящую через прямую А6В2.

5.3.11. Построить точку Е пересечения прямой MN с плоскостью АВС.

5.3.12. Через точку А провести плоскость Ψ, угол падения которой 32°, а азимут простирания 147°. Определить азимут линии падения этой плоскости.
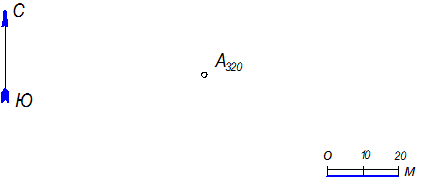
5.4. Поверхности
5.4.1. Перечислите известные виды правильных многогранников, укажите их характерные признаки.
5.4.2. Как задаются пирамида, конус и сфера на плане?
5.4.3. К какому типу поверхностей относится топографическая поверхность? Как ее можно задать на плане?
5.4.4. Построить линию пересечения конической поверхности Ψ (S14h9) с плоскостью Pi.

5.4.5. Построить линию пересечения плоскости Рi и рельефа местности.

5.4.6. Построить линию пересечения плоскости Рi с топографической поверхностью.

5.4.7. Построить горизонтали топографической поверхности определяемой точками А, В, С, D, Е, F, L c высотой сечения 1м.

5.4.8. Найти точки, в которых газопровод АВ выходит на поверхность земли.
5.4.9. Построить границы откосов насыпи наклонного участка дороги на круговой кривой. Имеющий уклон i=1: 1, 5.

5.4.10. Определить границы насыпей и выемок горизонтальной строительной площадки и аппарели. Имеющих уклон аппарели iапп=1: 3. Уклоны откосов насыпи iн=2: 3, уклоны выемок iв=1: 2.

|