Тангенциальная составляющая ускорения 10 страница

где dU — бесконечно малое изменение внутренней энергии системы, dA — элементар­ная работа, dQ — бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а dA и dQ таковыми не являются. В дальнейшем будем использовать запись первого начала термодинамики в форме (51.2).

Из формулы (51.1) следует, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж).

Если система периодически возвращается в первоначальное состояние, то измене­ние ее внутренней энергии D U =0. Тогда, согласно первому началу термодинамики,

т. е. вечный двигатель первого рода — периодически действующий двигатель, который совершал бы бó льшую работу, чем сообщенная ему извне энергия, — невозможен (одна из формулировок первого начала термодинамики).

§ 52. Работа газа при изменении его объема

Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, находя­щийся под поршнем в цилиндрическом сосуде (рис. 78). Если газ, расширяясь, пере­двигает поршень на бесконечно малое расстояние d l, то производит над ним работу

где S — площадь поршня, S d l=dV— изменение объема системы. Таким образом,

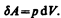(52.1)

Полную работу А, совершаемую газом при изменении его объема от V ₁ до V ₂, найдем интегрированием формулы (52.1):

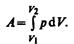(52.2)

Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (52.2) справедливо при любых изменениях объема твердых, жидких и газообразных тел.

Произведенную при том или ином процессе работу можно изобразить графически с помощью кривой в координатах р, V. Пусть изменение давления газа при его расширении изображается кривой на рис. 79. При увеличении объема на dV соверша­емая газом работа равна pdV, т. е. определяется площадью полоски с основанием dV, заштрихованной на рисунке. Поэтому полная работа, совершаемая газом при расшире­нии от объема V ₁ до объема V ₂, определяется площадью, ограниченной осью абсцисс, кривой p = f(V) и прямыми V ₁ и V ₂.

Графически можно изображать только равновесные процессы — процессы, состо­ящие из последовательности равновесных состояний. Они протекают так, что измене­ние термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесны (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медлен­нее процесс протекает, тем он ближе к равновесному). В дальнейшем рассматриваемые процессы будем считать равновесными.

§ 53. Теплоемкость

Удельная теплоемкость вещества — величина, равная количеству теплоты, необходи­мому для нагревания 1 кг вещества на 1 К:

Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кг × К)).

Молярная теплоемкость —величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:

(53.1)

где n= m / М — количество вещества.

Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(моль × К)).

Удельная теплоемкость с связана с молярной С _m, соотношением

(53.2)

где М — молярная масса вещества.

Различают теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным.

Запишем выражение первого начала термодинамики (51.2) для 1 моль газа с учетом формул (52.1) и (53.1):

(53.3)

Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю (см. (52.1)) и сообщаемая газу извне теплота вдет только на увеличение его внутренней энергии:

(53.4)

т. е. молярная теплоемкость газа при постоянном объеме С_V равна изменению внут­ренней энергии 1 моль газа при повышении его температуры на 1 К. Согласно формуле (50.1), тогда

(53.5)

Если газ нагревается при постоянном давлении, то выражение (53.3) можно запи­сать в виде

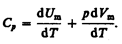
Учитывая, что не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна С_V (см. (53.4)), и дифференцируя уравнение Клапейрона — Менделеева pV_m=RT (42.4) по T (p =const), получаем

(53.6)

Выражение (53.6) называется уравнением Майера; оно показывает, что С_р всегда больше С_V на величину молярной газовой постоянной. Это объясняется тем, что при нагрева­нии газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, таккак постоянство давления обеспечивается увеличением объема газа. Использовав (53.5), выражение (53.6) можно записать в виде

(53.7)

При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение С_p к С_V :

(53.8)

Из формул (53.5) и (53.7) следует, что молярные теплоемкости определяются лишь числом степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов.Уже у двухатомных газов число степеней свободы, проявля­ющееся в теплоемкости, зависит от температуры. Молекула двухатомного газа облада­ет тремя поступательными, двумя вращательными и одной колебательной степенями свободы.

По закону равномерного распределения энергии по степеням свободы (см. § 50), для комнатных температур С_V = ⁷ / ₂ R. Из качественной экспериментальной зависимости молярной теплоемкости С_V водорода (рис. 80) следует, что С_V зависит от темпера­туры: при низкой температуре (»50 К) С_V = ³ / ₂ R, при комнатной — C_V = ⁵ / ₂ R (вместо расчетных ⁷/₂ R) и при очень высокой — Сv= ⁷/₂ R. Это можно объяснить, пред­положив, что при низких температурах наблюдается только поступательное движение молекул, при комнатных — добавляется их вращение, а при высоких — к этим двум видам движения добавляются еще колебания молекул.

Расхождение теории и эксперимента нетрудно объяснить. Дело в том, что при вычислении теплоемкости надо учитывать квантование энергии вращения и колебаний молекул (возможны не любые вращательные и колебательные энергии, а лишь опреде­ленный дискретный ряд значений энергий). Если энергия теплового движения недоста­точна, например, для возбуждения колебаний, то эти колебания не вносят своего вклада в теплоемкость (соответствующая степень свободы «замораживается» — к ней неприменим закон равнораспределения энергии). Этим объясняется, что теплоемкость моля двухатомного газа — водорода — при комнатной температуре равна ⁵/₂ R вме­сто ⁷/₂ R. Аналогично можно объяснить уменьшение теплоемкости при низкой тем­пературе («замораживаются» вращательные степени свободы) и увеличение при высо­кой («возбуждаются» колебательные степени свободы).

§ 54. Применение первого начала термодинамики к изопроцессам

Среди равновесных процессов, происходящих с термодинамическими системами, выде­ляются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.

Изохорный процесс (V =const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 81), где процесс 1—2 есть изохорное нагревание, а 1 — 3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.

Как уже указывалось в § 53, из первого начала термодинамики (dQ= d U+dA)дляизохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:

Согласно формуле (53.4),

Тогда для произвольной массы газа получим

(54.1)

Изобарный процесс (p =const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа (см. (52.2)) при увеличения объема от V ₁ до V ₂ равна

(54.2)

и определяется площадью заштрихованного прямоугольника (рис. 82). Если испо­льзовать уравнение (42.5) Клапейрона — Менделеева для выбранных нами двух состояний, то

откуда

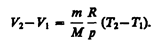
Тогда выражение (54.2) для работы изобарного расширения примет вид

(54.3)

Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T ₂ — T ₁ =1 К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.

В изобарном процессе при сообщении газу массой т количества теплоты

его внутренняя энергия возрастает на величину (согласно формуле (53.4))

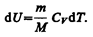
При этом газ совершит работу, определяемую выражением (54.3).

Изотермический процесс (T =const). Как уже указывалось § 41, изотермический процесс описывается законом Бойля—Мариотта:

Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу (см. рис. 60), расположенную на диаграмме тем выше, чем выше тем­пература, при которой происходит процесс.

Исходя из выражений (52.2) и (42.5) найдем работу изотермического расширения газа:

Так как при Т =const внутренняя энергия идеального газа не изменяется:

то из первого начала термодинамики (dQ= d U+dA) следует, что для изотермического процесса

т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:

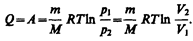(54.4)

Следовательно, для того чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

§ 55. Адиабатический процесс. Политропный процесс

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ= 0)между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно счи­тать процесс распространения звука в среде, так как скорость распространения звуко­вой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д.

Из первого начала термодинамики (dQ= d U+dA) для адиабатического процесса следует, что

(55.1)

т. е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя выражения (52.1) и (53.4), для произвольной массы газа перепишем уравнение (55.1) в виде

(55.2)

Продифференцировав уравнение состояния для идеального газа получим

(55.3)

Исключим из (55.2) и (55.3) температуру Т.

Разделив переменные и учитывая, что С_p/С_V=g (см. (53.8)), найдем

Интегрируя это уравнение в пределах от p ₁ до p ₂ и соответственно от V ₁ до V ₂, а затем потенцируя, придем к выражению

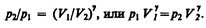
Так как состояния 1 и 2 выбраны произвольно, то можно записать

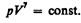(55.4)

Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или p, Т исключим из (55.4) с помощью уравнения Клапейрона — Менделеева

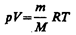
соответственно давление или объем:

(55.5)

(55.6)

Выражения (55.4) — (55.6) представляют собой уравнения адиабатического процес­са. В этих уравнениях безразмерная величина (см. (53.8) и (53.2))

(55.7)

называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i =3, g=1, 67. Для двухатомных газов (Н2, N2, О2 и др.) i= 5, g =1, 4. Значения g, вычисленные по формуле (55.7), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой (рис. 83). На рисунке видно, что адиабата (pV^g = const) более крута, чем изотерма (pV = const). Это объясняется тем, что при адиабатическом сжатии 1 — 3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем урав­нение (55.1) в виде

Если газ адиабатически расширяется от объема V ₁ до V ₂, то его температура уменьша­ется от T ₁ до T ₂ и работа расширения идеального газа

(55.8)

Применяя те же приемы, что и при выводе формулы (55.5), выражение (55.8) для работы при адиабатическом расширении можно преобразовать к виду

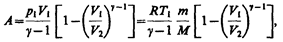
где .

Работа, совершаемая газом при адиабатическом расширении 1—2 (определяется площадью, заштрихованной на рис. 83), меньше, чем при изотермическом. Это объяс­няется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны С_V и С _p, в изотермическом процессе (d T=0) теплоемкость равна ±¥, в адиабатическом (dQ =0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости (C =const) можно вывести уравнение политропы:

(55.9)

где п=(С—С_p)/(С—С_V)— показатель политропы. Очевидно, что при С =0, n = g, из (55.9) получается уравнение адиабаты; при С = ¥, n = 1 — уравнение изотермы; при С = С_p, n =0 —уравнение изобары, при С=С_V, n =±¥ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.

§ 56. Круговой процесс (цикл). Обратимые и необратимые процессы

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изоб­ражается замкнутой кривой (рис. 84). Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1 — 2) и сжатия (2 — 1) газа. Работа расширения (определяется площадью фигуры 1a2V ₂ V ₁ 1) положительна (d V > 0), работа сжатия (определяется площадью фигуры 2b1V ₁ V ₂ 2) отрицательна (d V< 0 ). Следовательно, работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой. Если за цикл совершается положительная работа A= > 0 (цикл протекает по часовой стрелке), то он называется прямым (рис. 84, а), если за цикл совершается отрицательная работа A= < 0 (цикл протекает против часовой стрелки), то он называется обратным (рис. 84, б).

Прямой цикл используется в тепловых двигателях — периодически действующих двигателях, совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах — периодически действующих установках, в ко­торых за счет работы внешних сил теплота переносится к телу с более высокой температурой.

В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю. Поэтому первое начало термодинамики (51.1) для кругового процесса

(56.1)

т. е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому

где Q ₁ — количество теплоты, полученное системой, Q ₂ — количество теплоты, отданное системой. Поэтому термический коэффициент полезного действия для кругового процесса

(56.2)

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среда и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Любой равновесный процесс является обратимым. Обратимость равновесного процесса, происходящего в системе, следует из того, что се любое промежуточное состояние есть состояние термодинамического равновесия; для него «безразлично», идет процесс в прямом или обратном направлении. Реальные процессы сопровождают­ся диссипацией энергии (из-за трения, теплопроводности и т. д.), которая нами не обсуждается. Обратимые процессы — это идеализация реальных процессов. Их рассмот­рение важно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют мак­симальный термический коэффициент полезного действия, что позволяет указать пути повышения к. п. д. реальных тепловых двигателей.

§ 57. Энтропия, ее статистическое толкование и связь с термодинамической вероятностью

Понятие энтропии введено в 1865 г. Р. Клаузиусом. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты.

Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно dQ/T. Строгий теоретический анализ показывает, что приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю:

(57.1)

Из равенства нулю интеграла (57.1), взятого по замкнутому контуру, следует, что подынтегральное выражение dQ/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Таким образом,

(57.2)

Функция состояния, дифференциалом которой является dQ/T, называется энтропией и обозначается S.

Из формулы (57.1) следует, что для обратимых процессов изменение энтропии

(57.3)

В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:

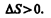(57.4)

Выражения (57.3) и (57.4) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (57.3) и (57.4) можно представить в виде неравенства Клаузиуса

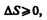(57.5)

т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (57.2), изменение энтропии

(57.6)

где подынтегральное выражение и пределы интегрирования определяются через вели­чины, характеризующие исследуемый процесс. Формула (57.6) определяет энтропию лишь с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий.

Исходя из выражения (57.6), найдем изменение энтропии в процессах идеального газа. Taк как то

или

(57.7)

т. е. изменение энтропии D S _1®2 идеального газа при переходе его из состояния 1 в со­стояние 2 не зависит от вида процесса перехода 1 ® 2.

Таккак для адиабатического процесса dQ = 0, то D S = 0 и, следовательно, S= const, т. е. адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом. Из формулы (57.7) следует, что при изотермическом процессе (T ₁= T ₂)

при изохорном процессе (V ₁ = V ₂)

Энтропия обладает свойством аддитивности: энтропия системы равна сумме энт­ропий тел, входящих в систему. Свойством аддитивности обладают также внутренняя энергия, масса, объем (температура и давление таким свойством не обладают).

Более глубокий смысл энтропии вскрывается в статистической физике: энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению, W³ 1, т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя £ 1!)).

Согласно Больцману (1872), энтропия системы и термодинамическая вероятность связаны между собой следующим образом:

(57.8)

где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана (57.8) позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядо­ченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом мак­симальна и энтропия.