
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Шифр Фейстеля (Файстеля - Feistel)
|
|
Для шифру Фейстеля характерно:
1. Вхідний блок для кожного перетворення розбивається на дві половини: p=(l, r), де l -ліва, r -права
2. Використовується перетворення вигляду Fi (l, r)=(r, l  fi (r)), де fi – функція, що залежить від ключа Ki, а
fi (r)), де fi – функція, що залежить від ключа Ki, а  - операція XOR чи деяка інша.
- операція XOR чи деяка інша.
Функція fi називається цикловою функцією, а ключ Ki, що використовується для отримання функції fi називається цикловим ключем. Можна помітити, що з циклової функції складається лише ліва частина, а права залишається незмінною. Після цього обидві половини міняються місцями. Таке перетворення прокручується декілька разів (декілька циклів) і виходом шифру є отримана в кінці пара (l, r) Графічо все виглядає приблизно так (див. мал. 2-1):
В якості функції fi може виступати деяка комбінація перестановок, підстановок, зсувів, додавань ключа та інших перетворень. Так при використанні підстановок інформація проходить через спеціальні блоки, що називаються S-блоками (S-боксами, S-boxes), в яких значення групи бітів заміняється на інше значення. По такому принципу (за винятком деяких відмінностей) побудовано багато алгоритмів: DES, FEAL, серия LOKI
Алгоритми, побудовані по SP-принципу (SP-мережі)
- здійснюють перетворення, пропускаючи блок через послідовність підстановок (Substitutions) і перестановок (Permutations). Звідси і назви – SP [4] -мережі тобто мережі підстановок, перестановок.
- 
| Мал. 2‑ 1 |
Отримання циклових ключів.
Ключ має фіксовану довжину. Однак при прокрутці хоча б 8-ми циклів шифрування з розміром блока 128 біт навіть при простому додаванні за допомогою XOR потрібно буде 8*128=1024 біта ключа, так як не можна додавати в кожному циклі одне і теж значення – так як це призводить до послаблення шифру. Тому для одержання послідовності ключових біт придумується спеціальний алгоритм вироблення циклових ключів (розклад ключів- key schedule). В результаті роботи цього алгоритму із вихідних біт ключа шифрування отримується масив біт визначеної довжини, з якого за певними правилами складаються циклові ключі. Кожен шифр має свій алгоритм вироблення циклових ключів.
Режим роботи блочних шифрів.
Для того щоб використовувати алгоритми блочного шифрування для різних криптографічних задач, існує декілька режимів їх роботи. Найчастіше на практиці використовуються наступні режими:
- Електронна кодова книга - ECB (Electronic Code Book);
- Зчеплення блоків шифротексту - CBC (Cipher Block Chaining);
- Зворотній зв’язок по шифротексту - CFB (Cipher Feed Back);
- Зворотній зв’язок по виходу - OFB (Output Feed Back);
Зробимо наступне позначення: застосування шифру до блоку відкритого тексту позначимо так: Ek(M)=C, де k - ключ, M – блок відкритого тексту, а C – отриманий шифрований текст.
Електронна кодова книга (ECB)
Вихідний текст розбивається на блоки, рівні за розміром розміру блоку шифру. Після цього кожен блок шифрують незалежно від інших з використанням одного ключа шифрування. Графічно це виглядає так (див. мал. 2-2):
| Мал. 2‑ 2 |
 Безпосередньо даний режим застосовується для шифрування невеликих об’ємів інформації, розміром не більше одного блока чи для шифрування ключів. Це пов’язано з тим, що однакові блоки відкритого тексту перетворюються в однакові блоки шифрованого тексту, а це може дати додаткову інформацію зловмиснику для здійснення криптоаналізу. Крім того відкритий текст може містити так звані слова підказки (на приклад „Доброго дня” чи „до побачення”), тоді зловмисник буде мати відповідники шифрованого та відкритого текстів для криптоаналізу. Відповідно шанси знаходження правильного ключа значно зростають.
Безпосередньо даний режим застосовується для шифрування невеликих об’ємів інформації, розміром не більше одного блока чи для шифрування ключів. Це пов’язано з тим, що однакові блоки відкритого тексту перетворюються в однакові блоки шифрованого тексту, а це може дати додаткову інформацію зловмиснику для здійснення криптоаналізу. Крім того відкритий текст може містити так звані слова підказки (на приклад „Доброго дня” чи „до побачення”), тоді зловмисник буде мати відповідники шифрованого та відкритого текстів для криптоаналізу. Відповідно шанси знаходження правильного ключа значно зростають.
- Основна перевага такого методу – простота реалізації
Зчеплення блоків шифротексту (CBC [5])
- даний режим шифрування приміняється найбільчасто для обробки великих об’ємів інформації
- вихідний текст розбивається на блоки, а потім обробляється за наступною схемою:
- Перший блок складається побітно по модулю 2 (XOR) з деяким значенням IV - початковим вектором (Init Vector), котрий вибирається незалежно перед початком шифрування.
- Отримане значення шифрується
- Отриманий в результаті блок шифротексту відправляється одержувачу і одночасно служить по-чатковим век-тором IV для наступного блоку від-критого тек-сту
- Розшифровка проводиться у зворотному порядку
Графічний вигляд даної схеми (див. мал. 2-3):
- У вигляді формули, перетворення в режимі CBC[6] можна представити так: Ci=Ek(Mi  Ci-1), де i – номер відповідного блока.
Ci-1), де i – номер відповідного блока.
- Використання такого зчеплення блоків шифрованого тексту з відкритим текстом дозволяє позбутися недоліків методу ECB так як кожен наступний блок залежить від усіх попередніх. Якщо під час передачі один із блоків зазнає пошкодження (передасться із помилками), то одержувач зможе розшифрувати лише попередні блоки повідомлення.
- Важлива властивість такого методу – поширення помилки. Зміна блока відкритого тексту міняє усі наступні блоки шифротексту.
-
| Мал. 2‑ 3 |
 Таким чином останній блок шифротексту залежить від усіх попередніх і може використовуватися для перевірки цілісності та аутентичності повідомлення. Такий блок називається кодом аутентифікації повідомлення (MAC - Message Authentication Code). Такий код дозволяє захистити повідомлення як від випадкових так і навмисних змін у повідомленні.
Таким чином останній блок шифротексту залежить від усіх попередніх і може використовуватися для перевірки цілісності та аутентичності повідомлення. Такий блок називається кодом аутентифікації повідомлення (MAC - Message Authentication Code). Такий код дозволяє захистити повідомлення як від випадкових так і навмисних змін у повідомленні.
Зворотній зв’язок по шифротексту (CFB [7])
Даний режим може використовуватися для отримання з поточного шифру в блочний. Розмір блока в даному режимі менший або рівний розміру блока шифру. Схема даного режиму (див. мал. 2-4):

Мал. 2‑ 4
1. IV представляє собою реєстр зсуву. Спочатку IV заповнюється деяким значенням, яке називається синхропосилкою, не є таємним і передається перед сеансом зв’язку одержувачу.
2. Значення IV шифрується
3. беруться перші k біт зашифрованого значення IV і складаються (XOR) з k бітами відкритого тексту. В результаті отримується блок шифротексту з k біт.
4. Значення IV зсувається на k біт вліво, а замість нього ставиться значення шифрованого тексту.
5. Після цього знову повторюється пункт 2 і так до кінця.
- Розшифровування проводиться аналогічно
- Особливість даного методу – помилка поширюється на весь текст
- Рекомендовані значення для k: 1< =k< =8.
- Використовується для шифрування потоків інформації (оцифроване відео, аудіо)
Зворотній зв’язок по виходу (OFB)
Даний режим характерний тим, що дозволяє отримати поточний шифр в його класичному вигляді на відміну від режиму CFB[8], в якому присутній зв’язок з шифротекстом. Принцип роботи схожий з принципом роботи режиму CFB, але реєстр зсуву IV заповнюється не бітами шифротексту, а бітами, що залишаються після усікання. Його схема така (див. мал. 2-5)
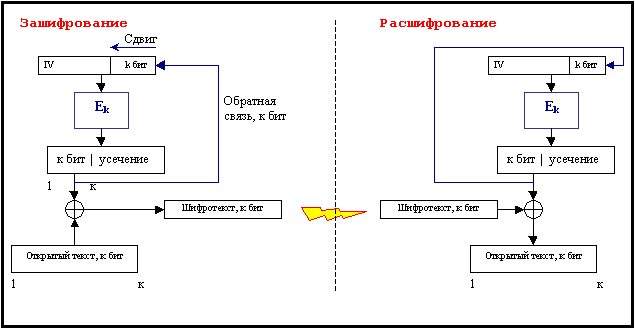
Мал. 2‑ 5
Для б-якого блока довжиною k операція за шифрування має наступний вигляд: Ci=Mi  Gi, де Gi – результат за шифрування деякого вектора, який є заповненням вектора зсуву.
Gi, де Gi – результат за шифрування деякого вектора, який є заповненням вектора зсуву.
- головна особливість – не поширюються одиничні помилки, так як заповнення зсувів реєстру відбувається незалежно від шифрованого тексту.
- Застосовується для за шифровки потоків аудіо, відео чи потоків інформації, що вимагають оперативної доставки.
- Широко використовуються у військовій галузі на рівні із поточними шифрами
Аутентифікація повідомлень з допомогою блочних шифрів.
Аутентифікація (authentification) – превірка справжності чого не-будь чи кого не-будь. Може бути аутентифікація користувача, повідомлення і т.п. Аутентифікацію потрібно відрізняти від наступного поняття:
Ідентифікація (Identification) – деяке описове представлення якого не-будь суб’єкта. Так наприклад якщо хтось заявляє що він Вася Іванов, то він себе ідентифікує як “Вася Іванов”. Але перевірити так це чи ні насправді (провести аутентифікацію) можна з допомогою його паспорта.
Отже тепер щодо перевірки автентичності з допомогою блочних шифрів.
- Відправник А бажає відправити деяке повідомлення (a1,.., at). Він здійснює зашифровування повідомлення з використанням таємного ключа, який відомий лише йому та одержувачу, в режимі CBC [9] чи CFB [10]. Після цього з отриманого шифротексту бере останній блок bt з к біт (при цьому к повинно бути достатньо велике).
- Відправник А відсилає повідомлення (a1,.., at, bt) одержувачу у відкритому вигляді або зашифрувавши на іншому ключі.
- Одержувач В, отримавши повідомлення (a1,.., at, bt), здійснює зашифровування (a1,.., at), в тому ж режимі що і А (повинна існувати домовленість) на тому ж таємному ключі (який відомий лише йому та А).
- Порівнюючи отриманий результат з bt він переконується, що повідомлення відправив А, що воно не було підроблено під час пересилки у відкритому вигляді.
В даній схемі bt є кодом аутентифікації повідомлення (MAC[11]).
Зауваження:
Режим шифрування повинен обов’язково бути із поширенням помилок тобто CBC[12] CFB[13].
Необхідно використовувати шифр з достатньою довжиною блоку, так як може бути ситуація: для малих блоків при заміні вихідного повідомлення існує велика імовірність отримати такий самий код аутентифікації
Крім того абоненти повинні мати один і той же таємний кюч.
Л №8
Поточні шифри
Будова шифрів
Шифрування здійснюється на основі складання деякої ключової послідовності (гами) із відкритим текстом повідомлення. Складання здійснюється по знаково через використання функції XOR. Рівняння зашифровування має наступний вигляд:
ci = mi Å ki для i =1, 2, 3... (навести приклад)
тут ci - знак шифротексту, mi - знак відкритого тексту, ki - знак ключової послідовності. Розшифрування має такий вигляд:
mi = ci Å ki для i =1, 2, 3...

| Мал. 3‑ 1 |
- синхронні
- асинхронні (самосинхронізуючі)
Синхронні поточні шифри
ключовий потік (вихідна гама) отримується незалежно від вихідного та шифрованого текстів. В цьому випадку схема має такий вигляд (див. мал. 3-2):
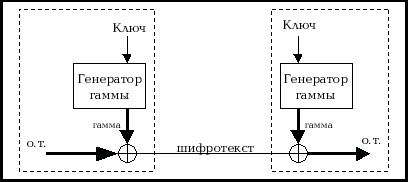
| Мал. 3‑ 2 |
На послідовність, що виробляється накладаються певні вимоги. Так при великій кількості нулів у послідовності зашифрований фрагмент буде відісланий просто у вихідному вигляді. Аналогічна ситуація буде спостерігатися, якщо послідовність містить велику кількість одиниць. В даному випадку для зловмисника буде досить легко спробувати у якості гами послідовність одиниць, відповідно після накладання буде отриманий фрагмент відкритого тексту (зазвичай при програмному підборі гами такі гами застосовуються перші, як найпростіші). Тому найкраща гама – це випадкова послідовність. Але тут постає наступна проблема – не можна незалежно згенерувати дві однакові випадкові послідовності.
Генератори гами виробляють так звані псевдовипадкові послідовності, які залежать від ключа шифрування, але схожі своїми характеристиками з випадковими. Причому ставиться наступна умова: при наявності деякої визначеної кількості біт гами повинно бути неможливо передбачити наступні біти гами (послідовності). Крім цього на вході повинна бути однаково імовірна поява одинички чи нулика. Для досягнення цих умов отримані послідовності (гами) досліджуються статистичними тестами.
На сьогоднішній день генерування псевдовипадкових послідовностей є першочерговим завданням криптографії. Тому існує досить багато генераторів, та статистичних тестів для перевірки вихідних послідовностей.
Властивості синхронних поточних шифрів
- Вимоги по синхронізації. При використовуванні синхронних поточних шифрів одержувач та відправник повідомлення повинні бути синхронізовані – тобто повинні вибрати однакове значення ключового потоку для відповідних знаків потоку даних, що передаються. При порушенні синхронізації (наприклад втрата знака при передачі), процес розшифровування не дасть потрібного результату.
- Відсутність розмноження помилок. Зміна знаку шифротексту при передачі не викликає помилок при розшифровуванні інших знаків шифротексту.
- Властивість активної атаки. Як наслідок першої властивості будь-яка вставка чи видалення символу в шифротексті активним зловмисником приводить до порушення синхронізації і дозволяє одержувачу виявити несанкціоноване втручання. Як наслідок другої властивості, активний зловмисник може змінити символи шифротексту і такі зміни приведуть до відповідних змін у відкритому тексті, що отримується під час розшифровування. Тому необхідні додаткові механізми захисту, що дозволять запобігти цьому.
Приклад атаки зловмисника на такі шифри:
O 1 O 2 O 3... – знаки відкритого тексту.

| Мал. 3‑ 3 |
С 1 С 2 С 3... – знаки шифротексту, отримані наступним чином (див. мал. 2-3):
Припустимо, що при повторному шифруванні відбулася вставка одного знака O' (див. мал. 3-3, 3-4):
Криптоаналітик зловмисника перехватив обидві послідовності C 1 C 2 C 3 C 4 і C 1 C '2 C '3 C '4. Склавши наступні рівняння: К 2= C '2  O '; O 2= C 2
O '; O 2= C 2  К 2; К 3= C '3
К 2; К 3= C '3  O 2; O 3= C 3
O 2; O 3= C 3  К 3 і так далі і підібравши значення одного знаку O ' він зможе прочитати повідомлення після цього знаку. В результаті дослідження криптоаналітик зловмисника отримає фрагмент ключової послідовності (гами). При потребі він може спробувати побудувати усю гаму і таким чином розшифрує усе повідомлення. Тому можна зробити висновок: один і той же ключ не можна використовувати двічі.
К 3 і так далі і підібравши значення одного знаку O ' він зможе прочитати повідомлення після цього знаку. В результаті дослідження криптоаналітик зловмисника отримає фрагмент ключової послідовності (гами). При потребі він може спробувати побудувати усю гаму і таким чином розшифрує усе повідомлення. Тому можна зробити висновок: один і той же ключ не можна використовувати двічі.

| Мал. 3‑ 4 |
Для ситуації коли однакові ключі використовуються для за шифровки різних текстів зловмисник може скористатися наступним способом: Обчислюється сума знаків шифротексту Ci 1  Ci 2 = Oi 1
Ci 2 = Oi 1  Кi
Кi  Кi
Кi  Oi 2= Oi 1
Oi 2= Oi 1  Oi 2, де Ci 1- i- й знак першого шифротексту, Ci 2 - i- й знак другого шифротексту, Oi 1 та Oi 2 – знаки відкритих текстів відповідно. (Навести приклад) Сума відкритих текстів не є випадковою, тому зловмисник зможе відтворити два повідомлення.
Oi 2, де Ci 1- i- й знак першого шифротексту, Ci 2 - i- й знак другого шифротексту, Oi 1 та Oi 2 – знаки відкритих текстів відповідно. (Навести приклад) Сума відкритих текстів не є випадковою, тому зловмисник зможе відтворити два повідомлення.
Самосинхронізуючі поточні шифри
- кожен знак ключового потоку визначається фіксованим числом попередніх знаків шифротексту. Схематично це може бути зображено так (див. мал. 3-5):

Мал. 3‑ 5
Даному типу шифрів відповідають блочні шифри, що працюють в режимі CFB[15]
Властивості самосинхронізуючих шифрів
- Самосинхронізація. Самосинхронізація існує при видаленні чи вставці деяких знаків шифротексту, так як процес зашифровування залежить від деякого фіксованого числа попередніх знаків шифротексту. Це значить, що у випадку видалення знаку із шифротексту спочатку будуть помилки у розшифровці, а потім вони зникнуть.
- Обмежене розмноження помилок. Припустимо, що стан шифру залежить від t попередніх знаків шифротексту. Якщо під час передачі один зі знаків шифротексту був змінений, чи видалений, чи вставлений, то при розшифровуванні буде спотворено не більше t знаків, після яких розшифрування знову буде нормальним.
- Властивість активної атаки. Виходячи з другої властивості можна зробити висновок, що будь-яка зміна знаків шифротексту зловмисником приведе до того, що декілька знаків буде розшифровано неправильно. Імовірність помітити це одержувачу є більшою в порівнянні з синхронними шифрами. Однак з іншої сторони, якщо зловмисник проведе не заміну, а вставку чи видалення знаку шифротексту, то (виходячи з першої властивості) це буде помітити набагато складніше ніж для синхронних шифрів. Тому також потрібні додаткові методи чи механізми для контролю такої ситуації.
- Розсіювання статистики відкритого тексту. Так як кожен знак відкритого тексту впливає на весь наступний шифротекст, статистичні властивості відкритого тексту не зберігаються в шифротексті.
Л №9, 10
Асиметричні криптосистеми
Асиметричні шифри використовують різні системи для зашифровування та розшифровування. В більшості таких систем перетворення визначається ключем, тобто два різних ключа – таємний та відкритий. Відкритий ключ опубліковується та може бути використаний для зв’язку із власником даного ключа. В основі асиметричних криптосистем лежить поняття односторонньої функції.
Односторонні функції
Одностороння (однонаправлена) функція (one way function) – це функція f, що здійснює відображення X  Y, де X и Y – довільні множини, що відповідають наступним умовам:
Y, де X и Y – довільні множини, що відповідають наступним умовам:
-
 x
x  X (області визначення) легко обчислити y=f(x), y
X (області визначення) легко обчислити y=f(x), y  Y.
Y. - Майже для будь-якого y
 Y (області значень) знайти f -1(y), тобто x, для якого y = f (x), обчислити неможливо.
Y (області значень) знайти f -1(y), тобто x, для якого y = f (x), обчислити неможливо.
Чому у визначенні стоїть майже для „будь-якого”? Тому що якщо взяти будь-яке x та обчислити для нього y = f (x), то ми вже будемо знати, що отриманому у відповідає взяте нами х. Збережемо ці два значення, і якщо ми коли-небудь зустрінемося з таким у, то ми відповідно знайдемо х.
Прикладом односторонньої функції може бути обчислення ax mod n, де a та n деякі числа. Така задача називається задачею одностороннього логарифмування. На даний момент не існує ефективних алгоритмів, що дозволяють вирішити цю задачу для великих чисел за прийнятний час. Взагалі даний приклад можна назвати односторонньою функцією з деякою натяжкою, тому що якщо з’явиться такий алгоритм, або надзвичайно зростуть обчислювальні потужності то така задача вирішиться.!!! Тому пошук дійсно односторонніх функцій чи навіть доказ їх існування є одним з важливих завдань криптографії.
Як приклад односторонньої функції може виступати наступна схема ідентифікації:
- Абонент А виробляє наступну послідовність: x0, f (x0)= x1,..., f (x99)= x100.
- Потім x100 передається по таємному каналу абоненту В.
- Коли А необхідно ідентифікувати себе, він передає по відкритому каналу В x99. Абонент В перевіряє f(x99)=? x100.
- Наступного разу А передасть x99 і В перевірить f (x98)=? x99 і так далі. Перехват повідомлень на i -ому етапі нічого не дасть зловмиснику, так як він не зможе отримати відповідне значення xi-1 (через використання односторонньої функції), щоб наступного разу ідентифікувати себе як абонента А. Дану схему можна представити наступним чином (див. мал. 4-1):
Такі схеми застосовуються для ідентифікації „свій/чужий”.
Односторонньою функцією з секретом (trapdoor one way function) називають функцію fk здійснюючи відображення X  Y, де X та Y – довільні множин, що задовольняють наступним умовам:
Y, де X та Y – довільні множин, що задовольняють наступним умовам:
-
 x
x  X (області визначення) легко обчислити y=fk(x), y
X (області визначення) легко обчислити y=fk(x), y  Y.
Y. - При відомому k
 y
y  Y легко обчислити x=fk -1(y), x
Y легко обчислити x=fk -1(y), x  X.
X. -

Майже для всіх k і майже для всіх y знайти x = fk -1(y) неможливо без знання параметра k.Мал. 4‑ 1
Власне на односторонніх функціях з секретом і будуються асиметричні криптосистеми. Так алгоритм зашифровування з відкритим ключем можна розглядати як односторонню функцію з секретом, а секретом для даної функції є таємний ключ, використовуючи який можна розшифрувати повідомлення. В якості прикладу такої функції можна привести модульну експоненту, що використовується в криптосистемі RSA.