
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание №4.
|
|
Часть II
Раздел 3.
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Контрольные задания
Задание №1. Найти наибольшее и наименьшее значения функции f(x) на отрезке [a; b].
| 1.1. f(x)=x4-x2+5; [-2; 2] | 1.2. f(x)=x+2  ; [0; 4] ; [0; 4]
|
| 1.3. f(x)=x5-5x4+5x3; [-1; 2] | 1.4. f(x)=x3-3x2+6x; [-1; 1] |
| 1.5. f(x)=x4-8x2+3; [-2; 2] | 1.6. f(x)=(x3/3)-2x2+2; [-1; 2] |
| 1.7. f(x)=x3-1, 5x2-6x+1; [-2; 0] | 1.8. f(x)=x4-8x2-8; [-1; 3] |
| 1.9. f(x)=x3-6x2+9x; [-1; 4] | 1.10. f(x)=3x-x3; [-2; 3] |
| 1.11. f(x)=x3-12x+7; [0; 3] | 1.12. f(x)=x5-(5/3)x3+2; [0; 2] |
1.13. f(x)=  x+cosx; [0; p/2] x+cosx; [0; p/2]
| 1.14. f(x)=3x4-16x3+2; [-3; 1] |
| 1.15. f(x)=x3-3x+1; [1/2; 2] | 1.16. f(x)=x4+4x; [-2; 2] |
1.17. f(x)=  x-sinx; [0; p/2] x-sinx; [0; p/2]
| 1.18. f(x)=81x-x4; [-1; 4] |
| 1.19. f(x)=3-2x2; [-1; 3] | 1.20. f(x)=x-sinx; [-p; p] |
1.21. f(x)=x-4  ; [0; 9] ; [0; 9]
| 1.22. f(x)=x5+x4-3x3; [-1; 2] |
| 1.23. f(x)=x-2sinx; [0; p/2] | 1.24. f(x)=(x3/3)-4x-1; [-3; 1] |
Задание №2. Провести полное исследование и построить график функции.
2.1. 
| 2.2. 
|
2.3. 
| 2.4. 
|
2.5. 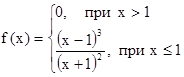
| 2.6. 
|
2.7. 
| 2.8. 
|
2.9. 
| 2.10. 
|
2.11. 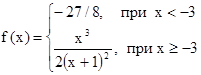
| 2.12. 
|
2.13. 
| 2.14. 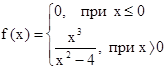
|
2.15. 
| 2.16. 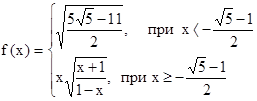
|
2.17. 
| 2.18. 
|
2.19. 
| 2.20. 
|
2.21. 
| 2.22. 
|
2.23. 
| 2.24. 
|
Задание №3. Провести полное исследование и построить график функции.
| 3.1. y=ln(x)/x | 3.2. y=(2x+1)e-x |
| 3.3. y=xex | 3.4. (1/2)ln((x+1)/(x-1)) |
| 3.5. (1/2)ln((1+x)/(1-x)) | 3.6. y=xe-x |
| 3.7. y=x/lnx | 3.8. y= 
|
| 3.9. y=x3e-x | 3.10. y=x-ln(x+1) |
| 3.11. y=(x2-1)/(x2+1) | 3.12. y=x2/(x-1) |
| 3.13. y=(4x3+5)/x | 3.14. y=x4/(x3-1) |
| 3.15. y=(2-4x2)/(1-4x2) | 3.16. y= 
|
| 3.17. y=x2-2lnx | 3.18. y=e1/(2-x) |
3.19. y=(2+x2) 
| 3.20. y=(x-1)e3x+1 |
| 3.21. у=х2е-х | 3.22. у= 
|
| 3.23. у=(3х-2)е1-х | 3.24. y=(x+2)2/(x+1) |
Задание №4.
1) Вычислить приближенно значение функции z=f(x, y) в точке В, исходя из значения функции в точке А и заменив приращение функции дифференциалом.
2) Составить уравнение касательной плоскости к поверхности z=f(x, y) в точке А.
| 4.1. z=x2+xy+y2; A(1; 2); В(1, 02; 1, 96). | 4.2. z=3x2-xy+x+y; A(1; 2); В(1, 02; 1, 96). |
| 4.3. z=x2+3xy-6y; A(4; 1); В(3, 96; 1, 03). | 4.4. z=x2-y2+6x+3y; A(2; 3); В(2, 02; 2, 97). |
| 4.5. z=x2+2xy+3y2; A(2; 1); В(1, 96; 1, 04). | 4.6. z=x2+y2+2x+y-1; A(2; 4); В(1, 98; 3, 91). |
| 4.7. z=3x2+2y2-xy; A(-1; 3); В(-0, 98; 2, 97). | 4.8. z=x2-y2+5x+4y; A(3; 3); В(3, 02; 2, 98). |
| 4.9. z=2xy+3y2-5x; A(3; 4); В(3, 04; 3, 95). | 4.10. z=xy+2y2-2x; A(1; 2); В(0, 97; 2, 03). |
| 4.11. z=x2+xy+y2; A(2; 1); В(2, 02;, 97). | 4.12. z=2x2+3xy+y2; A(2; 2); В(2, 03; 1, 96). |
| 4.13. z=5x2+6xy+x; A(1; 2); В(0, 98; 2, 02). | 4.14. z=3x2+2xy+y2; A(-1; 2); В(-1, 01; 2, 03). |
| 4.15. z=x2+3y2+x-2y; A(1; 2); В(1, 03; 1, 97). | 4.16. z=x2+ y2+xy; A(1; 3); В(1, 07; 2, 93). |
| 4.17. z=x2+2y2+x-y; A(3; 1); В(2, 96; 1, 04). | 4.18. z=x2+3xy+y2-x; A(2; 3); В(2, 03; 2, 98). |
| 4.19. z=x2+2xy-2y2+4x; A(2; 1); В(1, 96; 1, 03). | 4.20. z=x2+xy+y2-x+2y; A(1; 3); В(1, 04; 3, 05). |
4.21.  ; A(3; 4); В(2, 9; 4, 2). ; A(3; 4); В(2, 9; 4, 2).
| 4.22. z=x2-6xy-y2; A(0; -2); В(-0, 1; -1, 9). |
| 4.23. z=5x2-2xy-3y3; A(-2; 1); В(-1, 9; 0, 9). | 4.24.  ; A(4; 1); В(3, 9; 1, 05). ; A(4; 1); В(3, 9; 1, 05).
|
Задание №5. Найти наименьшее и наибольшее значения функции z=f(x, y) в замкнутой области D, заданной системой неравенств. Сделать чертеж области.
5.1. z=x2+y2-9xy+2; 
| 5.2. z=x2+2y2; 
|
5.3. z=-x2-y2-xy+3; 
| 5.4. z=x2+3y2+x-y; 
|
5.5. z=x2+2y2+2xy; 
| 5.6. z=-x2-y2-xy+3; 
|
5.7. z=-x2+2xy+10; 
| 5.8. z=x2-y2+2xy+4x; 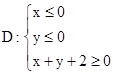
|
5.9. z=x2+xy-2; 
| 5.10. z=x2+xy; 
|
5.11. z=x2-2y2+4xy-6x-1; 
| 5.12. z=x2+y3-3xy; 
|
5.13. z=x2+y2-xy-4x; 
| 5.14. z=x+y+xy; 
|
5.15. z=2x3+y2+4x2-2xy; 
| 5.16. z=x2+y2-xy-4x; 
|
5.17. z=y2-2x+xy; 
| 5.18. z=2xy+y2-4x; 
|
5.19. z=x2+y2+2x+4y+1; 
| 5.20. z=2x2+2y2+2xy; 
|
5.21. z=x2-y2+2xy-8x; 
| 5.22. z=x2+y2-4x; 
|
5.23. z=2xy-y2-x; 
| 5.24. z=x2+2y2+2xy+2x; 
|
Задание №6. Найти уравнение касательной, нормальной плоскости и кривизну линии r=r(t) в точке t0.
6.1. 
|
6.2. 
|
6.3. 
|
6.4. 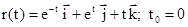
|
6.5. 
|
6.6. 
|
6.7. 
|
6.8. 
|
6.9. 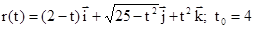
|
6.10. 
|
6.11. 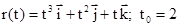
|
6.12. 
|
6.13. 
|
6.14. 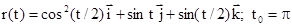
|
6.15. 
|
6.16. 
|
6.17. 
|
6.18. 
|
6.19. 
|
6.20. 
|
6.21. 
|
6.22. 
|
6.23. 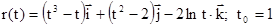
|
6.24. 
|