Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Электр тогының қуаты мен жұмысы
|
|
Уақ ыт бірлігі ішіндегі электр тогының істеген жұ мысы қ уат деп аталады.
P =A/ t (6.40) Тұ рақ ты ток кү ші мынағ ан тең І = q/t болады. Тасымал-
данатын заряд q=І t, мұ ндағ ы t – токтың ө тетін уақ ыты. Бұ л кездегі істелген жұ мыс:
A =qU =ІUt
яғ ни электр тогының жұ мысы токтың кү шіне, бө ліктегі кернеудің тү суіне жә не уақ ытқ а байланысты. Бұ л жұ мыс электрондардың бағ ытталғ анқ озғ алысының кинетикалық энергиясын иондарғ а берілуіне байланысты ө ткізгішті қ ыздыруғ а жұ мсалады, яғ ни А12=Q. Сондық тан, Q = I2Rt, Q = R t жұ мыс пен жылудың ө лшем бірлігі джоуль: 1 Дж = 1А1В1с. ток қ уаты P келесі формуламен есептеледі:
P = IU = I2R = U2.БХЖ-да қ уаттың ө лшем бірлігі ватт: 1Вт= 1А1В.
Тармақ талғ ан тізбектерге арналғ ан Кирхгоф ережелері (67-сұ рақ)
Кү рделі, тармақ талғ ан тізбектердегі токты есептеу ү шін Кирхгоф екі ереже ұ сынды. Тармақ талғ ан тізбек ү шін Кирхгофтың бірінші ережесі: тү йінде (ү штен кем емес ө тгізгіштер тү йісетін нү ктеде) тү йіскен ток кү штерінің алгебралық қ осындысы нө лге тең болады. Шартты тү рде тү йінге бағ ытталғ ан токтар - оң, одан шық қ ан - теріс деп алынады. Тұ рақ ты ток тізбегіндегі тү йінде зарядтардың жиналуы немесе азаюы мү мкін емес деген қ орытындығ а келеміз. Кирхгофтың бірінші ережесінің ө рнегі былай болады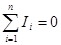 
,
мұ ндағ ы n- тү йінде тоғ ысатын ток саны. 15.1 -суретте кө рсетілген А тү йіні ү шін (15.6) ереже былай жазылады:
I1 – I2 + I3 - I4 + I5 = 0.
Кирхгофтың екінші ережесі тұ йық тізбекке қ олданылады да, ол былай айтылады: электр тізбегінің кез келген тұ йық контурындағ ы ток кү ші мен кедергінің кө бейтінділерінің алгебралық қ осындысы осы контурдағ ы электрқ озғ аушы кү штердің алгебралық қ осындысына тең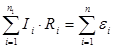 
,
мұ ндағ ы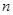 
- контурдағ ы тізбек бө ліктерінің саны. Бұ л ережені қ олданғ ан кезде контурдағ ы токтың оң бағ ытын таң дап алу керек. Токтың бағ ыты таң далғ ан бағ ытпен сә йкес келсе, оң деп алынады. Электрқ озғ аушы кү шінің бағ ыты да токтың оң бағ ытымен сә йкестендіріледі. Кирхгофтың екінші ережесіне мысал ретінде, 15.2-суреттегі тізбекті қ арастырайық. Контур тұ йық жә не ү ш бө ліктен тұ рады. Контурдағ ы токтың оң бағ ытын сағ ат тілі бағ ытымен сә йкес таң дап алайық. Онда ө рнекке сә йкес келесі тең деу орынды болады:
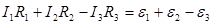
Термодинамикның бірінші бастамасы (35-сұ рақ)
Термодинамиканың бірінші бастамасы энергияның сақ талу жә не тү рлену заң дарын сипаттайды.
Ішкі энергия жү йедегі барлық микробө лшектердің – атомдар мен молекулалардың қ озғ алыс энергияларынан жә не олардың ө зара ә серлесу энергияларынан қ ұ ралады.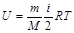 
Тепе-тең дік процесс кезінде газдың кө лемі ө згергенде жасалатын элементар жұ мыс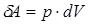 
1-заң ы. Жү йеге берілген жылу мө лшері оның ішкі энергиясының ө згерісі мен жү йенің сыртқ ы кү штерге қ арсы жасайтын жұ мысына жұ мсалады:
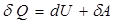. Бірінші текті мә ң гі қ озғ алтқ ыш жасау мү мкін еместігін дә лелдейтін бұ л тұ жырымдама термодинамиканың бірінші заң ы деп аталады.
Физикалық маятник (48-сұ рақ)
Физикалық маятник – С масса центрінен тыс жатқ ан 0 нү ктесі арқ ылы ө тетін горизонталь ө стің айналасында ауырлық кү ші ә серінен тербеліс жасайтын қ атты дене.
Тербеліс параметрлері:;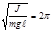 
,
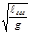мұ ндағ ы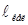 
- физикалық маятниктің келтірілген ұ зындығ ы деп аталады: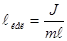 
Элементар электр заряды. Электр заsрядының сақ талу заң ы (50-сұ рақ)
Тыныштық тағ ы зарядтардың физикасын қ арастыратын электр бө лімін электрстатика деп атайды. Табиғ атта электр зарядтары оң жә не теріс болып екі тү рге бө лінеді. Аттас зарядтар тебіледі, ал ә р аттас зарядтар тартылады. Электрон мен протон массалары сә йкесінше: 9, 1× 10-31кг жә не 1, 67× 10-27кг. 3 арядтың сақ талу заң ы анық талғ ан: оқ шауланғ ан жү йеде зарядтардың (оң жә не теріс) алгебралық қ осындысы тұ рақ ты болып қ алады. Оқ шауланғ ан немесе тұ йық жү йе деп сыртқ ы денелермен заряд алмаспайтын жү йені айтады. H ү ктелік заряд дегеніміз – сызық тық ө лшемдері ә серлесуші зарядталғ ан денелердің ара қ ашық тығ ынан ө те аз болып келетін денеде орналасқ ан заряд. Кулон заң ы бойынша: вакуумда орналасқ ан екі 
жә не 
нү ктелік зарядтардың ө зара ә серлесу кү шінің модулі олардың шамаларының кө бейтіндісіне тура, ал ара қ ашық тығ ының квадратына кері пропорционал: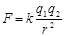 
мұ ндағ ы 
-ө лшем жү йесіне байланысты болатын пропорционалдық коэфффициент.
Энергия, кү ш жұ мысы, қ уат (8-сұ рақ)
Энергия – ә р тү рлі қ озғ алыс кезіндегі материяның кү йін сипаттайтын шама. Материяның ә р тү рлі қ озғ алысымен ә р тү рлі энергияларды байланыстырады. Олар: механикалық, жылулық, электромагниттік жә не т.б. Дененің механикалық қ озғ алысының ө згерісі, сонымен қ атар осы қ озғ алыстың энергиясы, оғ ан ә сер ететін басқ а денелер кү шінің ә серінен болады. Осы кү штер жұ мыс атқ арады.
Кү ш жұ мысы қ озғ алыстың берілу шамасымен немесе бір денеден екінші денеге ө тетін энергия шамасымен сипатталады.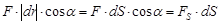 
, 
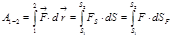Жұ мыс жасайтын кү штер екіге бө лінеді: консервативті жә не консервативті емес. Егер кү штің жұ мысы дененің бастапқ ы жә не соң ғ ы кү йімен ғ ана анық талатын болса, яғ ни оның траекториясына тә уелді болмаса, мұ ндай кү штерді к онсервативті (потенциалды) деп атайды, олар ү шін жұ мыс ә р тү рлі жолдарда бірдей болады.
Атқ арылғ ан жұ мыстың жылдамдығ ын сипаттау ү шін Қ УАТ деген ұ ғ ым енгіземіз:
.
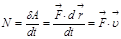Электрстатикалық ө ріс кернеулігі. Кү ш сызық тары (52-сұ рақ)
Ө ріс тарапынан ә сер етуші кү штің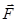 
ө ріске енгізілген зарядтың шамасына 
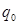қ атынасын электр ө рісінің кернеулігі деп атайды: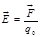 
.
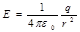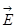векторының циркуляциясы теоремасынан бірнеше маң ызды қ орытындылар шығ аруғ а болады:
1) электрстатикалық ө ріс 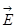кернеулігінің кү ш сызық тары тұ йық болуы мү мкін емес
2) 12.2-суретте кө рсетілген тү рдегі электрстатикалық ө рістің болуы мү мкін емес.
Электрстатикалық ө рістің кү ш сызық тары тұ йық талғ ан болуы мү мкін емес
Электростатикалық ө ріс кернеулік векторының циркуляциясы. Электростатикалық ө рістің потенциалдылық шарты(55-сұ рақ)
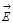векторының циркуляциясы теоремасынан бірнеше маң ызды қ орытындылар шығ аруғ а болады:
1) электрстатикалық ө ріс 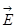кернеулігінің кү ш сызық тары тұ йық болуы мү мкін емес
Шындығ ында да, егер 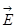векторының қ андай да бір сызығ ы тұ йық болса, онда осы сызық бойымен 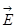векторының циркуляциясын алсақ
теориямен қ арама-қ айшылық қ а келуші едік. Узік-ү зік сызық тарғ а 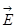векторының циркуляциясы теоремасын қ олданса, онда ол нө лден ерекше болады, ал ол теоремағ а қ арама-қ айшы келеді.
Электростатикалық ө ріс потенциалы. Потенциалдар айырымы. Эквипотенциалдық беттер(56-сұ рақ)
Электрстатикалық ө ріс потенциалы. Потенциалдық ө рістегі консервативтік кү штер жұ мысы потенциалдық энергияның кемуі нә тижесінде істелетінін ескере отырады: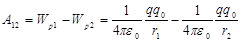 
ө рістің потенциалы деп атайды: 
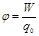Зарядты ө рістің бір нү ктесінен оның екінші нү ктесіне дейін орын ауыстырғ анда істелетін жұ мысты тең дігін ескере отырып, тө мендегідей тү рде жазуғ а болады: 
. 
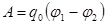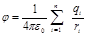
Электрстатикалық ө рісті графиктік тү рде кү ш сызық тары арқ ылы ғ ана емес эквипотенциалды беттер арқ ылы да кескіндеуге болады. Эквипотенциалдық беттер деп барлық нү ктелерінің потенциалдары бірдей беттерді айтады. Егер ө рісті нү ктелік заряд тудырса, онда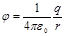 
формуласына сә йкес эквипотенциалдық беттер сфера тү рінде болады
Энтропия. Клаузиус тең сіздігі (40-сұ рақ)
Жү йенің қ андай да бір денеден алғ ан жылу мө лшерінің сол дененің температурасына қ атынасын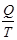 
, Клаузиус, келірілген жылу мө лшері деп атады. Оның физикалық мағ ынасы: жү йенің циклде сырттан алғ ан келтірілген жылуының элементар мө лшерлерінің қ осындысы қ айтымды циклдер ү шін нө лге тең, ал қ айтымсыз циклдер ү шін нө лден кіші болады: 
.
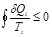Энтропия (гр. еntropіa – бұ рылыс, айналу) – тұ йық термодинамикалық жү йедегі ө здігінен жү ретін процестің ө ту бағ ытын сипаттайтын кү й функциясы. Энтропияның кү й функциясы екендігі термодинамиканың екінші бастамасында тұ жырымдалады. Энтропия ұ ғ ымын термодинамикағ а 1865 ж. Р.Клаузиус енгізген.
1) Энтропияның ө згеру сипаты бойынша жылуалмасу процесінің бағ ытын анық тауғ а болады.
2) Оқ шауланғ ан жү йенің э нтропиясы қ айтымсыз процестер кезінде тек қ ана ө седі, қ айтымды процестер кезінде тұ рақ ты болып қ алады. Олай болса, оқ шауланғ ан термодинамикалық жү йенің энтропиясы ешқ ашан кемімейді: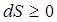 
.
3) Қ айтымды адиабаттық процестер изоэнтропты (мұ ндай процестерде энтропия ө згермейді)болады.
5) Жү йенің байланысқ ан энергиясы.
6) Энтропия – термодинамикалық жү йедегі кү йлер ық тималдылығ ының ө лшемі
Электростатикалық ө ріс кернеулігі мен потенциалы арасындағ ы байланыс(57-сұ рақ)
O рын ауыстырғ анда Iстелінетін жұ мыс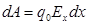 
болсын. Екіншіден, бұ л жұ мыс 
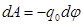болады. Tең естіргенде: 
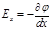Дә л осылай 
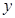жә не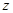 
ө стерін қ арастыра отырып, 
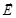векторының тө мендегідей ө рнегіне келеміз 
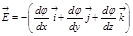мұ ндағ ы 
- 
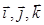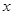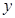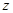, , – координат осьтері бойымен бағ ытталғ ан бірлік векторлар.
Электрстатикалық ө рістегі диэлектриктер (58-сұ рақ)
Диэлектриктердің атомдары мен молекулалары тұ тас алғ анда бейтарап болады, ө йткені қ ұ рамындағ ы микроскопиялық теріс жә не оң зарядтардың мө лшерлері бірдей. Қ ұ рылымына қ арай
Ү шке бө лінеді:
Бірінші топқ а жататын диэлектриктердің оң жә не теріс зарядтарының ауырлық центрлері бір-біріне сә йкес келеді. Мысалы, парафин, бензол, азот, газтә різдес сутегі, кө мірсутектілердің қ атары. Мұ ндай диэлектриктер молекулаларының сыртқ ы ө ріс жоқ кезде дипольдік моменті болмайды. Сондық тан мұ ндай диэлектриктердің молекулалары – полярлы емес деп аталады. Сыртқ ы электр ө рісінде молекулалардың оң жә не теріс зарядтарының ² ауырлық центрі² қ арама-қ арсы ығ ысады, ол аралық 
молекулалардың ө лшемімен салыстырғ анда аз болады. Бұ л кезде ә р молекула: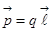 
дипольдік моментке ие болады.
Екінші топқ а – су, нитробензол, т.с.с. молекулаларының қ ұ рылысы асимметриялы заттар жатады. Бұ ларда сыртқ ы ө ріс жоқ кезде де, оң жә не теріс иондардың ² ауырлық центрі² бір-бірімен сә йкес келмейтіндіктен, сондық тан олар ² қ атаң ² диполь қ ұ райды. Мұ ндай полярлы молекулалардың дипольдік моментінің сан мә ні: 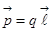=10-19 Кл∙ 10-10м=10-29 Кл × м шамасындай болады
Ү шінші топқ а иондық қ ұ рылымы бар кристалдық диэлектриктер жатады (хлорлы натрий, хлорлы калий т.с.с). Бұ ларды электр ө рісіне енгізгенде кристалл торының оң иондарының ө рістің бағ ытымен, теріс иондарының ө ріске қ арсы бағ ытпен біршама ығ ысуы болады. Мұ ндай диэлектриктерде жалпы алғ анда сыртқ ы ө ріске пропорционал ө ріс бойымен бағ ытталғ ан дипольдік момент болады.