
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Винтовые поверхности с криволинейной образующей
|
|
2. Винтовые поверхности с прямолинейной образующей и направляющей – винтовой линией постоянного шага
3.4.1 Винтовые поверхности с криволинейной образующей
Винтовая поверхность, образованная плоской кривой а, совершающей винтовое перемещение в пространстве, представлена в соответствии с рисунком 59.

Рисунок 59
Кривая а пересекает винтовую линию m (А, А1, А2 … Аn) и касается поверхности α в некоторых точках (В, В1, В2, … Вn).
3.4.2 Винтовые поверхности с прямолинейной образующей и направляющей – винтовой линией постоянного шага Характерной особенностью для винтовых поверхностей с постоянным шагом является постоянство угла ϕ - угла наклона прямолинейной образующей к направляющей плоскости (плоскости, перпендикулярной оси винтовой поверхности). Все точки образующей при винтовом движении описывают винтовые линии, каждая из которых может служить направляющей поверхности. Такие линии называют винтовымипараллелями. Все винтовые параллели имеют одинаковый шаг Р, называемый шагом винтовой поверхности, в соответствии с рисунком 60. Для получения наглядного изображения винтовой поверхности задают проекции геометрической части определителя – образующей, направляющих
с каркасом, состоящих из двух семейств линий (винтовых параллелей и прямолинейных образующих). Линейчатые винтовые поверхности называют
геликоидами, если угол наклона образующей к оси поверхности равен 900, в
этом случае геликоид называется прямым. При произвольном угле наклона,
отличным от 00 и 900 геликоид называют косым (наклонным).
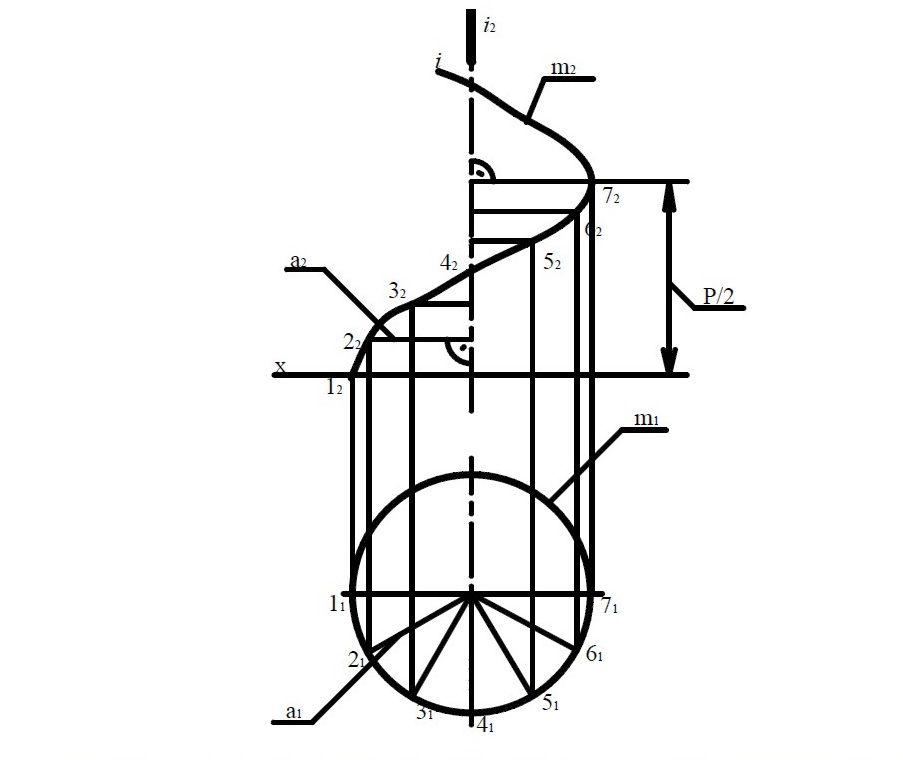
Рисунок 60
На рисунке 60 изображен прямой геликоид в виде отсека, заключенного между направляющей m и осью i. Закон образования состоит из: образующая а (а1, а2) пересекает направляющую m, ось i, а ⊥ i. Косой геликоид (в виде отсека) строится с помощью конуса (1 2) β β β в соответствии с рисунком 61.
Образующие lA, lB, lC … и т.д. проводятся параллельно образующим S1, S2, S3 … и т.д. направляющего конуса β: l2A // S212, l2B // S222, l2C // S232 …
и т.д. и пересекают ось i. Прямые и косые геликоиды подразделяются на закрытые и открытые. Если образующая и ось пересекаются, геликоид называют закрытым (Рисунок 60, 61).

Рисунок 61
Если образующая и ось скрещиваются, геликоид называют открытым,
в соответствии с рисунком 62.

Рисунок 62
Данная поверхность носит название косого кольцевого геликоида, так как образующие l (l1A, l2A, l1B, l2B … и т.д.) скрещиваются с осью
направляющего цилиндра i под углом, отличным от 900. По своему образованию винтовые поверхности, изображенные на рисунках 60, 61, 62 являются коноидами, так как образующая есть прямая линия, она пересекает две направляющие линии, кривую m и прямую i (ось), оставаясь параллельной плоскости, перпендикулярной оси i (рисунок 60), образующим направляющего конуса β (рисунок 61, 62).
Вопросы к аттестации:
1. Что такое поверхность при задании кинематическим способом?
2. Что такое каркас?
3. Что такое очерк поверхности?
4. Что такое определитель?
5. Какая поверхность называется поверхностью вращения?
6. Определите траекторию движения точек линии l при образовании
поверхности вращения?
7. Какая поверхность называется тором?
8. Какая поверхность называется глобоидом?
9. В каком случае образуется однополостный гиперболоид
вращения?
10. Когда точка принадлежит поверхности вращения?
11.Чем пользуются для определения видимости точек поверхности
вращения?
12. Определите образующую линию линейчатой поверхности.
13. Какие поверхности называются линейчатыми?
14. Как образуется прямой цилиндроид?
15. Как образуется прямой коноид?
16. Как образуется поверхность гиперболического параболоида (косой
плоскости)?
17. Как образуется цилиндрическая поверхность?
18. Как образуется коническая поверхность?
19. Что такое эллиптический цилиндр?
20. Как образуется винтовая поверхность?
21. По какому признаку винтовые поверхности подразделяются на
открытые и закрытые?
22. Применение кривой поверхности. Цилиндроид
23. Применение кривой поверхности. Гиперболический параболоид
24. Применение кривой поверхности. Однополый гиперболоид вращения (Зарисовать пример)
25. Применение кривой поверхности. Гиперболический параболоид вращения. (Зарисовать пример)
26. Применение кривой поверхности. Двуполый гиперболоид вращения.
27. Применение поверхности вращения общего вида (Зарисовать пример)
28. Применение сложной поверхности вращения (Комплексный чертеж и пример)
29. Применение поверхности висячих покрытий (Комплексный чертеж и пример)