Показатели безотказности

Вероятностью безотказной работ системы, называется вероятность того, что она будет сохранять свои характеристик в заданных пределах в течение определенного про­межутка времени при определенных условиях эксплуатации. Эта характеристика обозна­чается P(t).

Пусть t — время, в течение которого необходимо определить вероятность безотказной работы, а Т, — наработка до отказа. Тогда, согласно определению вероятности безотказной работы, ее математическое определение будет следующим

P(t) = p(T ≥ t),

т. е. вероятность безотказной работы — это вероятность того, что наработка до отказа Т будет больше или равно времени t, в течение которого определяется вероятность безотказной работы.

Из определения вероятности безотказной работы видно, что эта характеристика имеет следующие свойства:

1) P(t) является убывающей функцией времени. Типичная зави­симость P(t) приведена на рис.

2) 0 ≤ P(t) ≤ 1

3) Р(0) = 1, Р(∞) = 0.

На практике для определения P(t) часто пользуютсястатистическим определением

где N₀ – число образцов поставленных на испытание; N – число исправно работающих образцов к моменту времени t; n(t) – число отказавших образцов за время t.

График вероятности безотказной работы полученный на основании статистических данных пред­ставляет собой ступенчатую линию со скачками, кратными 1/N₀ в моменты отказов.

При увеличении числа образ­цов N₀ статистическая оценка Р* (t) вероятности обнаруживает устой­чивость, т. е. Р* (t) слабо отличается от вероятности безотказной работы P(t) полученной на основе математической модели:

P(t) ≈ P^*(t)

На практике иногда более удобной характеристикой является ве­роятность неисправной работы, или вероятность отказа. Исправная работа и отказ являются событиями несовместными и противоположными, поэтому вероятность безотказной работы и вероятность отказа Q (f) связаны зависимостью

Q(t) = 1 - P(t)

Тогда математическое определение:

Q(t) = p(T ≤ t),

Вероятность отказа Q(t) – это вероятность того, что случай­ное время до отказа T меньше заданного времени t.

Типичный график зависимости Q(t) представлен на рис.

Из определения вероятности отказа видно, что этот показатель является функцией распределения времени наработки до отказа Т, т. е.,

Q(t) = F(t)

Функция распределения F(x), равна вероятности того, что случайная величина Х принимает значение не превышающее х.

Статистическое определение вероятности отказа:

График Q^*(t), как и P^*(t) пред­ставляет собой ступенчатую линию со скачками, кратными 1/N₀ в моменты отказов.

Частота отказов. Частотой отказов f(t) называется отношение числа отказавших образцов в единицу времени к числу образцов, первоначально установленных на испытание при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными.

Согласно определению:

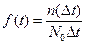- статистическое определение

где n(∆ t) – число отказавших образцов в интервале времени от t - ∆ t/2 до t + ∆ t/2; ∆ t – интервал времени.

Математическое определение:

Из этого выражения видно, что частота отказов есть плотность распределения времени работы системы до ее отказа.

Так как Q(t) = F(t) то,

Интенсивность отказов. Интенсивностью отказов λ (t) называется отношение числа отка­завших образцов в единицу времени к среднему числу образцов, исправно работающих в данный отрезок времени при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными.

Согласно определению

где N_ср – средние число исправно работающих изделий в интервале ∆ t.

где N_i – число исправно работающих образцов в начале интервала ∆ t; N_i+1 – число исправно работающих образцов в конце интервала ∆ t.

Типичная кривая изменения ин­тенсивности отказов аппаратуры во времени приведена на рис. Из кривой видно, что в работе аппаратуры можно выделить три
характерных участка. На участке от 0 до t₁ интенсивность отказов резко уменьшается. Высокая интенсивность отказов на начальном участке объясняется наличием большого числа отказов вначале эксплуатации из-за элементов, имеющих внутренние дефекты, ошибок производства, неопытности обслуживающего персонала и т. п. Этот участок называется обычно периодом приработки элементов. Участок приработки в процессе эксплуатации аппаратуры может отсутствовать. Это имеет место в том случае, когда на заводе-изготовителе произведена тщательная отбраковка элементов с внутренними дефектами и осуще­ствлена приработка аппаратуры в процессе ее испытания.

На участке от t₁ до t₂ интенсивность отказов постоянна. Этот участок характеризует нормальную работу системы и является несоизмеримо более длинным, чем участок приработки. Именно этот участок соответствует основному времени эксплуатации систем. Старение на этом участке отсутствует.

Участок от t₂ до t₃ характеризуется резким ростом интенсивности от­казов, что объясняется механическим и электрическим износом эле­ментов. Этот участок называется к периоду старения системы.

Обычно аппаратуру не эксплуатируют до состояния износа. Ее ремонтируют, износившиеся элементы заменяют новыми, после чего частота отказов аппаратуры вновь соответствует участку времени от t₁ до t₂. Поэтому изучение поведения системы на участ­ке t > t₃ не является предметом теории надежности.

Математическое определение интенсивности отказов:

Среднее время безотказной работы T_ср выражается как матема­тическое ожидание времени безотказной работы:

Статистическое определение:

где N₀ - поставленное на эксперимент количество изделий, t_i - время до отказа изделия.

Из формулы видно, что для определения Т_ср необходимо знать моменты отказов всех образцов аппаратуры, над которыми проводится эксперимент. При большом числе образцов N₀ это может сильно усложнить эксперимент. Поэтому иногда удобно вычислять Т_ср по формуле

где n_i – число образцов, отказавших в i-м интервале, t_{ср i} = (t_i-1 + t_i)/2 – среднее время i-го интервала, t_i-1 – время в начале i-го интервала, t_i - время в конце i-го интервала, t_k – время, в течение которого отказали все N₀ образцов, ∆ t – выбранная величина интервала времени.

Вычисления Т_ср по статистическим формулам тем точнее, чем больше число образцов N₀.

С вероятностью безотказной работы среднее время безотказной работы связано следующим выражением:

Последнее уравнение может быть представлено как выражение площади под кривой P(t) (рис.). Время безотказной работы T_ср может быть оценено как ширина прямоугольника единичной высоты, по площади равного площади под кривой P(t).

Среднее время безотказной работы является естественным показателем надежности, однако оно не говорит ничего о характере распределения времени до отказа. Например, две совершенно различные функции P₁(t) и P₂(t), выра­жающие резко отличающиеся вероятности безотказной работы могут характеризоваться одинаковыми зна­чениями T_ср. Чтобы различать такие случаи, наряду с показателем T_ср применяется показатель среднеквадратическое отклонение времени безотказной работы σ _t или его квадрат дисперсия D_t.

Дисперсия характеризует величину разброса времени до отказа относительно среднего значения.

Показатели σ _t и D_t можно определять также статистически, по формуле