
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие непрерывности функции в точке
|
|
Лекция
Понятие непрерывности функции в точке, а затем на промежутке Х рассматривается в связи с тем, что именно для таких функций изучаются правила нахождения промежутков монотонности, точек экстремума, наибольшего и наименьшего значений.
Рассмотрим один из возможных подходов к введению понятия функции, непрерывной в точке.
Учащимся предлагаются графики функций (с. 2), и задаётся вопрос: «На каких рисунках данные функции непрерывны в указанных точках, то есть графики каких функций могут быть построены, не отрывая карандаша»?
Ответ: 1, 5, 6.
Чтобы выявить, какими свойствами обладают указанные функции и не обладают остальные, ответим на следующие вопросы.
1, Определена ли данная функция в указанной точке?
2. Имеет ли она предел в этой точке?
3. Равен ли предел значению?
Делаем выводы.
Вводим определение. Функция называется непрерывной в точке х0, если верно равенство 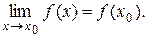
Замечание. Говоря о непрерывности функции в точке, будем рассматривать только внутренние точки области определения, так как понятие предела функции также было рассмотрено только для внутренних точек области определения. Например, на рис. 6 х = 0 не является внутренней точкой. Поэтому мы не будем рассматривать непрерывность функции  в этой точке.
в этой точке.
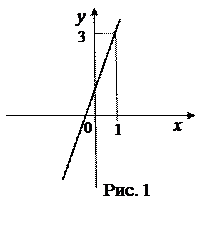 1)
1) 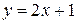 , х = 1. 2)
, х = 1. 2)  3)
3) 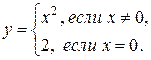



 4)
4)  5)
5)  6)
6) 

Далее учащимся могут быть предложены графики функций, для которых следует ответить на вопрос: «Какое условие определения непрерывности функции в точке не выполнено на рис. 2 - 4?»
Ценность введённого определения состоит в том, что оно подменяет вычисление предела функции в точке вычислением её значения.
В учебнике Мордковича А.Г. приводится утверждение «если выражение f (x) составлено из рациональных, иррациональных, тригонометрических... выражений, то функция у = f (x) непрерывна в любой точке, в которой определено выражение f (x)» со ссылкой на то, что математики доказали.
Пример 1.
Вычислить:  . Ответ: 7.
. Ответ: 7.
Пример 2.
Вычислить: 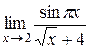 .
. 

Пример 3.
Вернёмся к примеру 2, который мы использовали при введение предела функции в точке. По графику очевидно, что 
Вычислить: 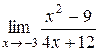 .
.

Наконец определим функцию, непрерывную на промежутке Х.
Функцию  называют непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.
называют непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.