
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Схемы синтаксически управляемого перевода
|
|
Определение. Cхемой синтаксически управляемого перевода (или трансляции, сокращенно: СУ-схемой) называется пятерка  , где
, где
(1) N - конечное множество нетерминальных символов;
(2) T - конечный входной алфавит;
 - конечный выходной алфавит;
- конечный выходной алфавит;
R - конечное множество правил перевода вида
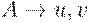
где  и вхождения нетерминалов в цепочку v образуют перестановку вхождений нетерминалов в цепочку u, так что каждому вхождению нетерминала B в цепочку u соответствует некоторое вхождение этого же нетерминала в цепочку v; если нетерминал B встречается более одного раза, для указания соответствия используются верхние целочисленные индексы;
и вхождения нетерминалов в цепочку v образуют перестановку вхождений нетерминалов в цепочку u, так что каждому вхождению нетерминала B в цепочку u соответствует некоторое вхождение этого же нетерминала в цепочку v; если нетерминал B встречается более одного раза, для указания соответствия используются верхние целочисленные индексы;
(5) S - начальный символ, выделенный нетерминал из N.
Определим выводимую пару в схеме Tr следующим образом:
(1) (S, S) - выводимая пара, в которой символы S соответствуют друг другу;
(2) если (xAy; x'Ay') - выводимая пара, в цепочках которой вхождения A соответствуют друг другу, и A -> u, v - правило изR, то (xuy; x'vy') - выводимая пара. Для обозначения такого вывода одной пары из другой будем пользоваться обозначением  (xAy, x'Ay') => (xuy, x'vy'). Рефлексивно-транзитивное замыкание отношение
(xAy, x'Ay') => (xuy, x'vy'). Рефлексивно-транзитивное замыкание отношение  обозначим => *.
обозначим => *.
Переводом  , определяемым СУ-схемой Tr, назовем множество пар
, определяемым СУ-схемой Tr, назовем множество пар

Если через P обозначить множество входных правил вывода всех правил перевода, то G = (N, T, P, S) будет входной грамматикой для Tr.
СУ-схема  называется простой, если для каждого правила A -> u, v из R соответствующие друг другу вхождения нетерминалов встречаются в u и v в одном и том же порядке.
называется простой, если для каждого правила A -> u, v из R соответствующие друг другу вхождения нетерминалов встречаются в u и v в одном и том же порядке.
Перевод, определяемый простой СУ-схемой, называется простым синтаксически управляемым переводом (простым СУ-переводом).
Пример 5.2. Перевод арифметических выражений в ПОЛИЗ (польскую инверсную запись) можно осуществить простой СУ-схемой с правилами
| E -> E + T | ET+ |
| E -> T | T |
| T -> T * F | TF+ |
| T -> F | F |
| F -> id | id |
| F -> (E) | E. |
Найдем выход схемы для входа id * (id + id). Нетрудно видеть, что существует последовательность шагов вывода

переводящая эту цепочку в цепочку id id id + *.
Рассмотрим связь между переводами, определяемыми СУ- схемами и осуществляемыми МП-преобразователями [2].
Теорема 5.1. Пусть P - МП-преобразователь. Существует такая простая СУ-схема Tr, что  .
.
Теорема 5.2. Пусть Tr - простая СУ-схема. Существует такой МП-преобразователь P, что  .
.
Таким образом, класс переводов, определяемых магазинными преобразователями, совпадает с классом простых СУ-переводов.
Рассмотрим теперь связь между СУ-переводами и детерминированными МП-преобразователями, выполняющими нисходящий или восходящий разбор [2].
Теорема 5.3. Пусть  - простая СУ- схема, входной грамматикой которой служит LL(1)- грамматика. Тогда перевод
- простая СУ- схема, входной грамматикой которой служит LL(1)- грамматика. Тогда перевод  можно осуществить детерминированным МП-преобразователем.
можно осуществить детерминированным МП-преобразователем.
Существуют простые СУ-схемы, имеющие в качестве входных грамматик LR(1)-грамматики и не реализуемые ни на каком ДМП-преобразователе.
Пример 5.3. Рассмотрим простую СУ-схему с правилами
| S -> Sa, | aSa |
| S -> Sb, bSb | bSb |
| S -> e, | e |
Входная грамматика является LR(1)-грамматикой, но не существует ДМП-преобразователя, определяющего перевод 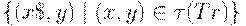 .
.
Назовем СУ-схему  постфиксной, если каждое правило из R имеет вид A -> u, v, где
постфиксной, если каждое правило из R имеет вид A -> u, v, где  . Иными словами, каждый элемент перевода представляет собой цепочку из нетерминалов, за которыми следует цепочка выходных символов.
. Иными словами, каждый элемент перевода представляет собой цепочку из нетерминалов, за которыми следует цепочка выходных символов.
Теорема 5.4. Пусть Tr - простая постфиксная СУ-схема, входная грамматика для которой является LR(1). Тогда перевод
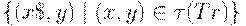
можно осуществить детерминированным МП-преобразователем.