
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пути повышения экономичности режима энергетической системы
|
|
Наибольшая экономичность режима системы должна достигаться в первую очередь за счет повышения экономичности отдельных агрегатов: повышения к.п.д. котлов, улучшения вакуума у паровых турбин, улучшения режима подогрева питательной воды, увеличения полезного напора гидротурбин, правильной установки наклона лопастей гидротурбин.
Не останавливаясь на вопросах экономичности работы отдельных агрегатов при заданной нагрузке, рассматриваемых в специальных работах, посвященных эксплуатации оборудования электростанций, будем в дальнейшем считать, что при данной нагрузке каждый агрегат работает в наиболее экономичном режиме.
Другим не менее важным фактором, определяющим экономичность режима энергетической системы, является наилучшее распределение нагрузок системы между отдельными агрегатами (генераторами, синхронными компенсаторами, котлами, вспомогательным оборудованием электростанций). Основным условием для получения наибольшей экономичности режима системы в целом за счет наилучшего распределения нагрузок (мощностей) является возможность свободного их распределения между отдельными элементами системы. Так, например, при дефиците мощности в отдельные часы все элементы системы должны, быть загружены до предела и свободы распределения нет.
Третьим фактором является наилучший выбор включенных в работу агрегатов электрических станций и сетей. Наличие расхода на холостой ход агрегатов заставляет по экономическим соображениям отключать часть агрегатов электростанций. В различные часы суток наивыгоднейшая комбинация включенных агрегатов изменяется. Кроме того, наличие пусковых затрат на пуск отдельных агрегатов оказывает влияние на выбор включенных агрегатов. В связи с этим оказывается невозможным выбрать наивыгоднейшую комбинацию включенных агрегатов только для данного момента времени, а требуется учесть влияние предыдущего режима на этот выбор, так же как и влияние этого выбора на последующий режим. При наличии определенных требований к величине оптимального резерва мощности выбор наилучшей комбинации включенных агрегатов тесно связан с экономичным распределением резерва мощности.
Метод множителей Лагранжа
В дальнейшем будут рассмотрены наиболее простые задачи и методы распределения нагрузки в ЭЭС. Эти методы используют математический оптимизационный аппарат множителей Лагранжа, который пригоден не ко всем случаям, встречающимся на практике. В частности, он позволяет решать задачу при сепарабельной функции и при ограничениях в форме неравенств только на независимые переменные (например, предельные мощности электростанций) и не позволяет учитывать ограничения в форме неравенств на зависимые переменные (например, пропускные способности ВЛ).
Рассмотрим основные положения метода неопределенных множителей Лагранжа. Пусть имеется целевая функция F (Xl, Х2,..., Хn), экстремум которой определяется. Переменные (Хl, Х2,..., Хn) связаны между собой К уравнениями связи:

Алгоритм расчета при использовании метода множителей Лагранжа заключается в том, что вместо экстремума функции F (Xl, Х2,..., Хn) находятся условия экстремума специально составленной функции (функции Лагранжа), которая включает и целевую функцию, и уравнения связи. Функция Лагранжа при этом имеет вид

а постоянные множители l i называются неопределенными множителями Лагранжа. Дифференцируя функцию по независимым переменным (Xl, Х2,..., Хn) и приравнивая нулю частные производные, находим экстремум.
Для получения минимума Ф нужна для каждого экстремума определить знак второго дифференциала F. Минимуму F соответствует положительный знак второго дифференциала Ф:
d2Ф > 0.
Задача минимизации или максимизации в применении к энергетическим системам и в более широком плане является задачей оптимизации и, в частности задачей оптимизации режима. Под оптимизацией следует понимать определение оптимальных с экономической точки зрения параметров режима энергосистемы. К их числу относятся не только мощности (активные и реактивные) генерирующих источников, но также коэффициенты трансформации, схемы соединений электростанций и электрических сетей, уставки автоматических устройств и т.п. В принципе следует обеспечить комплексную оптимизацию энергосистемы в целом, т. е. комплексно определять оптимальные значения всех указанных выше параметров режима, которые взаимно влияют. К сожалению, техническая сложность оптимизации режима энергосистемы в целом вынуждает пока производить оптимизацию режима «по частям».
Наряду с указанным выше общим методом оптимизации Лагранжа в последнее время начали применяться и другие методы: градиентный метод, метод покоординатного спуска, метод динамического программирования и т.п.
Распределение активной нагрузки между ТЭС
Рассмотрим очень простую задачу – наивыгоднейшее распределение активной нагрузки с учетом потерь активной мощности в сети, введя следующую систему допущений:
- пусть тепловая энергосистема представляется в виде концентрированной, в которой все станции работают на одну общую нагрузку;
- сеть радиальная;
- напряжения в узлах станций известны и постоянны;
- распределение активных нагрузок не влияет на распределение реактивных.
Задача заключается в том, чтобы найти условия наивыгоднейшего распределения нагрузки между ТЭС с учетом потерь активной мощности в сети.
Будем считать, что система имеет i = 1, 2,..., n тепловых электростанций, для которых известны расходные характеристики Bi (PT i ) и суммарная нагрузка Р н. Для этого случая:
1. Уравнение цели
В = В 1(РТ1) + В 2(РТ2) +... + Вn (P T n ) Þ min.
2. Уравнение связи Вi (РТ i).
3. Ограничения - балансовые уравнения мощности
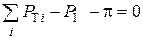
где p - суммарные потери активной мощности.
4. Выведем уравнение оптимизации. Функция Лагранжа
Ф = (В 1 +В 2 +...+ Bn) + l(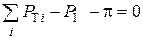 ) = 0.
) = 0.
Так как выражение во вторых скобках равно нулю, то минимумы функции Лагранжа Ф и целевой функции B совпадают.
Дифференцируем функцию Лагранжа по переменным РТ1,..., РТ n и приравниваем производные нулю, тогда

Легко видеть, что

Введем обозначения:
 относительный прирост расхода топлива электростанций, который показывает, как изменится расход топлива i ‑ станции, если ее нагрузка изменится на величину
относительный прирост расхода топлива электростанций, который показывает, как изменится расход топлива i ‑ станции, если ее нагрузка изменится на величину  .
.
 – формула для вычисления относительного прироста потерь активноймощности в сетях, т.е. величина, показывающая, насколько изменятся потери в сетях, если мощность только i -й станции изменится на
– формула для вычисления относительного прироста потерь активноймощности в сетях, т.е. величина, показывающая, насколько изменятся потери в сетях, если мощность только i -й станции изменится на  .
.
Применяя эти обозначения, получаем условия наивыгоднейшего распределения нагрузки:

При выполнении этого условия минимум, а не максимум функции Лагранжа будет только в том случае, если  , т.е.
, т.е. 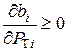 . Это означает, что характеристики относительных приростов электростанций должны быть монотонно возрастающими.
. Это означает, что характеристики относительных приростов электростанций должны быть монотонно возрастающими.
Энергетические характеристики электростанций и агрегатов часто не удовлетворяют указанным условиям. В этом случае они " исправляются" по специальной методике.
Выясним физический смысл условия  . Для этого запишем его в конечных разностях и умножим числитель и знаменатель на DРт, т.е.
. Для этого запишем его в конечных разностях и умножим числитель и знаменатель на DРт, т.е.

Из этого следует, что при наивыгоднейшем распределении нагрузки прирост расхода топлива DВ на прирост активной мощности DРн у потребителя должен быть одинаковым для всех электростанций.
Чтобы учесть потери мощности p даже для простой схемы сети, требуется рассчитать ее установившийся режим, т.е. решить систему уравнения установившегося режима. Для реальных случаев сеть имеет замкнутые контуры, большое число узлов и ветвей и задача расчета ее установившегося режима сложна, причем зачастую она сложнее самой задачи распределения нагрузки. Во многих случаях вводят допущения – потери в сети учитываются приближенно, например, в виде поправок к характеристикам станций.
Наивыгоднейшее распределение нагрузки без учета потерь активной мощности. Такая задача более характерна для распределения нагрузки между агрегатами электростанции, чем для энергосистемы. Однако для энергосистем с высокой степенью концентрации мощности такая постановка также возможна, так как неучет потерь мощности в сетях не приводит к большим погрешностям.
При неучете потерь активной мощности, т.е. при Dp = 0, условие наивыгоднейшего распределения нагрузки имеет вид
bi = idem.
Оптимальный режим соответствует равенству относительных приростов станций.
Полученное условие сохраняется для гидроагрегатов, турбин и котлов ТЭС. Для группы параллельно работающих агрегатов равенство относительных приростов дает минимум целевой функции.
Принцип равенства относительных приростов объясним физически (см. рис.).

Рис. Иллюстрация оптимальности режима при равенстве относительных приростов
Если относительные приросты двух работающих агрегатов, имеющих мощности Р 1 и Р 2и возрастающие характеристики  , не равны, то лучший режим будет у агрегата 1с меньшим относительным приростом. Поскольку этот агрегат экономичнее другого, то его нужно загрузить дополнительно на D Р, соответственно на D Р снизить нагрузку другого, при этом будет получена экономия. Но при загрузке агрегата 1на D Р повышается его относительный прирост до
, не равны, то лучший режим будет у агрегата 1с меньшим относительным приростом. Поскольку этот агрегат экономичнее другого, то его нужно загрузить дополнительно на D Р, соответственно на D Р снизить нагрузку другого, при этом будет получена экономия. Но при загрузке агрегата 1на D Р повышается его относительный прирост до  , а у агрегата 2он снижается до
, а у агрегата 2он снижается до  .Только при равенстве относительных приростов (нагрузки
.Только при равенстве относительных приростов (нагрузки  ,
,  ) дальнейшее перераспределение нагрузки не дает дополнительной экономии, и этот режим, следовательно, оптимальный.
) дальнейшее перераспределение нагрузки не дает дополнительной экономии, и этот режим, следовательно, оптимальный.