
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение моделирующих алгоритмов
|
|
Имитационная модель позволяет исследовать поведение различных систем с учетом влияния случайных факторов. Эти факторы в зависимости от их природы могут быть отражены в модели как случайные события, случайные величины (дискретные или непрерывные), или как случайные функции (процессы).
Например, если с помощью создаваемой имитационной модели предполагается исследовать надежность вычислительной системы, то возникновение отказа будет представлено в модели как случайное событие. Если же модель предназначена для оценки временных параметров процесса обслуживания клиентов в автомастерской, то интервал времени до появления очередного клиента удобнее всего описать как случайную величину, распределенную по некоторому закону [3].
В основе всех методов и приемов моделирования случайных факторов лежит использование случайных чисел, имеющих равномерное распределение на интервале [0; 1].
«Истинно» случайные числа формируются с помощью аналого-цифровых преобразователей на основе сигналов физических генераторов, использующих естественные источники случайных шумов (радиоактивный распад, шумы электронных и полупроводниковых устройств и т.п.).
Случайные числа, генерируемые аппаратно или программно на ЭВМ, называются псевдослучайными. Однако их статистические свойства совпадают со статистическими свойствами «истинно» случайных чисел. В состав практически всех современных систем программирования входят специальные функции генерации случайных чисел, которые обычно называют датчиками, или генераторами, случайных чисел.
Методы программной генерации случайных чисел рассмотрены в теме 8.
Практика показывает, что результаты имитационного моделирования существенно зависят от качества используемых последовательностей псевдослучайных чисел. Поэтому применяемые в ИМ генераторы СЧ должны пройти тесты на пригодность.
Основные анализируемые характеристики генерируемых датчиком последовательностей:
- равномерность;
- стохастичность (случайность);
- независимость.
Рассмотрим методы проведения такого анализа, наиболее часто применяемые на практике.
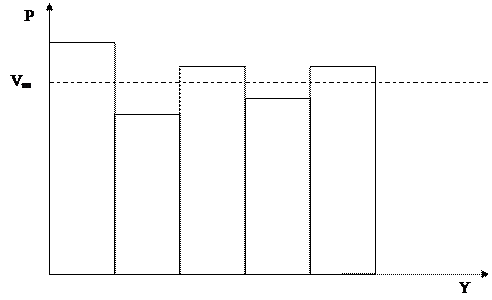 |
Рис. 9.1. Частотная гистограмма последовательности СЧ
Проверка равномерности может быть выполнена с помощью гистограммы относительных частот генерируемой СВ. Для ее построения интервал [0; 1] разбивается на т равных частей и подсчитывается относительное число попаданий значений СВ в каждый интервал. Чем ближе огибающая гистограммы к прямой, тем в большей степени генерируемая последовательность отвечает требованию равномерности распределения (рис. 9.1).
Проверка стохастичности. Рассмотрим один из основных методов проверки - метод комбинаций. Суть его сводится к следующему. Выбирают достаточно большую последовательность случайных чисел хi и для нее определяют вероятность появления в каждом из хi. ровно j единиц. При этом могут анализироваться как все разряды числа, так и только l старших. Теоретически закон появления j единиц в l разрядах двоичного числа может быть описан как биномиальный закон распределения (исходя из независимости отдельных разрядов).
Проверка независимости проводится на основе вычисления корреляционного момента.
Напомним, что две случайные величины а и b называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. Для независимых СВ корреляционный момент равен нулю.
Моделирование случайных событий. Для моделирования случайного события A, вероятность которого равна Рс, достаточно сформировать одно число r, равномерно распределенное на интервале [0, 1].
При попадании r в отрезок [0, Рс] считают, что событие A наступило, в противном случае - не наступило, т. е.: A=1, если r принадлежит отрезку [0, Pc ], и A=1- иначе.
Для моделирования полной группы N несовместных событий A={A1, A2,..., AN} с вероятностями соответственно P1, P2,..., PN также достаточно одного значения r, значение которого определяет промежуток случайного события.
Моделирование дискретных случайных величин. Наиболее часто используются два метода:
- метод последовательных сравнений;
- метод интерпретации.
Метод интерпретации основан на физической трактовке моделируемого закона распределения. Например, биномиальное распределение описывает число успехов в п независимых испытаниях с вероятностью успеха в каждом испытании Р и вероятностью неудачи g=1-P.
При моделировании этого распределения с помощью метода интерпретации выбирают п независимых СЧ, равномерно распределенных на интервале [0, 1], и подсчитывают количество тех из них, которые меньше Р. Это число и является моделируемой СВ.
Моделирование непрерывных СВ. При моделировании непрерывных СВ с заданным законом распределения могут используются три метода:
- метод нелинейных преобразований;
- метод композиций;
- табличный метод.
Первые два метода требуют от разработчика модели весьма серьезной математической подготовки. Третий метод, условно названный «табличным», основан на замене закона распределения непрерывной СВ специальным расчетным соотношением, которое позволяет вычислять значение СВ по значению случайного числа, равномерно распределенного все на том же промежутке [0, 1]. Такие соотношения получены практически для всех наиболее распространенных видов распределений и приведены в справочной литературе. В качестве примера ниже даны расчетные соотношения для двух законов распределения:
1. показательного:
 ,
,
где λ — параметр показательного распределения,
r— равномерно распределенное СЧ.
2. нормального:
 ,
,
т, s — параметры нормального закона распределения,
ri — равномерно распределенное СЧ.
В одной и той же имитационной модели могут фигурировать различные случайные факторы, одни могут быть представлены как случайные события, другие — как случайные величины; более того, если моделируется поведение достаточно сложной системы, то ее функционирование может быть связано с возникновением нескольких типов событий и учетом большого числа случайных величин, распределенных по различным законам. Если же моделирование всех случайных факторов основано на использовании одного датчика, генерирующего одну «общую» последовательность случайных чисел, то с математической точки зрения их нельзя считать независимыми. В связи с этим для моделирования каждого случайного фактора стараются использовать отдельный генератор, или, по крайней мере, обеспечивать создание новой последовательности случайных чисел. Во многих специализированных языках и пакетах моделирования такая возможность предусмотрена.
Контрольные вопросы
1. Перечислите показатели случайных чисел, сгенерированных на компьютере.
2. Как происходит моделирование случайных событий?
3. Какие используют методы для моделирования непрерывных случайных величин?
4. Выведите формулу для моделирования показательного закона распределения.
5. Какие необходимы параметры для моделирования нормального закона распределения?