Матрицы и СЛАУ

Основные понятия

Понятие множества. Отношения между множествами. Операции над множествами. Понятие n-арной алгебраической операции. Типы алгебраических операций. Нульарная и унарная операции. Понятие бинарного отношения. Отношение эквивалентности. Отношение порядка. Множества с одной алгебраической операцией, понятие группы. Множества с двумя алгебраическими операциями, понятие кольца и поля. Векторные пространства и алгебры. Подсистемы алгебраических систем, изоморфизм. Понятие оператор. Понятие базис

Комплексные числа

Понятие комплексного числа. Алгебраическая, тригонометрическая и показательная формы комплексного числа. Модуль комплексного числа. Аргумент комплексного числа. Формула Эйлера. Формулы Муавра. Свойства комплексных чисел. Приведение выражений, содержащих в знаменателе единицы мнимоедности к алгебраической форме комплексного числа.

Векторная алгебра

Основные понятия векторов. Линейные операции над векторами. Проекция вектора на ось. Разложение вектора по ортам координатных осей. Норма вектора. Ортонормированный вектор. Направляющие косинусы. Действия над векторами, заданными проекциями. Понятие скалярного произведения векторов и его свойства. Выражение скалярного произведения через координаты. Приложение скалярного приложения. Понятие векторного произведения и его свойства. Выражение векторного произведения через координаты. Приложение векторного приложения. Понятие смешанного произведения векторов и его свойства. Выражение смешанного произведения через координаты.

Матрицы и СЛАУ

Сложение матриц и умножение матрицы на число. Умножение матриц. Определители и их свойства. Непосредственное вычисление определителей второго и третьего порядка. Матричная запись систем линейных алгебраических уравнений. Ранг матрицы. Дефект матрицы. Невырожденные и вырожденные квадратные матрицы. Совместность или не совместность СЛАУ. Понятие обратной матрицы. Нахождение обратной матрицы с помощью элементарных преобразований.Нахождение решения неоднородных СЛАУ, имеющих единственное решение: а) методом Крамера, б) методом Гаусса, в) матричным методом. Фундаментальная система решений однородной системы. Ядро фундаментальной системы. Общее решение для неоднородных СЛАУ (имеющих множество решений). Собственные значения и собственные векторы оператора. Разложение вектора по векторам , , 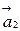в каноническом базисе пространства . Перевод оператора матрицы в новое каноническое пространство .