
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эвольвента окружности, ее уравнения и свойства.
|
|
Эвольвентой называется кривая, очерчиваемая точкой прямой, при перекатывании этой прямой по окружности без проскальзывания (рис. 1). В теории зацепления прямую называют производящей (образующей), а окружность – основной окружностью (радиус rb).
 Рассмотрим построение эвольвенты Е (рис. 1). В произвольной точке эвольвенты М проведем нормаль, которая касается основной окружности в точке В, получаем радиус кривизны эвольвентыρ.
Рассмотрим построение эвольвенты Е (рис. 1). В произвольной точке эвольвенты М проведем нормаль, которая касается основной окружности в точке В, получаем радиус кривизны эвольвентыρ.
Из прямоугольного треугольника Δ ОВМ найдем катет МВ:

 Из условия образования эвольвенты радиус кривизны МВ должен быть равен длине развертываемой дуги АВ основной окружности: È АВ = rb × (q + a),
Из условия образования эвольвенты радиус кривизны МВ должен быть равен длине развертываемой дуги АВ основной окружности: È АВ = rb × (q + a),
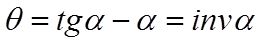 где q-полярный угол наклона радиус вектора; a -угол между направлением радиус вектора и направлением радиуса основной окружности проведенного в точке касания нормали. Отсюда:
где q-полярный угол наклона радиус вектора; a -угол между направлением радиус вектора и направлением радиуса основной окружности проведенного в точке касания нормали. Отсюда:
Разность тангенса и угла представляет собой эвольвентную функцию называемую инволютой. Инволюта является параметром для геометрических расчетов зубчатых механизмов.
Свойства эвольвенты:
· эвольвента не имеет точек внутри основной окружности;
· нормаль к любой точке эвольвенты направлена по касательной к основной окружности;
· центр кривизны эвольвенты лежит в точке касания нормали с основной окружностью.