
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет формулы дифракционной решетки
|
|
Рассмотрим дифракцию монохроматического света с длиной волны l, падающего на поверхность решетки (рис. 1). Лучи I и II усиливают друг друга, если они приходят на экран в одинаковых фазах; значит условия образования максимумов (светлых полос) заключается в том, что разность хода лучей D равна целому кратному длины волны:

| (1) |
где

| – условие образования главных максимумов |

| – постоянная решетки, |
| j | – угол, который образуют лучи с нормалью решетки. |
Из условия (1) следует, что при n = 0

|
на экране получается максимум, называемый нулевым.
При
 , ,
|
по обе стороны от нулевого возникает два дифракционных максимума I порядка,
а при
 , ,
|
соответственно два максимума II порядка.
Интенсивность максимумов постепенно убывает, а число их ограничено условием:
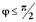 , ,
|
или согласно (1)

|
Решая уравнение (1) относительно l, получим:
 . .
| (2) |
Это выражение является основной расчетной формулой для вычисления световых волн при помощи дифракционной решетки и называется формулой дифракционной решетки.
Из формулы (2) следует, что для различных длин волн положение световых максимумов разное, если освещать дифракционную решетку белым светом, то на экране вместо светлых полос будут видны цветные полосы (спектры), которые соответственно называют спектром первого порядка и т. д. В каждой полосе красная линия спектра согласно (2) отклонена больше, чем фиолетовая линия.
Линии спектров высоких порядков менее интенсивны и практически ясно наблюдаются лишь в спектрах не выше третьего порядка