
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
На минимум 4 страница
|
|
1097.Решение несбалансированной транспортной задачи линейного программирования с дополнительными условиями.
1. Запрет поставки: необходимо в связи установить max расстояние (например, 100) и решить ТЗЛП.
2. Израсходовать запас поставщика в полном объеме [отдать реальным потребителям]:
необходимо запретить поставку дополнительному потребителю, т.е. в дополнительной связи установить max расстояние (например, 100) и решить ТЗЛП.
Удовлетворить потребность потребителя в полном объеме [получит от реальных постав щиков]: необходимо запретить доставку от дополнительного поставщика, т.е. в дополни- тельной связи установить max расстояние (например, 100) и решить ТЗЛП.
3. Организовать недоввоз потребителю: необходимо создать поставку от дополнительно- го поставщика, установив в дополнительной связи min расстояние (например, 1) и решить ТЗЛП.
Организовать недовывоз от поставщика: необходимо создать запас у дополнительного потребителя, т.е. установить в дополнительной связи min расстояние (например, 1) и решить ТЗЛП.
2) корректируются объемы поставщика и потребителя (отнимаем у поставщика и у пот- ребителя заданный объем).
3) решается ТЗЛП.
5. Гарантия (обеспечить) поставки в связь НЕ БОЛЬШЕ: 1) решается задача без ограниче- ния;
3) корректируются объемы поставщика и потребителя (отнимаем у поставщика и у пот- ребителя заданный объем);
4) организовать запрет поставки в заданную связь, установив в ней max расстояние (на- пример, 100);
5) решить ТЗЛП.
11008.Решение транспортной задачи линейного программирования с ограничением на размер корреспонденции
При наличии ограничений на размер корреспонденций, задача в дальнейшем решается по следующей схеме:
1) проверяется выполнение условия Xij £ Xoij для связей ij. Если условие выполняется для всех связей, то решение закончено (переход на блок 10 общего алгоритма), иначе переход на пункт 2;
2) для каждой связи ij, по которой имеет место условие Xij > Xoij , последовательно должен быть реализован алгоритм:
2.3) в окончательное решение вводится корреспонденция Xij = Xoij ;
2.4) корректируются соответствующие размеры наличия и потребности в ресурсе
XА j =XА j - Xij ;
XBj = XBj - Xij ;
2.3) корректируется соответствующая стоимость (расстояние) поставки lij путем замены на большое число, например  ;
;
3) переход на блок 4 укрупненного алгоритма решения задачи
11109.Схема решения транспортной задачи линейного программирования без дополнительных условий.
Ввод исходных данных: число и
название пунктов, объемы запасов
и потребностей ресурса, стоимос-
ти возможных поставок на едини-
цу ресурса, ограничения на
размер корреспонденций 3
Да Введение фиктивного поставщика 2 (потребителя), объема ресурса по
Нет нему, условных стоимостей пос-
Наличие баланса? тавок и ограничений
Да
4
Составление первоначального ба-
зисного плана поставок ресурса
(с учетом стоимостей)
Да
План оптимален?
Нет
Улучшение плана поcтавок
путем их перераспределения
7
Вывод результата решения:
название корреспондирующих
пунктов, размер и стоимость
поставок ресурса
111.112.114.
Задача упорядочения – это задача определения оптимальной последовательности событий, а задачи согласования охватывают сетевое планирование и управление.
Основа решения первых – теория расписаний, вторых – теория графов.
Предметом сетевого планирования и управления (СПУ) является разработка и оптимизация сетевых графиков.
Сетевой график – это ориентированный граф, дуги которого имеют одну или несколько числовых характеристик. Дугами изображают работы, а вершинами – события.
Работа – это процесс, сопровождающийся затратами времени и ресурсов. Если имеются затраты только времени – это фиктивные работы (естественная сушка и т.п.).
Событие – это итог процесса или его части. Оно совершается, когда закончены все предшествующие ему работы.
Путь – это любая непрерывная последовательность работ от исходного события до завершающего (т.е. до конечной цели).
Длина пути определяется суммой продолжительности лежащих на нем работ.
Рассмотрим сетевой график с одним исходным и одним завершающим событием, известными продолжительностями tij работ ij, где i – событие, соответствующее началу работы и j – соответственно окончанию. Общее число событий m, число работ n.
Ниже приведен пример сетевого графика.
1 6
2 5
| i | J | tij |
Расчет сетевого графика включает отыскание следующих основных параметров:
ранний и поздний сроки начала работ tр.нij и tп.нij;
ранний и поздний сроки окончания работ tр.оij и tп.оij;
ранний и поздний сроки наступления событий Tрi и Tпi;
полный и свободный резервы времени каждой работы Rпij и Rсij;
резерв времени событий Ri;
критическое время графика tкр и перечень работ, образующих критический путь;
полный резерв Rl времени путей l, альтернативных критическому.
На основании этих характеристик определяется перечень работ, образующих критический путь – путь максимальной длины от начального до завершающего события, имеющий критическое время tкр.
Для расчета необходимо произвести правильную нумерацию событий, т.е. для любой работы ij номер предшествующего события i должен быть меньше номера последующего события j.
Алгоритм вычислений следующий:
1) Присваивается исходному событию начальный, например, нулевой момент времени раннего срока свершения Ti=1=0;
2) Последовательно для каждого j=2, 3,..., m рассчитываются
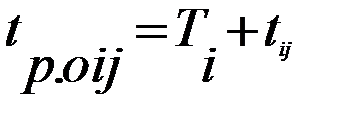 ;
;
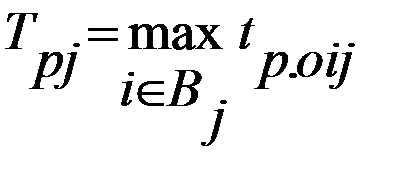
где Bj – множество событий i, соединенных работами с j- м событием.
В результате находятся Трi, i=1, m.
3) Критическое время сетевого графика tкр = Tрm .
4) Поздний срок свершения завершающего события принимается равным критическому tкр или заданному директивному времени tдир (tдир ³ tкр ):
Tпm = tкр или Tпm = tдир.
5) Последовательно для каждого пункта i = m-1, m-2,..., 1 рассчитываются
 ;
;
 ,
,
где Ai – множество событий j, соединенных работами с i-м событием.
6) Рассчитываются резервы времени событий
Ri = Tпj - Tрi.
7) Рассчитываются полные резервы времени работ – максимальное время на которое можно отсрочить или увеличить продолжительность работы ij, не изменяя установленного позднего срока наступления завершающего события
Rпij = Tпj - tр.оij= Tпj - Tрi - tjj.
8) Рассчитываются свободные резервы времени работ – максимальное время на которое можно отсрочить или увеличить продолжительность работы ij, при условии, что все события будут выполнены в свои ранние сроки
Rсij = Tрj - tр.оij = Tрj - Tрi – tij.
Величина свободного резерва меньше или равна величине полного резерва.
9) Определяется критический путь. Это путь, продолжительность которого равна критическому времени – минимальному времени, в течение которого может быть выполнен весь процесс и проходит через события с нулевым резервом времени и включает работы с нулевым полным резервом.
10) Полный резерв времени интересующих альтернативных путей определяется как разность между длиной критического пути и длиной любого другого полного пути tl
Rl = tкр - tl.
113.
Для получения начального базисного решения рассмотрим применение метода минимального элемента. В соответствии с этим методом распределение составляется по следующему алгоритму:
1) формируются дополнительные массивы стоимостей (расстояний) l'ij (l'ij = l ij), объемов ресурса X'Ai (X'Ai=XAi) и X'Bj (X'Bj =XBj), i=1, 2,..., m; j=1.2,..., n;
2) находится минимальное расстояние (стоимость) из всех связей
 .
.
Если lrw = ¥, то первоначальное базисное решение получено. Иначе на п.3;
3) связь rw, соответствующая минимальному расстоянию (стоимости), загружают корреспонденцией Xrw. Объем корреспонденции Xrw , назначаемый для связи rw, определяется как минимум от объемов запаса и потребности с учетом ранее назначенных других поставок:
Xrw = min (X'Ar, X'Bw),
где X'Ar – количество ресурса r-го поставщика с учетом ранее назначенных корреспонденций другим, кроме w-го, потребителям; X'Bw – количество ресурса, требуемого w-му потребителю с учетом ранее назначенных корреспонденций от других, кроме r-го поставщика;
4) из сравниваемых величин X'Ar и X'Bw вычитается значение Xrw , в результате чего получаются измененные ограничения X'Ar =X'Ar - Xrw и X'Bw =X'Bw - Xrw ;
5) изменяется массив l'ij по следующему правилу:
l'iw = ¥ (i= 1, 2,..., m), если X'Bw=0
иначе если X'Ar=0, то l'rj = ¥ (j= 1, 2,..., n);
6) переход на пункт 2).
Пункт 5 алгоритма обеспечивает исключение из дальнейшего рассмотрения поставщика (если X'Ar =0), либо получателя (если X'Bw=0). Остаток объема ресурса X'Ar или X'Bw к дальнейшему распределению может иметь значение, равное нулю.
Полученное таким образом закрепление потребителей ресурса за поставщиками является одним из возможных базисных распределений.
Для оценки оптимальности текущего решения закрепления потребителей ресурса за поставщиками применяется ряд методов: распределительные методы (метод Хичкока, метод Креко, метод МОДИ), методы с разрешающими элементами (метод разрешающих слагаемых и метод разрешающих множителей) и др.
Наиболее широкое применение получил модифицированный метод (МОДИ). В распределительную таблицу вводят вспомогательные строку и столбец; в них вносят специальные показатели, называемые потенциалами. Распределительные методы основаны на следующем: если к расстояниям любой строки (столбца) распределительной таблицы прибавить (или отнять) одно и то же произвольное число, то оценка оптимальности относительно не изменится. Если, например, от расстояний каждого i-го отправителя отнять число uAi , а от расстояний каждого j-го потребителя – uBj, то относительной оценкой любой связи ij может служить параметр sij (вместо l ij):
sij = lij - uAi- uBj. (3.6)
Принимая для загруженных связей sij = 0 и используя выражение (3.6), определяются потенциалы uAi и uBj по следующему правилу:
потенциал для одного пункта, например первого поставщика принимается равным нулю;
по расстояниям загруженных связей подбираются потенциалы для других поставщиков и потребителей таким образом, чтобы соблюдалось принятое условие lij - uAi- uBj = 0, т.е. расстояние для каждой загруженной связи должно быть равно сумме потенциалов по ее поставщику и потребителю.
Затем по вычисленным потенциалам uAi , uBj определяется, используя формулу (3.6), значение оценочного параметра sij для каждой незагруженной связи (не входящей в базисный план). Величина параметра sij характеризует общее изменение целевой функции, получаемое при включении в план единичной корреспонденции для связи ij по сравнению с рассматриваемым планом.
Если значение оценочного параметра свободной связи будет меньше нуля (sij < 0), то это значит, что перераспределение корреспонденций с загрузкой такой связи, называемой потенциальной, уменьшит значение целевой функции на величину abs(sijXij), Xij – размер корреспонденции, которой будет загружена связь ij. Отсутствие связей со значением параметра sij < 0 означает, что проверяемый план закрепления потребителей за поставщиками является оптимальным. Если для какой-то свободной связи значение sij равно нулю, то это означает, что можно получить другой план с тем же минимальным значением целевой функции.
Если решение не оптимально, то из всего множества свободных связей выявляется наиболее потенциальная с минимальным значением sij. Загрузка корреспонденцией такой связи дает наибольшее уменьшение целевой функции на каждую единицу перераспределенного объема ресурса.
При перераспределении загрузок по связям в распределительной таблице для наиболее потенциальной связи, как для загруженной, строится контур. Введение к m+n-1 загруженным связям еще одной образует ровно один определенный контур, присущий вводимой связи. После чего связи, соответствующие вершинам контура, нумеруются: номер 1 присваивается выбранной потенциальной связи, а дальнейшая нумерация ведется в порядке следования вершин по контуру (могут присваиваться связям контура положительные и отрицательные знаки).
Затем производится перераспределение по контуру корреспонденций следующим образом:
1) выявляется связь с четным номером, которой соответствует наименьшее значение корреспонденции Xм ;
3) значение объема ресурса Xм вычитается от значений объемов корреспонденций всех связей с четными номерами вершин. Если среди связей с четными номерами вершин окажутся две (или более) с одинаковой минимальной корреспонденцией, то из плана исключается только одна из них, для связи с большим расстоянием поставки, а вместо остальных оставляют условную корреспонденцию с нулевым значением, чтобы не допустить вырождения;
3) для всех связей с нечетными номерами вершин (включая и потенциальную) к значениям объемов корреспонденций прибавляется величина Xм.
В результате одна связь становится свободной, а наиболее потенциальная – получает загрузку. Измененные значения корреспонденций и значения объемов корреспонденций для связей, которые не входили в контур, переносятся в таблицу нового улучшенного плана закрепления потребителей за поставщиками.
Полученный новый план проверяется на оптимальность. Действия по проверке на оптимальность и улучшению распределения повторяются до тех пор, пока не будет найден оптимальный план закрепления поставщиков за потребителями.
При решении транспортной задачи линейного программирования на основе существующего базисного решения возможны варианты, когда число загруженных связей в таблице меньше m+n-1 (случай вырождения) или больше m+n-1 (случай наличия циклов). В первом случае нельзя оценить оптимальность решения, так как невозможно определить потенциалы для некоторых поставщиков и (или) потребителей, во втором – потенциалы определяются неоднозначно.
В случае вырождения необходимое число свободных связей загружают нулями с соблюдением правила: нулевые объемы поставок заносятся для связи поставщиков (потребителей), для которых нельзя рассчитать потенциал, с поставщиками (потребителями), для которых потенциалы уже определены. Целесообразно выбрать из данных связей такие, которым соответствуют наименьшие расстояния поставок. Связи, загруженные нулями, не должны образовывать контуров (циклов) с другими загруженными связями.
В случае наличия циклов для некоторых связей исключают корреспонденции по следующему алгоритму:
1) строится один из возможных контуров;
2)нумеруются углы контура;
3) определяется сумма стоимостей (расстояний) поставок для связей, в которых лежат углы контура с четными номерами и затем с нечетными номерами;
4) среди связей (с четными или нечетными номерами), для которых сумма стоимостей перевозок больше, выявляется связь с наименьшим значением размера корреспонденции Xм;
5) размер корреспонденции Xм вычитается от загрузки каждой из связей с четными или нечетными номерами, для которых сумма расстояний поставок больше, и прибавляется к загрузке каждой из связей с нечетными или четными номерами, для которых сумма расстояний поставок меньше.
Указанные действия повторяются до полного исключения циклов (контуров) в распределительной таблице. При этом нельзя допускать вырождения за счет одновременного исключения загрузок для нескольких связей одного цикла. Исключение контуров в распределительной таблице по вышеописанной методике уменьшает одновременно и значение целевой функции.
При отсутствии дополнительных условий полученное оптимальное решение является окончательным.
117.