
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос 10
|
|
Энергетические соотношения в цепях постоянного тока
Важное значение при исследовании электротехнических устройств имеет анализ энергетических соотношений. Электрическая мощность характеризует скорость передачи или преобразования электрической энергии. Единица мощности [Вт] –(Ватт). По закону сохранения энергии для замкнутой цепи вся мощность, которая вырабатывается источниками энергии, должна полностью поглощаться потребителями энергии.
Равенство мощностей генераторов (источников) и приемников (нагрузок) называют балансом мощностей:
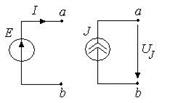
 .
.
Расчет мощности источников проводится следующим образом:
Если условно-положительные направления токов и напряжений на источниках выбраны соответственно рисунку, то  ,
, 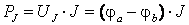 .
.
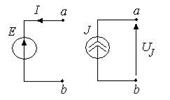 Расчет мощности источников проводится следующим образом:
Расчет мощности источников проводится следующим образом:
Если условно-положительные направления токов и напряжений на источниках выбраны соответственно рисунку, то  ,
,

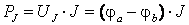 .
.
При таком выборе направлений
 ,
,
 . Мощность приемника (резистора) по формуле Джоуля-Ленца равна
. Мощность приемника (резистора) по формуле Джоуля-Ленца равна
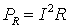 .
.
Таким образом, должно выполняться равенство
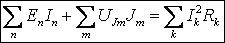 .
.
Вопрос 11
Области применения электротехнических устройств переменного тока
Переменный электрический ток- электрический ток, который через равные промежутки времени изменяется по величине и направлению. Почти вся электрическая энергия вырабатывается в виде переменного электрического тока. Именно поэтому его значение велико и область его применения широка.
Генератор переменного тока. В 1832-м году неизвестным изобретателем был создан первый однофазный синхронный многополюсный генератор переменного тока. Но в самых первых электронных устройствах применялся только постоянный ток, в то время как переменный ток долгое время не мог найти своего практического применения. Тем не менее, вскоре выяснили, что намного практичнее использовать не постоянный, а переменный ток, то есть тот ток, который периодически меняет свое значение и направление. Преимущества переменного тока, состоят в том, что его удобнее вырабатывать при помощи электростанций, генераторы переменного тока экономичнее и проще в обслуживании, чем аналоги, работающие на постоянном токе. Поэтому были собраны надежные электрические двигатели переменного тока, которые сразу нашли свое широкое применение в промышленных и бытовых сферах. Надо отметить, что благодаря существованию переменного тока, его особенным физическим явлениям, смогли появиться такие изобретения, как радио, магнитофон и прочая автоматика и электротехника, без которой сложно представить современную жизнь.
4 Существуют промышленные и бытовые генераторы: Промышленные генераторы- наилучший вариант для использования на производстве, в больницах, школах, магазинах, офисах, бизнес центрах, а так же на строительных площадках, значительно упрощая строительство в тех зонах, где электрификация полностью отсутствует. Бытовые генераторы, более практичные, компактные и идеально подходят для использования в коттедже и загородном доме. Генераторы переменного тока широко применяются в различных областях и сферах благодаря тому, что могут решить множество важных проблем, которые связаны с нестабильной работой электричества или полным его отсутствием.
5 Применение в сельском хозяйстве. В с/х используются дизельные генераторы, которые обеспечивают сельскохозяйственную технику (насосы, оборудования, освещение), продление светового дня (для теплиц и птичников), отопление, доильные аппараты и т.д. Также в борьбе с вредителями сельскохозяйственных культур используется низкочастотное излучение квантового генератора в который записана информация снятая с оригиналов применяемых для локализации различных болезней и удаления насекомых.
ВОПРОС 12
Представление синусоидальных величин комплексными числами.
Вращающиеся векторы синусоидальных величин можно изобразить на комплексной плоскости. При этом ось абсцисс совпадает с осью действительных чисел (ось +1), а ось ординат с осью мнимых величин (+j). Любому вектору на комплексной плоскости соответствует определенное комплексное число (рисунок 3.3). Так вращающемуся вектору, синусоидальной величины  , будет соответствовать комплексное число:
, будет соответствовать комплексное число:


Рисунок 3.3 - Комплексное представление синусоидальной величины
Комплексное число, соответствующее положению вектора в начальный момент времени (t = 0) 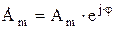 - называют комплексной амплитудой синусоидальной величины. При увеличении во времени фазы синусоидальной величины угол между вектором и осью растет, функцию поворота вектора на угол
- называют комплексной амплитудой синусоидальной величины. При увеличении во времени фазы синусоидальной величины угол между вектором и осью растет, функцию поворота вектора на угол  относительно начального положения выполняет комплексное число
относительно начального положения выполняет комплексное число 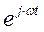 . Для анализа синусоидальных величин имеющих одинаковую частоту важно взаимное положение векторов в начальный момент времени, поэтому для расчета используют только комплексные амплитуды синусоидальных величин или комплексные действующие значения. Вектор на комплексной плоскости, длина которого равна действующему значению синусоидальной величины, и соответствующее этому вектору комплексное число называют комплексным действующим значением синусоидальной величины:
. Для анализа синусоидальных величин имеющих одинаковую частоту важно взаимное положение векторов в начальный момент времени, поэтому для расчета используют только комплексные амплитуды синусоидальных величин или комплексные действующие значения. Вектор на комплексной плоскости, длина которого равна действующему значению синусоидальной величины, и соответствующее этому вектору комплексное число называют комплексным действующим значением синусоидальной величины:
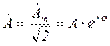
Представление синусоидальной величины комплексной амплитудой или действующим значением аналогично представлению с помощью вращающегося вектора. Однако представление синусоидальных величин в комплексной форме позволяет применить эффективный комплексный метод расчета цепей синусоидального тока, то есть сложение и вычитание векторов заменить сложением и вычитанием комплексных чисел.
Применяются три формы записи комплексного значения синусоидальной величины:
 - показательная форма,
- показательная форма,
 - тригонометрическая форма,
- тригонометрическая форма,
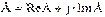 - алгебраическая форма,
- алгебраическая форма,
где 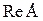 и
и  - действительная и мнимая часть комплексного значения синусоидальной величины. Переход от алгебраической формы к показательной осуществляется по формулам:
- действительная и мнимая часть комплексного значения синусоидальной величины. Переход от алгебраической формы к показательной осуществляется по формулам:
 ,
,
 .
.
Переход от показательной формы к тригонометрической осуществляется по формуле Эйлера:
 .
.
Сложение и вычитание комплексных величин производится в алгебраической форме, а умножение и деление в показательной. При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных величин, сокращенно их называют комплексными значениями.
ВОПРОС 13
Пассивные и активные двухполюсники.
Двухполюсником называется часть электрической цепи любой сложности и произвольной конфигурации, выделенная относительно двух зажимов (двух полюсов).
Двухполюсник, не содержащий источников энергии или содержащий скомпенсированные источники (суммарное действие которых равно нулю), называется пассивным. Если в схеме двухполюсника имеются нескомпенсированные источники, он называется активным. На схеме двухполюсник обозначают прямоугольником с двумя выводами (рис. 1.14). Это обозначение можно условно рассматривать как коробку, внутри которой находится электрическая цепь.

Пассивный двухполюсник является потребителем энергии и может быть заменен эквивалентным сопротивлением, величина которого равна входному сопротивлению двухполюсника (см., например, рис. 1.15).

ВОПРОС 14
ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В ЦЕПЯХ переменного тока
Мощность в цепи синусоидального тока. Активная мощность. При изменении тока и напряжения в течение периода мощность p = ui, потребляемая двухполюсником при токе i = Im sin (w t + y i) и напряжении на зажимах u = Um sin (w t + y u) также будет переменной в течение периода.
Мгновенная мощность

имеет постоянную составляющую — среднюю за период активную мощность  и переменную синусоидальную составляющую
и переменную синусоидальную составляющую  .
.
Активная мощность, потребляемая двухполюсником при синусоидальном токе, зависит не только от напряжения и тока, но и от угла фазового сдвига j между ними. Для индуктивного и емкостного элементов при j = ± p/2 активная мощность равна нулю, так как эти элементы в течение отдельных частей периода лишь накапливают энергию и затем отдают ее другим элементам.
Из него следует, что мгновенная мощность изменяется по синусоидальному закону с частотой, равной удвоенной частоте тока и напряжения. В общем случае (при произвольном значении j) имеются промежутки времени, в течение которых мощность отрицательна; при этом запасенная энергия отдается другим участкам цепи. Средняя же за период мощность P положительна, так как для пассивного двухполюсника угол фазового сдвига лежит в пределах – p/2 £ j £ p/2 и, следовательно, коэффициент мощности cos j ³ 0.
Формулу для активной мощности при синусоидальном токе можно также записать в виде
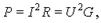
где R и G – эквивалентные входное сопротивление и проводимость двухполюсника.
Условия выделения максимальной мощности в приемнике. Определим активную мощность в нагрузке простейшей цепи синусоидального тока, питаемой от источника ЭДС с действующим значением E 0 и внутренним активным и реактивным сопротивлениями R 0 и X 0 (рис. 7.8).
 Pис. 7.8
Pис. 7.8
| Параметры нагрузки необходимо подобрать так, чтобы выделяемая в ней активная мощность P н имела максимальное значение. Так как действующее значение тока в цепи равно
 то для активной мощности P н будем иметь
то для активной мощности P н будем иметь

|
Анализ этого выражения на максимум приводит сразу к требованию X н = – X 0. Если это условие считать выполненным, то для активной мощности получим более простое соотношение 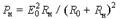 , справедливое, очевидно и для цепи постоянного тока, включающей только резистивные элементы. Анализ последней формулы на максимум дает
, справедливое, очевидно и для цепи постоянного тока, включающей только резистивные элементы. Анализ последней формулы на максимум дает

откуда легко найти, что R 0 = R н.
Таким образом, условия согласования нагрузки и источника, обеспечивающие максимальную мощность в приемнике, имеют вид:

При выполнении этих условий в нагрузке выделяется мощность, равная  . Однако подобный режим работы характеризуется низким коэффициентом полезного действия. Так как при выполнении условий согласования мощности в сопротивлениях R 0 и R н одинаковы и КПД, определяемый как отношение мощности, потребляемой в нагрузке, к мощности, вырабатываемой источником, составляет лишь 50%. Поэтому режим согласования не применяют в системах, связанных с передачей значительных мощностей, однако в маломощных электронных устройствах его применение целесообразно.
. Однако подобный режим работы характеризуется низким коэффициентом полезного действия. Так как при выполнении условий согласования мощности в сопротивлениях R 0 и R н одинаковы и КПД, определяемый как отношение мощности, потребляемой в нагрузке, к мощности, вырабатываемой источником, составляет лишь 50%. Поэтому режим согласования не применяют в системах, связанных с передачей значительных мощностей, однако в маломощных электронных устройствах его применение целесообразно.
Вопрос 15
Анализ состояния электрических цепей
| E1, В | Е2, В | R1ьОм | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | r01, Ом | r02, Ом | |
Таблица 1.1 - Числовые параметры электрической цепи постоянного тока
1) Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях
Метод узловых и контурных уравнений основан на применений первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи.
При расчете данным методом произвольно задали направления токов в ветвях I1, I2, I3, I4, I5
Составим систему уравнений. В системе должно быть столько уравнений, сколько в цепи ветвей (неизвестных токов)
В заданной цепи шесть ветвей, значит, в системе должно быть шесть уравнений (m=6). Сначала составляем уравнения для узлов по первому закону Кирхгофа.
Для цепи с n-узлами можно составить (n=1) независимых уравнений. В нашей цепи при узлах (A, B, C), значит, число уравнений: n-1=4-1=3
Составляем два уравнения для любых 2-х узлов, например для узлов А, В и С
Всего в системе должно быть шесть уравнений. Три уже есть. Три недостающих уравнения составляю по второму закону Кирхгофа, выбрав для этого определенные контуры. Принимаю обход контура по часовой стрелки и, учитывая правила знаков, получаю три недостающих уравнения:
ЭДС в контуре берется со знаком " +”, если направление ЭДС совпадает с обходом контура, если не совпадает знак С.
Падение напряжения на сопротивлении контура берется со знаком " +”, если направление тока в нем совпадает с обходом контура, со знаком " -”, если не совпадает.
Мы получим систему из шести уравнений с шестью неизвестными: