
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 3
|
|
Провести термодинамический анализ форкамерного цикла ДВС, отнесенного к 1 кг воздуха с изохорно-изобарным подводом теплоты. Цикл (рисунок) состоит из четырех процессов:
политропного сжатия 1 – 2, изохорного 2 – 3 и изобарного 3 – 4 процессов подвода тепла, политропного расширения 4 – 5, изохорного 5 – 1 процесса отвода тепла.
Начальные параметры рабочего тела t1 (0 0C), Р1 (кПа) и характеристики цикла: степень сжатия ε, степень повышения давления λ и степень последующего расширения ρ принимать по исходным данным

Исходные данные:
t1 = 320C;
P1 = 80кПа;
n1 = 1, 32; n2 = 1, 20;
ε = 18; λ = 1, 3; ρ = 1, 6
Решение
Точка 1 – параметры начального состояния
а) Из уравнения Клайперона определяем начальный удельный объем:

где R – газовая постоянная воздуха, R = 0, 287 кДж/(кг К)
T1 = t1 + 273 = 32 + 273 = 305К;
Р1 = 80кПа = 80∙ 103 Па

б) Внутренняя энергия:

где cv – массовая изохорная теплоемкость воздуха, Дж/(кг∙ К)
cv = 0, 72 кДж/(кг∙ К)

б) Энтальпия:

где cp – массовая изобарная теплоемкость воздуха, Дж/(кг∙ К)
cp = 1, 01 кДж/(кг∙ К)

Точка 2 – конец политропного сжатия
а) Давление в конце процесса
Из уравнения политропы Р v n = const имеем:

где ν 1/ν 2 = ε – степень сжатие


б) Объем в конце процесса


в) Из уравнения Клайперона определяем температуру в конце сжатия:



г) Внутренняя энергия:


д) Энтальпия:


Точка 3 – конец изохорного подвода тепла
а) Объем по условию процесса
ν 3 = ν 2 = 0, 06м3/кг
б) Давление


в) Температура


г) Внутренняя энергия:


д) Энтальпия:


Точка 4 – конец изобарного подвода тепла
а) Давление по условию процесса
Р4 = Р3 = 4719кПа
б) Объем определяем из выражения степени предварительного расширения

в) Температура из уравнения



г) Внутренняя энергия:


д) Энтальпия:


Точка 5 – конец политропного расширения
а) Объем из условия изохорного процесса
ν 5 = ν 1 = 1, 09м3/кг
б) Давление из уравнения политропы

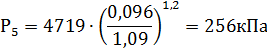
в) Температура из уравнения Клайперона



г) Внутренняя энергия:
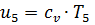

д) Энтальпия:


Параметры рабочего тела в цикле
| Точка | Р, кПа | ν, м3/кг | Т, К | u, кДж/кг | i, кДж/кг |
| 1, 09 | 219, 6 | ||||
| 0, 06 | 547, 2 | ||||
| 0, 06 | 711, 4 | ||||
| 0, 096 | |||||
| 1, 09 |
Процессы цикла
1. Процесс политропного сжатия 1 – 2 при n1
a) Изменение внутренней энергии:

б) Теплоемкость процесса:

где


в) Теплота, участвующая в процессе:

г) Работа сжатия:

д) Изменение энтальпии
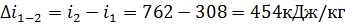
е) Изменение энтропии

2. Процесс 2 – 3 изохорного подвода тепла при теплоемкости сν = const
a) Изменение внутренней энергии:

б) Теплота процесса:

в) Работа процесса:

г) Изменение энтальпии

д) Изменение энтропии
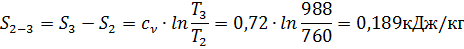
3. Процесс 3 – 4 изобарного подвода тепла при Р3 = соnst
a) Изменение внутренней энергии:

б) Теплота процесса:
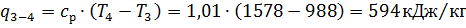
в) Работа процесса:
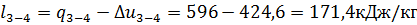
д) Изменение энтальпии

е) Изменение энтропии

4. Процесс политропного расширения 4 – 5 при n2
а) Изменение внутренней энергии:

б) Теплоемкость процесса:


в) Теплота, участвующая в процессе:

г) Работа сжатия:

д) Изменение энтальпии

е) Изменение энтропии

5. Процесс 5 – 1 изохорного отвода теплоты сν = const
а) Изменение внутренней энергии:

б) Теплота процесса:

в) Работа процесса:

г) Изменение энтальпии

д) Изменение энтропии

| Процесс | n | c, кДж/(кг∙ К) | Δ u, кДж/кг | q, кДж/кг | l, кДж/кг | Δ i, кДж/кг | Δ S, кДж/(кг∙ К) |
| 1 – 2 | 1, 32 | –0, 18 | 327, 6 | – 82 | –409, 6 | –0, 164 | |
| 2 – 3 | 164, 2 | 164, 2 | 0, 189 | ||||
| 3 – 4 | 424, 6 | 171, 4 | 0, 337 | ||||
| 4 – 5 | –436 | –610 | 0, 349 | ||||
| 5 – 1 | 1, 2 | –480, 4 | –480, 4 | –674 | –0, 835 |