Помехоустойчивое кодирование.

Задание:

1. Выписать первые буквы ФИО студента и записать их обычным двоичным пятиэлементным кодом в соответствии с прил.1.

2. Найти длину кода, если известно, что k=5 (пятиэлементная информационная комбинация), и код исправляет однократные ошибки.

3. Вывести кодирующие и проверочные уравнения для определенного в п.2 кода и закодировать кодом Хемминга первые буквы ФИО студента.

4. Показать, как определяют однократные ошибки в третьем и в седьмом разряде (первая буква отчества).

5. Построить структурную схему кодера выбранного кода Хемминга.

Решение:

Помехоустойчивое кодирование служит для повышения достоверности передачи дискретной информации в реальных системах связи при наличии помех, искажающих передаваемую информацию. Свойство коррекции (исправления) искаженной кодовой информации реализуется за счет создания избыточного кода, что позволяет разделить все кодовые комбинации на разрешенные (искаженные). При приеме неразрешенной ком­бинации можно сделать вывод о нарушении истинности передачи, а при определенных условиях и исправить это нарушение (отнести значение неразрешенной комбинации к ближайшему значению разрешенной комбинации). Свойства обнаружения и исправления ошибок определяются дополнительными (проверочными) элементами (разрядами) кода, количество которых определяет возможности кода. Так, например, 1 или 2 дополни­тельных элемента позволяют обнаружить однократные (в одном разряде), при трех дополнительных (проверочных) элементах можно исправить однократные ошибки (в одном разряде). Любой блочный корректирующий код содержит n элементов, из которых k-информационных и r-проверочных (дополнительных) элементов. Тогда код обозначают: код (n, k), n=k + r.

Код Хемминга относится к блочным (каждый передаваемый символ передается двоичным кодом, где каждая разрешенная комбинация имеет длину — n элементов), разделимым (в каждом блоке можно отдельно выделить информационные элементы и проверочные), систематическим (все передаваемые символы представляются одинаковым по размеру — n-блочным кодом). В теории кодирования действует арифметическое пространство, действия в котором определяются суммированием по модулю 2 (четностью), обозначается ⊕ (1⊕ 1= 0; 1⊕ 0 = 1).

1. Выпишем первые буквы ФИО:

Ш Е А

Запишем их обычным двоичным пятиэлементным кодом:

Ш – 11001

Е – 00110

А – 00001.

2. Длину кодовой комбинации n-кода Хемминга, исправляющего однократные ошибки при заданном числе информационных элементов k, можно определить из неравенства:

k=5

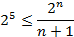
При n=9 условие выполняется .

Число проверочных элементов r=4.

3. Составим матрицу возможных однократных (в одном разряде) ошибок и «синдромов» ошибки (указатель разряда, в котором случилось ошибка).

Выберем места (разряды) для проверочных элементов, для чего выделяем те синдромы, где единица встречается один раз (первый второй и четвертый разряды). В остальных разрядах разместим передаваемую информацию:

Для Ш: .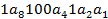

Для Е: .

Для А: .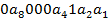

Здесь - проверочные элементы, которые найдем из данных информационных элементов по правилу, определяемому по столбцу синдрома:

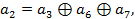
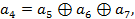
Для Ш:

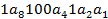
Теперь запись закодированного блока: 111001101, где по-прежнему 1, 2, 4, 8 – разряды проверочные.

Для Е:

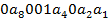
Теперь запись закодированного блока: 000110011, где по-прежнему 1, 2, 4, 8 – разряды проверочные.

Для А:

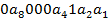
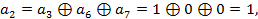
Теперь запись закодированного блока: 000000111, где по-прежнему 1, 2, 4, 8 – разряды проверочные.

Закодировали кодом Хемминга первые буквы ФИО студента:

Ш Е А – 111001101 000110011 000000111

На приемной стороне проводится проверка принятой комбинации и в случае однократной ошибки определяется «синдром» ошибки, указывающий место (разряд), где произошла ошибка. Исправление ошибки осуществляется простым инвертированием значения указанного разряда.

Проверочные уравнения:

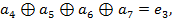
Синдром ошибки - указывает место (разряд), где произошла ошибка.

4. Покажем, как определяют однократные ошибки в третьем и в седьмом разряде (первая буква отчества).

Первая буква отчества – А: 000000111.

Допустим, однократная ошибка произошла в третьем разряде, т.е. передавалась комбинация 000000111, а принята 000000011. Проверочные уравнения приводят к результату:

Синдром ошибки – 0011 указывает на ошибку в третьем разряде, исправим 0→ 1 и получаем исправленную комбинацию в виде 000000111, что и передавалось.

Допустим, однократная ошибка произошла в седьмом разряде, т.е. передавалась комбинация 000000111, а принята 001000111. Проверочные уравнения приводят к результату:

Синдром ошибки – 0111 указывает на ошибку в седьмом разряде, исправим 1→ 0 и получаем исправленную комбинацию в виде 000000111, что и передавалось.