
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определения. Допустим, у нас есть бесконечно малые при одном и том же величины и (либо, что не важно для определения
|
|
Допустим, у нас есть бесконечно малые при одном и том же  величины
величины 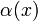 и
и  (либо, что не важно для определения, бесконечно малые последовательности).
(либо, что не важно для определения, бесконечно малые последовательности).
§ Если  , то
, то  — бесконечно малая высшего порядка малости, чем
— бесконечно малая высшего порядка малости, чем 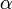 . Обозначают
. Обозначают  .
.
§ Если  , то
, то  — бесконечно малая низшего порядка малости, чем
— бесконечно малая низшего порядка малости, чем 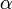 . Соответственно
. Соответственно  .
.
§ Если  (предел конечен и не равен 0), то
(предел конечен и не равен 0), то 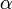 и
и  являются бесконечно малыми величинами одного порядка малости.
являются бесконечно малыми величинами одного порядка малости.
Это обозначается как 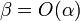 или
или  (в силу симметричности данного отношения).
(в силу симметричности данного отношения).
§ Если  (предел конечен и не равен 0), то бесконечно малая величина
(предел конечен и не равен 0), то бесконечно малая величина  имеет
имеет  -й порядок малости относительно бесконечно малой
-й порядок малости относительно бесконечно малой 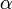 .
.
Для вычисления подобных пределов удобно использовать правило Лопиталя.
[править] Примеры сравнения
§ При  величина
величина  имеет высший порядок малости относительно
имеет высший порядок малости относительно 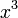 , так как
, так как  . С другой стороны,
. С другой стороны, 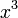 имеет низший порядок малости относительно
имеет низший порядок малости относительно  , так как
, так как  .
.
С использованием О -символики полученные результаты могут быть записаны в следующем виде  .
.
§  то есть при
то есть при  функции
функции 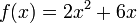 и
и 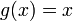 являются бесконечно малыми величинами одного порядка.
являются бесконечно малыми величинами одного порядка.
В данном случае справедливы записи  и
и 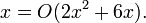
§ При  бесконечно малая величина
бесконечно малая величина 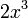 имеет третий порядок малости относительно
имеет третий порядок малости относительно 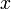 , поскольку
, поскольку  , бесконечно малая
, бесконечно малая  — второй порядок, бесконечно малая
— второй порядок, бесконечно малая 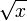 — порядок 0, 5.
— порядок 0, 5.
Следствие 1. Если  и
и  , то
, то  .
.
Следствие 2. Если  и c= const, то
и c= const, то  .
.
Теорема 3. Отношение бесконечно малой функции α (x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.
Доказательство. Пусть 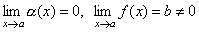 . Тогда 1 /f(x) есть ограниченная функция. Поэтому дробь
. Тогда 1 /f(x) есть ограниченная функция. Поэтому дробь  есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.
есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.
|