
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические упражнения
|
|
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
1) Понятия числовой последовательности и ее предела.
Теорема об ограниченности сходящейся последовательности.
2) Понятие предела функции в точке. Понятие функции, ограниченной в окрестности точки. Теорема об ограниченности функции, имеющей предел.
3) Теорема о переходе к пределу в неравенствах.
4) Теорема о пределе промежуточной функции.
5) Понятие непрерывности функции. Доказать непрерывность функции cosx 
6) Первый замечательный предел 
7) Понятие бесконечно малой функции. Теорема о связи между функцией, ее пределом и бесконечно малой.
8) Теорема о сумме бесконечно малых функций.
9) Теорема о произведении бесконечно малой функции на ограниченную функцию.
10) Теорема об отношении бесконечно малой функции к функции, имеющей предел, отличный от нуля.
11) Теорема о пределе суммы.
12) Теорема о пределе произведения.
13) Теорема о пределе частного.
14) Теорема о переходе к пределу под знаком непрерывной функции.
15) Непрерывность суммы, произведения и частного.
16) Непрерывность сложной функции.
17) Понятие бесконечно большой функции. Теоремы о связи бесконечно больших функций с бесконечно малыми.
18) Сравнение бесконечно малых функций.
19) Эквивалентные бесконечно малые функции. Теорема о замене бесконечно милых функций эквивалентными.
20) Условие эквивалентности бесконечно малых функций.
ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ
1) Доказать, что если  , то
, то 
Вытекает ли из существования  существование
существование  ?
?
Указание. Доказать и использовать неравенство

2) Доказать, что последовательность  расходится.
расходится.
3) Сформулировать на языке «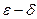 » утверждение: «Число А не является пределом в точке
» утверждение: «Число А не является пределом в точке  функции
функции  , определенной в окрестности точки
, определенной в окрестности точки  ».
».
4)Доказать, что если непрерывная  функция, то
функция, то  есть также непрерывная функция. Верно ли обратное утверждение?
есть также непрерывная функция. Верно ли обратное утверждение?
5) Сформулировать на языке «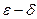 » утверждение:
» утверждение:
«Функция  , определенная в окрестности точки
, определенная в окрестности точки  , не является непрерывной в этой точке».
, не является непрерывной в этой точке».
6) Пусть  ,, а
,, а 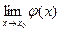 не существует. Доказать что
не существует. Доказать что  не существует.
не существует.
Указание. Допустить противное и использовать теорему о пределе частного.

|
7) Пусть функция  имеет предел в точке
имеет предел в точке  . а функция
. а функция  не имеет предела. Будут ли существовать пределы:
не имеет предела. Будут ли существовать пределы:
а)  ;
;
б)  ?
?
Рассмотреть пример: 
8) Пусть  , а функция
, а функция  бесконечно большая при
бесконечно большая при  . Доказать, что произведение
. Доказать, что произведение  является бесконечно большой функцией при
является бесконечно большой функцией при 
9) Является ли бесконечно большой при  функция
функция  ?
?
10) Пусть  и
и  при
при 
Доказать, что если  не существует, то
не существует, то  тоже не существует.
тоже не существует.