Операции над случайными событиями

СЛУЧАЙНОЕ СОБЫТИЕ И ВЕРОЯТНОСТЬ

Операции над случайными событиями

Комплекс условий, который можно осуществить неограниченное число раз с целью получения некоторого результата, называется испытанием или экспериментом со случайным исходом. Каждый исход случайного эксперимента является элементарным событием и обозначается буквой w. Множество всех несовместных исходов испытания называется пространством элементарных событий W.

Любое подмножество пространства элементарных событий называется случайным событием. Событие, происходящее при каждом осуществлении одного и того же испытания, называется достоверным, оно совпадает с множеством W. Событие, которое не может произойти при данных условиях, называется невозможным, оно не содержит ни одного исхода w, представляя собой пустое множество, и обозначается Æ.

Для случайных событий определены следующие операции и отношения:

А Ì В - отношение включения: множество А является подмножеством множества В - событие А влечет за собой событие В (рис. 1.1, а);

А = В - отношение эквивалентности - событие А тождественно событию В (А Ì В и В Ì А одновременно);

А + В - объединение множеств - сумма событий - состоит в том, что в результате испытания произойдет хотя бы одно из событий А или В (рис. 1.1, б);

А В - пересечение множеств - произведение событий - состоит в одновременном (совместном) появлении событий А и В (рис. 1.1, в);

А - В - разность событий - означает, что событие А произошло, а событие В не произошло (рис. 1.1, г);

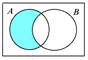
а) А Ì В б) А + В в) АВ г) А - В

Рис. 1.1

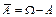- дополнение множества А до W - событие, противоположное событию А, состоит в том, что в результате испытания событие А не произойдет (рис. 1.2, а).

События A и B несовместны, если AB = Æ (рис. 1.2, б). События A ₁, A ₂ ,..., A_n попарно несовместны, еcли для всех i ¹ j, где i = 1,..., n, j = 1,..., n, выполняется условие A_i A_j = Æ. События A ₁, A ₂ ,..., A_n, удовлетворяющие условию составляют полную группу событий. Если при этом A_i A_j = = Æ, такая совокупность составляет полную группу несовместных событий.

Операции сложения и умножения событий обладают следующими свойствами:

а) А + В = В + А, АВ = ВА (коммутативность сложения и умножения);

б) (А + В) + С = А + (В + С);

(АВ) С = А (ВС) (ассоциативность сложения и умножения);

Рис. 1.2

в) (А + В) С = АС + ВС (дистрибутивность умножения относительно сложения);

г) А + Æ = А; А W = А;

д) А + = W; А = Æ;

е) .

1.1. Игральная кость бросается дважды. Требуется описать: 1) пространство элементарных событий W; 2) событие A, состоящее в том, что сумма выпавших очков четная; 3) событие B, состоящее в том, что первое выпавшее число четное; 4) A + B; 5) A-B, B - A; 6) AB; 7) , .

¢ 1. Каждому из шести исходов при первом бросании кости соответствует 6 возможных исходов при втором бросании. Следовательно, пространство элементарных событий W имеет вид

W = {(1; 1), (1; 2),..., (1; 6), (2; 1),...(2; 6),..., (6; 1), (6; 2),..., (6; 6)} и содержит 6 × 6=36 элементарных событий.

2. Событие A состоит из тех элементарных событий, у которых результаты обоих бросаний либо четные, либо нечетные:

A = {(1; 1), (1; 3), (1; 5), (2; 2), (2; 4), (2; 6), (3; 1),..., (6; 6)}. Нетрудно видеть, что A содержит 18 элементарных событий.

3. Событие B содержит те элементы пространства W, у которых первые цифры четные, вторые – любые:

В = {(2; 1), (2; 2), (2; 3),..., (4; 1), (4; 2),...(6; 1),..., (6; 6)} - всего 18 исходов.

4. Событие A + B состоит в том, что при двукратном бросании игральной кости сумма выпавших очков четная или первое выпавшее число четное. Иными словами, требуется найти объединение множеств A и B, для чего множество исходов одного из них следует дополнить недостающими исходами другого. В результате получим множество, состоящее из 27 элементарных событий:

A+B = { (1; 1), (1; 3), (1; 5), (2; 1), (2; 2),..., (6; 5), (6; 6) }.

5. Чтобы получить разность A-B, следует из множества исходов A исключить исходы, входящие в B. Аналогично получается разность B - A.

6. Произведением A× B является множество тех элементарных событий, которые принадлежат множествам A и B одновременно:

AB = {(2; 2), (2; 4), (2; 6), (4; 2),..., (6; 4), (6; 6)} - всего 9 исходов.

7. Для описания и достаточно вспомнить, что

= W- A, = W- B. £

1.2. Доказать справедливость следующих тождеств:

а) б) в)

¢ а) Известно, что А W = А и А + = W, а на основании свойств (а) и (е) ; тогда

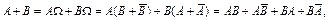
откуда

б) Из свойства (д) следует, что 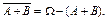Рассмотрим сумму событий Так как то

Отсюда следует, что .

в) Из доказательства предыдущего тождества следует, что

откуда .

Так как

£

В задачах 1.3 - 1.6 доказать справедливость следующих тождеств:

1.3.

1.4.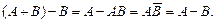

Эти равенства свидетельствуют о том, что «приведение подобных членов» в алгебре событий недопустимо.

1.5. - дистрибутивность сложения относительно умножения.

1.6.

1.7. Показать, что если то выполняются соотношения

1.8. Показать, что если то выполняется соотношение

Доказать тождества:

1.9.

1.10.

1.11.

Пусть А, В, С - три случайных события, которые могут появиться в данном эксперименте.Выразить указанные ниже события в алгебре событий А, В, С.

1.12. = {из трех событий А, В, С произойдет ровно одно};

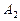= {из трех событий А, В, С произойдет ровно два}.

1.13. = {из трех событий А, В, С произойдет хотя бы одно};

= {из трех событий А, В, С произойдет не меньше двух}.

1.14. = {из трех событий А, В, С не произойдет ни одного};

= {из трех событий А, В, С произойдет хотя бы два};

= {из трех событий А, В, С не произойдет хотя бы одно}.

Рис. 1.1 Рис. 1.2

1.15. Электрическая цепь составлена по схеме, приведенной на рис. 1.1. Событие = {элемент с номером k вышел из строя}, Событие В = {разрыв цепи.}. Выразить событие В в алгебре событий

1.16. Электрическая цепь составлена по схеме, приведенной на рис. 1.2. Событие = {элемент с номером k вышел из строя}, 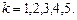Событие В = {разрыв цепи. }. Выразить событие В в алгебре событий

1.17. Даны два случайных события А и В. Доказать, что 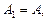образуют полную группу несовместных событий.